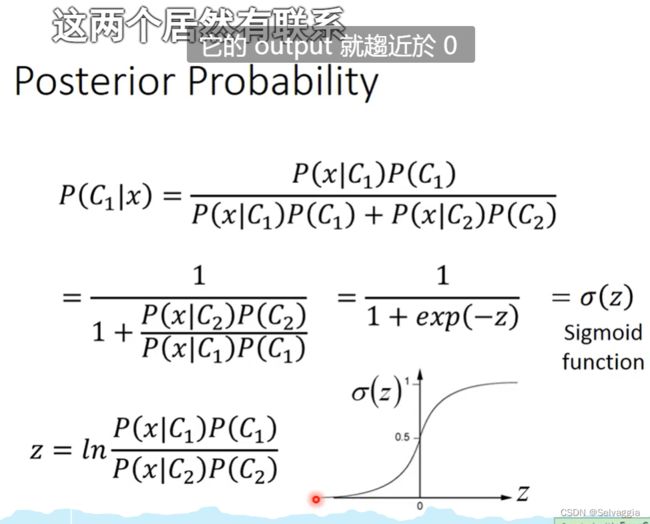
预测宝可梦武力值、分类宝可梦
regression case
股票预测
无人车看到的各种sensor
影像镜头看到马路上的东西作为输入,输出就是方向盘角度等等的操纵策略
scalar 标量
这个是热力图,相当于你的XYZ但是Z用颜色表示了
closed-form solution 闭合解
learning rate事先定好的数值
在linear regression上没有local optimal
一般性 泛化性
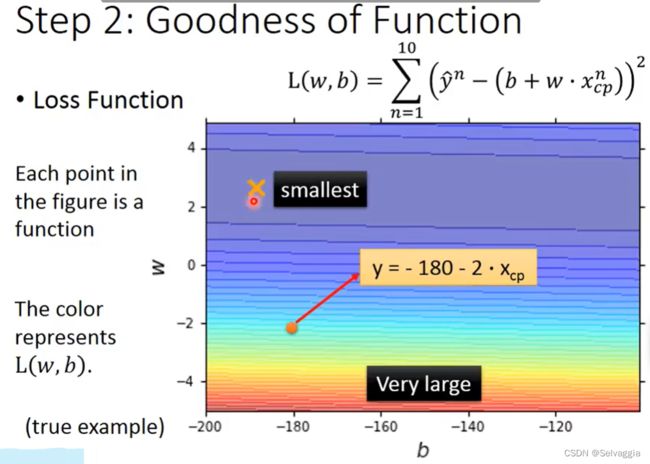
来自于random的数值,进化值某个方面受random值的影响
training error太小,training结果太好就可能出现overfitting的情况
博士根据常识改变model,删掉某个已知不影响的参数,可能还有其他比较关键有影响力的factor
参数越小越接近0,可以达到更平滑的效果,input改变,output不那么敏感,受影响程度不大
为什么喜欢平滑
用L2范数正则化,即岭回归
惩罚项
平滑,output对输入不敏感,输入被杂讯干扰,受到比较小的影响
我可以理解为岭回归有一定的抗噪声的能力吗
太平滑是一条水平线,也什么都干不成,太平滑结果又会变差
调参侠
bw都是常数,只有w受x影响,bias不影响平滑程度
这边就是adamW优化器不对bias做decay的原因,因为它就相对于正则化
classification分类
gaussian distribution 高斯分布==正态分布
硬解

强制按照regression来训练
以0为分界
大于0表示1,
太大超过1不行,远大于1的点是错误error
太小不行
分界线会考虑到偏离较远的点而偏离最合适的位置,让他们尽可能不变成距离分界线很远的错误的点
为了减小loss而不符常理,最小二乘的弊端
regression会惩罚那些太过正确,output太大的那些值
把每一类当作一个数字,但是数字之间有关系,类别之间不一定和数字之间的关系保持一致比如大小,是否相邻
binary classification
如何确定比较好的loss function
分类错误的次数
不能微分,无法用gradient decent
SVM,perceptron
计算某个x出现的机率,可以得知x的distributtion分布,就可以自己产生x
要把18种都分类正确,做不太出来
因为有些数值接近,但是却不是一个系的
每个宝可梦用个向量来表示,他的各种特征
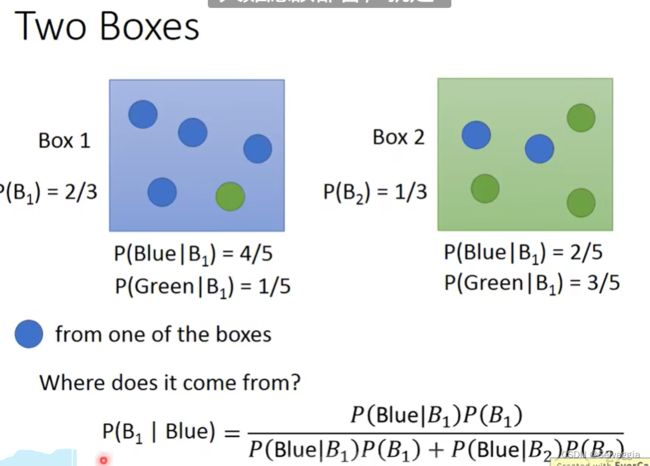
水系里面挑一只出来是海龟的概率
是从高斯分布里面sample出来的,sample了79个,
不同的μ和Σ,分布的最高点是不一样的
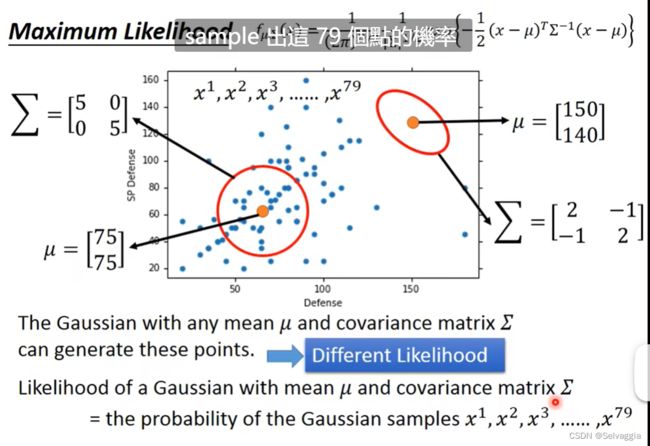
这个完全是从统计学的角度来做分类了
可以理解为由样本生成高斯分布,再用海龟的数据去找到在高斯分布的位置
散点来推测密度函数:极大似然估计
每个高斯都有可能sample出所有的79个点,但是 sample出79个点的可能性是不同的
每个点被独立sample出来的,机率独立相乘
找出一个Gaussian,sample出这79个点的概率是最大的
likelihood最大
取微分以下找极值
最大似然估计!!
mean和variance通过最大似然分别求微分偏导得到
每个宝可梦用个向量来表示,他的各种特
热力图怎么做出来的,所有平面上的点全都代入一遍两个高斯么?
机器学习可以在高维空间处理问题,在七维空间上说不定 重叠在boundary上的样本点是分开的,分界线boundary更加的明显,每个宝可梦通过七个数字的向量来表示feature
covariance matrix 协方差矩阵!!!
不同的class可以share同一个covariance matrix
和input的feature size的平方成正比
feature size很大的时候,covariance matrix增长很快
如果把2个不同的Gaussian都给不同的covariance matrix ,model的参数可能太多了,参数一朵,variance(方差)就大,容易overfitting
为了减小参数,描述这两个类的feature分布的Gaussian,故意给他们相同的 covariance matrix
强制共用同一组 covariance matrix
为了减少model复杂度,共用一个协方差矩阵,使得概率密度分布的散布程度在class1和class2的分布上是一样的
这时就要同时基于c1和c2的样本概率去求两个分布各自的均值和共同的协方差矩阵
为减少模型复杂度,去共用一个协方差而不是共用一个均值,因为显然class1和class2在特征分布图上有不同的几何中心,而modify散布程度的自由性更大
bishop指的是Bishop - Pattern Recognition And Machine Learning
把原来两个Gaussian各自算的covariance matrix加权平均,得到强制要求用共同的Gaussian时对应的所得到的covariance matrix
就是一种加权平均的策略,权重根据个数来设定被,你可以换成均值之类的都可以的
均值比方差更能代表 两组 之间的 差异 方差主要是显示组内差异
使用共同的covariance matrix之后,the boundary变成了linear的

在高维空间中,分类的准确率大大提高了
人没办法知道机器在运作中的复杂缠绕的机理
没有什么原理,就是纯工程上觉得it just works
二维feature很少,人一看就知道,分界线和分类的好坏
个人理解共用协方差只是为了减小模型的复杂度,这只是在基于自己决定好model结构的基础上去优化一下model,从而获得model在分布上有更小的误差
结果是很trivial的
选别的几率模型
简单模型,参数比较少,bias小,variance大
复杂的模型对应相反
binary feature ,说使用Gaussian模型机率 分布产生的,不太合理
这时可能会选择用 Bernoulli distributions 伯努利分布
伯努利分布Ber-n,n=1,其实就是0-1分布
inner product:数量积,内积