数据挖掘之时间序列模型（最全流程分析）

美股封盘(close)数据
获取数据源—>缺失值处理—>检验数据稳定性—>序列平稳—>参数寻优—>建立模型—>模型检验—>模型预测

一、获取数据源

#以谷歌美股封盘数据来构建时间序列模型|导入库包
from pandas_datareader import data
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf 
from statsmodels.tsa.arima_model import ARIMA
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")

#设置股票代码与起始时间
stock_code = "GOOG"
start_date = "2005-01-01"
end_date = "2019-12-25"
stock_info = data.get_data_yahoo(stock_code, start_date, end_date)
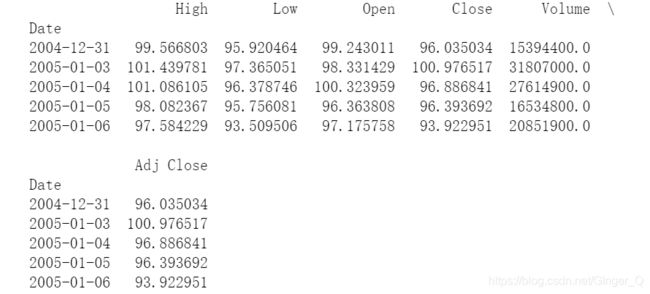
#展示前5行股票数据
print(stock_info.head())
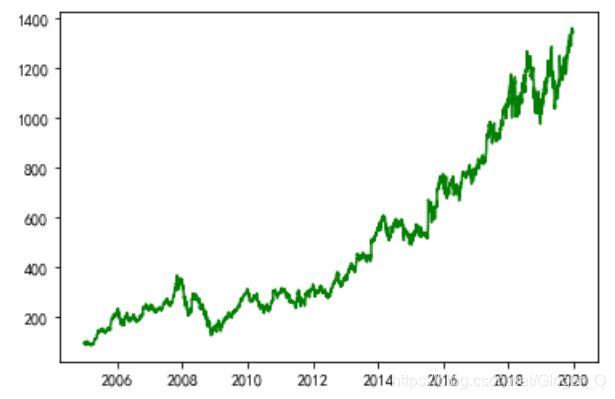
plt.plot(stock_info['Close'], 'g') #展示数据图
plt.show()

展示数据图

图描述

#获取封盘数据
df = pd.DataFrame(data=stock_info)
data = df.loc[:,['Close']]
data.tail() #查看数据截止日期

二、缺失值处理

没有的话，手动创造一些缺失值

1.先对数据进行降采样

2.然后对数据进行升采样

3.之后使用向前填充、向后填充、线性填充来进行缺失值的处理

在处理数据时也可以用降升采样,在这里我是造一些缺失值

#降采样
data1 = data.resample('2W').mean() #取三天的平均值
data1.head()

#查看数据个数
n_sample = data1.shape[0]
n_sample

392

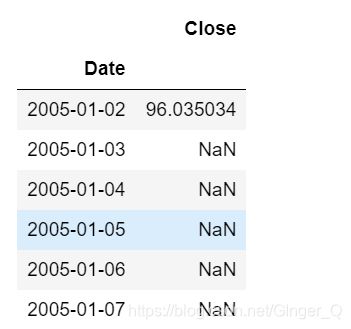
#升采样
data2 = data1.resample('D').asfreq()
data2.head(6)

#缺失值处理 分别为ffill（取前面的值）、bfill（取后面的值）、interpolate(线性取值)
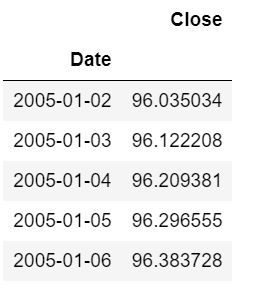
#这里采取的线性填充
data3 = data2.resample('D').interpolate()
data3.head()

三、检验序列的稳定性

主要是观察数据是否是平稳序列，如果不是则要进行处理转换为平稳序列

data = data['Close'].resample('W-MON').mean() #用的是降采样后的数据
data_train = data['2005':'2017'] #将2005-2017的数据化为测试集

#画出测试集数据图
data_train.plot(figsize=(8,4))
plt.legend(bbox_to_anchor=(1.25,0.5))
plt.title('Close')
sns.despine()

#观察法

# 移动平均图
def draw_trend(timeseries, size):
    f = plt.figure(figsize=(8,4),facecolor='white')
    # 对size个数据进行移动平均
    rol_mean = timeseries.rolling(window=size).mean()
    # 对size个数据移动平均的方差
    rol_std = timeseries.rolling(window=size).std()
 
    timeseries.plot(color='blue', label='Original')
    rol_mean.plot(color='red', label='Rolling Mean')
    rol_std.plot(color='black', label='Rolling standard deviation')
    plt.legend(loc='best')
    plt.title('Rolling Mean & Standard Deviation')
    plt.show()
draw_trend(data_train,12) #移动平均图

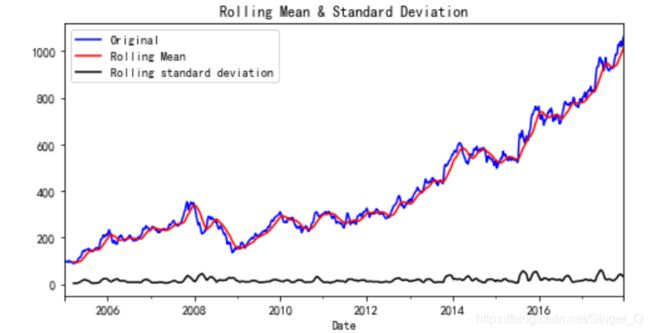
通过上图，我们可以发现数据的移动平均值是不稳定的,呈上升趋势。接下来我们再看单位根检验法。

#单位根检验法
#Dickey-Fuller test:
from statsmodels.tsa.stattools import adfuller
def teststationarity(data_train):
    dftest = adfuller(data_train)
    # 对上述函数求得的值进行语义描述
    dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
    for key,value in dftest[4].items():
        dfoutput['Critical Value (%s)'%key] = value
    return dfoutput
print(teststationarity(data_train))

p值远大于0.05 序列不稳定

四、序列平稳化

# 差分运算
#除个别离群值,序列趋于平稳
data_diff = data_train.diff()
data_diff = data_diff.dropna() # 差分后需要排空，

plt.rcParams['font.sans-serif'] = ['SimHei'] #显示中文字体
plt.rcParams['axes.unicode_minus'] = False   #显示负号

plt.figure(figsize=(12,4))#画出差分图
data_diff.plot()
plt.title('一阶差分')
plt.show()   

再次检验

teststationarity(data_diff)

p值小于0.05 而且检验值同时小于99%，95%，90%置信区间下的临界的ADF检验的值
序列为平稳

五、参数寻优

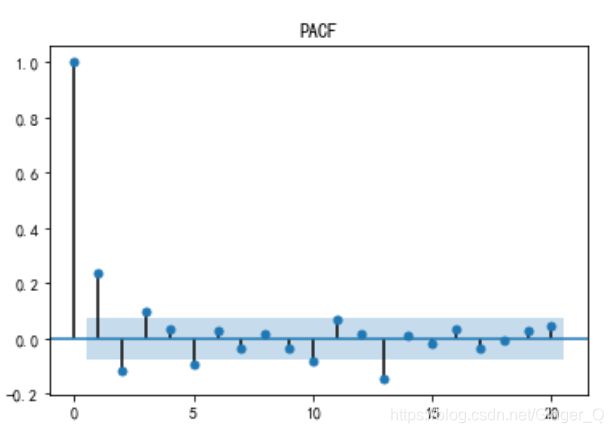
#画出差分后acf,pacf图
plt.figure(figsize=(6,2))
acf = plot_acf(data_diff,lags=20)
plt.title('ACF')
acf.show()

plt.figure(figsize=(6,2))
pacf = plot_pacf(data_diff,lags=20)
plt.title('PACF')
pacf.show()

由acf图截尾可以得q为1,1阶之后点都在置信区间范围内

由pacf图截尾可以p为5,5阶之后点都在置信区间范围内

六、建立模型

#寻找最优参数pq
#通过导入import itertools来遍历 p属于[0 ,10]，q属于[0, 2] d=1
import itertools

p_min = 0
d_min = 1
q_min = 0
p_max = 5
d_max = 1
q_max = 5

# 初始化数据框以存储结果
results_bic = pd.DataFrame(
    index=['AR{}'.format(i) for i in range(p_min, p_max + 1)],
    columns=['MA{}'.format(i) for i in range(q_min, q_max + 1)])

for p, d, q in itertools.product(
        range(p_min, p_max + 1), range(d_min, d_max + 1),
        range(q_min, q_max + 1)):
    if p == 0 and d == 0 and q == 0:
        results_bic.loc['AR{}'.format(p), 'MA{}'.format(q)] = np.nan
        continue
    try:
        model = sm.tsa.SARIMAX(
            data_train,
            order=(p, d, q),
        )
        results = model.fit()
        results_bic.loc['AR{}'.format(p), 'MA{}'.format(q)] = results.bic
    except:
        continue
results_bic = results_bic[results_bic.columns].astype(float)


#画出BIC热力图
fig, ax = plt.subplots(figsize=(12, 8))
ax = sns.heatmap(results_bic,
                 mask=results_bic.isnull(),
                 ax=ax,
                 annot=True,
                 fmt='.2f',
                 );
ax.set_title('BIC')

#获取最优参数

train_results = sm.tsa.arma_order_select_ic(
    data_train, ic=['aic', 'bic'], trend='nc', max_ar=5, max_ma=5)

print('AIC', train_results.aic_min_order)
print('BIC', train_results.bic_min_order)

七、模型检验

由于ACF.PACF确定的pq值与BIC.AIC检验的结果不一样

1.(5,1,1)

2.(1,1,1)

3.(5,1,4)

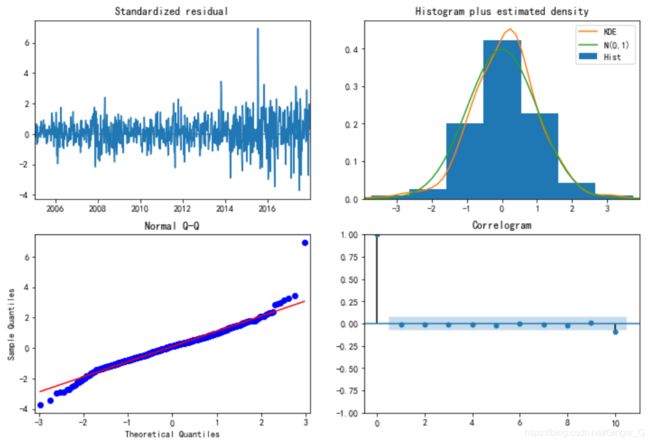
#画出残差图,正态分布图,QQ图,相关图的检验图
arima511= sm.tsa.SARIMAX(data_train, order=(5,1,1))
model_results511 = arima511.fit(disp=True)
arima111= sm.tsa.SARIMAX(data_train, order=(1,1,1))
model_results111 = arima111.fit(disp=True)
arima313= sm.tsa.SARIMAX(data_train, order=(5,1,4))
model_results313 = arima313.fit(disp=True)
model_results511.plot_diagnostics(figsize=(12, 8));
model_results111.plot_diagnostics(figsize=(12, 8));
model_results313.plot_diagnostics(figsize=(12, 8));

通过残差图,qq图以及相关图最终确定参数为(5,1,1)

八、模型预测

model = ARIMA(data_train,order=(5,1,4),freq='W-MON') #设置模型
result = model.fit()  #训练模型
pre = result.predict('2017-09','2018-09',dynamic=True,typ='levels')  #带入预测时间区域
plt.figure(figsize=(12,6))
plt.plot(pre)
plt.plot(data_train) #画出预测图

预测为上升趋势 。