维诺图（Voronoi diagram）学习笔记及相关思考

   本篇博客主要记录在学习维诺图（Voronoi diagram）过程中的笔记及相关思考和概括总结

一、主要参考资料
     1、维诺图（Voronoi Diagram）分析与实现：【点击此处跳转】
     2、维诺图（Voronoi 图）：【点击此处跳转】
     3、百度百科-泰森多边形：【点击此处跳转】
     4、德劳内(delaunay)三角网的生成算法：【点击此处跳转】

---

二、维诺图（Voronoi diagram）简介

     维诺图（Voronoi diagram），又称泰森多边形（Thiessen polygon）、沃罗诺伊图（Voronoi diagram）、狄利克雷镶嵌（Dirichlet tessellation）、冯洛诺伊图 等

     维诺图是由一组由连接两邻点直线的垂直平分线组成的连续多边形组成。具备以下特点：
     （1）维诺图把平面划分成n个多边形域，每个多边形内 只有 一个生成元；
    （2）每个多边形内的点到该生成元距离短于到其它生成元距离；
    （3）多边形边界上的点到生成此边界的两个生成元的距离相等；
    （4）邻接图形的Voronoi多边形界线以原邻接界线作为子集。
    （5）Voronoi图至多有2 * n - 5个顶点和3 * n - 6条边。
    （6）多边形内的生成元是形成三边的三点构成的三角形的外界圆圆心，而且所有的这些外界圆内部不含任何除这三点之外的顶点（空心圆特性）。

二、维诺图的生成步骤

     首先，将离散点构成德洛内三角网（Delaunay三角网），并对离散点和形成的三角形编号，记录每个三角形是由哪三个离散点构成的。 然后 ，计算并记录每个三角形的外接圆圆心，最后，遍历三角形链表，寻找与当前三角形pTri三边共边的相邻三角形TriA，TriB和TriC。如果找到，则把寻找到的三角形的外心与pTri的外心连接，存入维诺边链表中。如果找不到，说明没有与该边相邻的三角形，即该边是德洛内三角网最外侧的便，则求出该边的中垂线射线存入维诺边链表中。遍历结束后，所有维诺边被找到，根据边画出维诺图。

三、德洛内三角网（Delaunay三角网）

    1、Delaunay三角网的特性

    （1）空圆性：任意一个三角形的外接圆内部不包含其他点，这个特征已经作为创建德洛内(Delaunay) 三角网的一项判别标准。

    （2）最大最小角性质：在由点集所构成的三角网中，Delaunay三角网中三角形的最小角度是最大的，且每两个相邻的三角形构成的凸四边形的对角线，在相互交换后，六个内角的最小角不再增大。

    （3）最接近：以最近临的三点形成三角形，且三角形的边皆不相交。

    （4）唯一性：不论从区域何处开始构建，最终都将得到一致的结果，也就是说Delaunay三角网是唯一的。

    （5）最规则：如果将三角网中的每个三角形的最小角进行升序排列，则Delaunay三角网的排列得到的数值最大。

    （6）区域性：新增、删除、移动某一个顶点时只会影响临近的三角形。

    （7）具有凸多边形的外壳：三角网最外层的边界形成一个凸多边形的外壳。

    Delaunay 三角网的优点是结构良好, 数据结构简单, 数据冗余度小, 存储效率高, 与不规则的地面特征和谐一致,可以表示线性特征和迭加任意形状的区域边界, 易于更新,可适应各种分布密度的数据等; 它的局限性是, 算法实现比较复杂和困难, 但已经有了较多成熟的实现算法。

    Delaunay 三角网是Voronoi图的伴生图形, 它们两个是被普遍接受和采用的 分析研究区域离散数据的有力工具。它是通过连接具有公共顶点的三个V n多边形的生长中心而生成的, 这个公共顶点就是形成的Delaunay三角形外接圆的圆心。

    2、Delaunay三角网的生成算法

    常见的Delaunay三角网生成算法主要有角度判别法、逐点插入法、分治法

    （1）角度判别法

     首先，从点集S中任选一点作为起点p1，寻找与其距离最近的点作为第二点p2。创建一个空队列Q来存储扩展边。并将边p1−>p2存入队列Q完成初始化。

     然后循环从Q中取边并进行三角网的生长，第一次循环时取出的边即为p1−>p2，在边p1−>p2的右侧找到扩展点p3，在边p2−>p1的右侧找到扩展点p4，记录扩展得到的两个三角形（扩展失败则不记录）。将边p1−>p3、p3−>p2、p2−>p4和p4−>p1加入队列Q（扩展失败的边不加入队列）(找拓展点的方法为，在连线的右侧寻找与其构成最大夹角的第三点，若其右侧没有满足条件的点，则这条边扩展失败)。

     从队列Q中删除边p1−>p2，本次拓展结束，进行下一次循环，直至队列Q为空，算法结束。

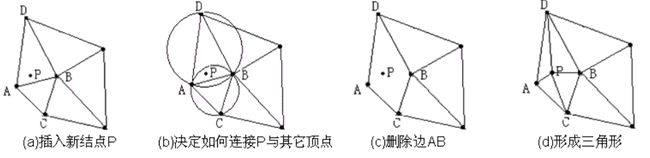
    （2）逐点插入法

     这里仅介绍逐点插入法主要思路，此部分内容参考资料4中介绍的较为详细

     （1）构造一个超级三角形，包含所有散点，放入三角形链表。

     （2）将点集S中的散点依次插入超级三角形，在三角形链表中找出其外接圆包含插入点的三角形（称为该点的影响三角形），删除影响三角形的公共边，并将插入点同影响三角形的全部顶点连接起来，从而完成一个点在Delaunay三角形链表中的插入。

     （3）根据优化准则对局部新形成的三角形进行优化。将形成的三角形放入Delaunay三角形链表。

     （4）循环执行上述第2步，直到所有散点插入完毕。

     上述步骤3的局部优化的准则指的是：对新形成的三角形进行优化，将两个具有共同边的三角形合成一个多边形，以最大空圆准则作检查其第四个顶点是否在三角形的外接圆之内。如果在，修正对角线即将对角线对调，即完成局部优化过程的处理。

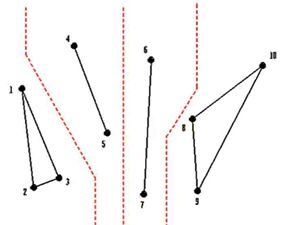
    （3）分治法

     分治法的主要思路是将点集S中所有点按照x坐标的升序进行排序，x坐标相同时，按照y坐标进行排序，接着将整个点集递归地划分数量相近的两个子集，直到子集中点的数目小于等于3，。

     对于一条边，如果它的两个端点都在分割线的左边，称它为LL边，一端在左边一端在右边称为LR边，两个端点都在右边称为RR边，分治法的重点在于如何递归地合并三角网格，先确定一条LR边，然后按照最大最小角特性分别在分治线的左右两侧寻找候选点，然后按照空圆性确定新生成的三角形，详情见参考资料2