LeetCode刷题碎碎念(四):Graph
LeetCode刷题碎碎念(四):Graph
-
- Graph
-
- Queue + Hashtable
-
- 133. Clone Graph (Medium)
- 138. Copy List with Random Pointer (Medium)
- Grid + Connected Components
-
- 200. Number of Islands (Medium)
- 547. Friend Circles (Medium)
- 695. Max Area of Island (Medium)
- 733. Flood Fill (Easy)
- DFS + Connected Components
-
- 841. Keys and Rooms (Medium)
- 1202. Smallest String With Swaps (Medium)
- Topology Sorting
-
- 207. Course Schedule (Medium)
- 210. Course Schedule II (Medium)
- 802. Find Eventual Safe States (Medium)
- Union Find
-
- 399. Evaluate Division (Medium)
- 721. Accounts Merge (Medium)
- 737. Sentence Similarity II (Medium)
- Bipartition & Graph coloring
-
- 785. Is Graph Bipartite? (Medium)
- 886. Possible Bipartition (Medium)
- 1042. Flower Planting With No Adjacent (Easy)
- In/Out Degrees
-
- 997. Find the Town Judge (Easy)
- Unweighted Shortest Path / BFS
-
- 433. Minimum Genetic Mutation (Medium)
- 863. All Nodes Distance K in Binary Tree (Medium)
- 1129. Shortest Path with Alternating Colors (Medium)
Graph
Queue + Hashtable
133. Clone Graph (Medium)
克隆一个无向图。
Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
map:在map中储存新的克隆节点和原始节点的关系。
queue:还没有克隆过的节点,初始0节点,把节点的neighbor都加入。
- 克隆每一个节点
- 连接节点
example: input [ [1, 2], [0,2], [0,1,2] ]
curr queue map
0 0 - > null
0 1 2 0 -> 0’, 1 -> null, 2 -> null
1 2 0 -> 0’, 1 -> 1’, 2 -> null
2 empty 0 -> 0’, 1 -> 1’, 2 -> 2’
之后构建新节点之间的连接。
Solution 1 DFS:
# DFS
def __init__(self):
self.visited = {}
def cloneGraph(self, node: 'Node') -> 'Node':
if not node:
return node
if node in self.visited:
return self.visited[node]
# Create a clone for the given node.
# Note that we don't have cloned neighbors as of now, hence [].
clone_node = Node(node.val, [])
# map from original node to clone node
self.visited[node] = clone_node
if node.neighbors:
clone_node.neighbors = [self.cloneGraph(n) for n in node.neighbors]
return clone_node
Solution 2 BFS:
# BFS
def cloneGraph(self, node: 'Node') -> 'Node':
visited = {}
if not node:
return node
queue = deque([node])
visited[node] = Node(node.val, [])
while queue:
n = queue.popleft()
for neighbor in n.neighbors:
if neighbor not in visited:
# Clone the neighbor and put in the visited, if not present already
visited[neighbor] = Node(neighbor.val, [])
# Add the newly encountered node to the queue.
queue.append(neighbor)
# Add the clone of the neighbor to the neighbors of the clone node "n".
visited[n].neighbors.append(visited[neighbor])
# Return the clone of the node from visited.
return visited[node]
138. Copy List with Random Pointer (Medium)
A linked list is given such that each node contains an additional random pointer which could point to any node in the list or null.
Return a deep copy of the list.
The Linked List is represented in the input/output as a list of n nodes. Each node is represented as a pair of [val, random_index] where:
val: an integer representing Node.val
random_index: the index of the node (range from 0 to n-1) where random pointer points to, or null if it does not point to any node.
每个点有两个指针,一个指向下一个点,一个指向随机点或者null。

Python Node:
https://www.tutorialspoint.com/python/python_nodes.htm
Creation of Nodes:
class daynames:
def __init__(self, dataval=None):
self.dataval = dataval
self.nextval = None
e1 = daynames('Mon')
e2 = daynames('Tue')
e3 = daynames('Wed')
e1.nextval = e3
e3.nextval = e2
Traversing the Node Elements:
class daynames:
def __init__(self, dataval=None):
self.dataval = dataval
self.nextval = None
e1 = daynames('Mon')
e2 = daynames('Wed')
e3 = daynames('Tue')
e4 = daynames('Thu')
e1.nextval = e3
e3.nextval = e2
e2.nextval = e4
thisvalue = e1
while thisvalue:
print(thisvalue.dataval)
thisvalue = thisvalue.nextval
Solution 1 Recursive:
"""
# Definition for a Node.
class Node:
def __init__(self, x: int, next: 'Node' = None, random: 'Node' = None):
self.val = int(x)
self.next = next
self.random = random
"""
class Solution:
# Recursive
def __init__(self):\
# dict: old nodes as keys and new nodes as values
self.visitedHash = {}
def copyRandomList(self, head: 'Node') -> 'Node':
if head == None:
return None
# if current node already processed, return its clone version
if head in self.visitedHash:
return self.visitedHash[head]
node = Node(head.val, None, None) # using 'class Node' to creat a new node with value same as old node
self.visitedHash[head] = node # save this value in hashmap
node.next = self.copyRandomList(head.next)
node.random = self.copyRandomList(head.random)
return node
Solution 2 Iteration:
# Iteration
def __init__(self):\
# dict: old nodes as keys and new nodes as values
self.visited = {}
def getCloneNode(self, node):
if node:
if node in self.visited:
return self.visited[node]
else: # create a new node, save the reference in the visited dictionary and return it.
self.visited[node] = Node(node.val, None, None)
return self.visited[node]
return None
def copyRandomList(self, head: 'Node') -> 'Node':
if not head:
return head
old_node = head
new_node = Node(old_node.val, None, None)
self.visited[old_node] = new_node
# Iterate on the linked list until all nodes are cloned.
while old_node != None:
# Get the clones of the nodes referenced by random and next pointers.
new_node.random = self.getCloneNode(old_node.random)
new_node.next = self.getCloneNode(old_node.next)
# Move one step ahead in the linked list.
old_node = old_node.next
new_node = new_node.next
return self.visited[head]
Grid + Connected Components
200. Number of Islands (Medium)
Given a 2d grid map of '1’s (land) and '0’s (water), count the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
Example 1:
Input: grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”] ]
Output: 1

找到1和其相连通的所有1,然后把他们全变成0.
DFS:
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
if not grid: return 0
m = len(grid)
n = len(grid[0])
ans = 0
# 找到一个1,就用dfs把整个岛都找出来,然后抹平变0
# 然后再找下一个1,新的岛,计数+1,再抹平......
for y in range(m):
for x in range(n):
if grid[y][x] == '1':
ans += 1
self.dfs(grid, x, y, n, m)
return ans
def dfs(self, grid, x, y, n, m):
if x < 0 or y < 0 or x >= n or y >= m or grid[y][x] == '0':
# 当超出边界或者只有‘0’->相连1已经找完:结束dfs->该小岛已经全部变成水
return
# 通过dfs,把和grid[y][x]相连的所有1都变成0
grid[y][x] = '0'
# 上下左右寻找
self.dfs(grid, x + 1, y, n, m)
self.dfs(grid, x - 1, y, n, m)
self.dfs(grid, x, y + 1, n, m)
self.dfs(grid, x, y - 1, n, m)
547. Friend Circles (Medium)
If A is a direct friend of B, and B is a direct friend of C, then A is an indirect friend of C. And we defined a friend circle is a group of students who are direct or indirect friends.
Given a NN matrix M representing the friend relationship between students in the class. If M[i][j] = 1, then the ith and jth students are direct friends with each other, otherwise not. And you have to output the total number of friend circles among all the students.
Example 1:
Input:
[[1,1,0],
[1,1,0],
[0,0,1]]
Output: 2
Explanation:The 0th and 1st students are direct friends, so they are in a friend circle.
The 2nd student himself is in a friend circle. So return 2.*
跟上一题基本一样,就是由于direct friend的互相性,M[i][i] = 1 for all students. If M[i][j] = 1, then M[j][i] = 1.
def findCircleNum(self, M: List[List[int]]) -> int:
n = len(M)
ans = 0
for i in range(n):
if M[i][i] == 1: # 寻找还没有被置0的学生
ans += 1
self.dfs(M, i, n) # 寻找他的所有朋友
return ans
def dfs(self, M, curr, n):
for i in range(n): # 遍历全班n个学生
if M[curr][i] == 1: # 谁是他的朋友?
M[curr][i] = M[i][curr] = 0 # 断掉这个朋友连线
self.dfs(M, i, n)
695. Max Area of Island (Medium)
Given a non-empty 2D array grid of 0’s and 1’s, an island is a group of 1’s (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.
Find the maximum area of an island in the given 2D array. (If there is no island, the maximum area is 0.)
Example 1:
[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]
Given the above grid, return 6. Note the answer is not 11, because the island must be connected 4-directionally.
class Solution:
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
def dfs(i, j):
if 0 <= i < m and 0 <= j < n and grid[i][j]:
grid[i][j] = 0
return 1 + dfs(i - 1, j) + dfs(i, j + 1) + dfs(i + 1, j) + dfs(i, j - 1)
return 0
areas = [dfs(i, j) for i in range(m) for j in range(n) if grid[i][j]]
return max(areas) if areas else 0
733. Flood Fill (Easy)
An image is represented by a 2-D array of integers, each integer representing the pixel value of the image (from 0 to 65535).
Given a coordinate (sr, sc) representing the starting pixel (row and column) of the flood fill, and a pixel value newColor, “flood fill” the image.
To perform a “flood fill”, consider the starting pixel, plus any pixels connected 4-directionally to the starting pixel of the same color as the starting pixel, plus any pixels connected 4-directionally to those pixels (also with the same color as the starting pixel), and so on. Replace the color of all of the aforementioned pixels with the newColor.
At the end, return the modified image.
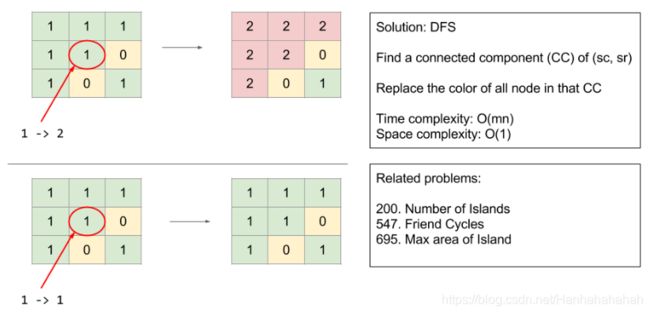
def floodFill(self, image: List[List[int]], sr: int, sc: int, newColor: int) -> List[List[int]]:
if image[sr][sc] == newColor: return image # 初始颜色和新颜色相同,不需要操作
m = len(image)
n = len(image[0])
self.flood(image, sc, sr, n, m, image[sr][sc], newColor)
return image
def flood(self, image, x, y, n, m, orgColor, newColor):
if x < 0 or x >= n or y < 0 or y >= m:
return # 退出
if image[y][x] != orgColor: # 不连通
return
image[y][x] = newColor
self.flood(image, x + 1, y, n, m, orgColor, newColor)
self.flood(image, x - 1, y, n, m, orgColor, newColor)
self.flood(image, x, y + 1, n, m, orgColor, newColor)
self.flood(image, x, y - 1, n, m, orgColor, newColor)
DFS + Connected Components
841. Keys and Rooms (Medium)
Formally, each room i has a list of keys rooms[i], and each key rooms[i][j] is an integer in [0, 1, …, N-1] where N = rooms.length. A key rooms[i][j] = v opens the room v.
Return true if and only if you can enter every room.
Example 1:
Input: [[1],[2],[3],[]]
Output: true
Explanation:
We start in room 0, and pick up key 1. We then go to room 1, and pick up key 2. We then go to room 2, and pick up key 3. We then go to room 3. Since we were able to go to every room, we return true.
Example 2:
Input: [[1,3],[3,0,1],[2],[0]]
Output: false
Explanation: We can’t enter the room with number 2.
class Solution:
def canVisitAllRooms(self, rooms: List[List[int]]) -> bool:
visited = []
self.dfs(rooms, 0, visited)
return len(visited) == len(rooms)
def dfs(self, rooms, cur, visited):
if cur in visited:
return
visited.append(cur)
for key in rooms[cur]:
self.dfs(rooms, key, visited)
1202. Smallest String With Swaps (Medium)
Example 1:
Input: s = “dcab”, pairs = [[0,3],[1,2]]
Output: “bacd”
Explaination:
Swap s[0] and s[3], s = “bcad”
Swap s[1] and s[2], s = “bacd”
You can swap the characters at any pair of indices in the given pairs any number of times.
Return the lexicographically smallest string that s can be changed to after using the swaps.
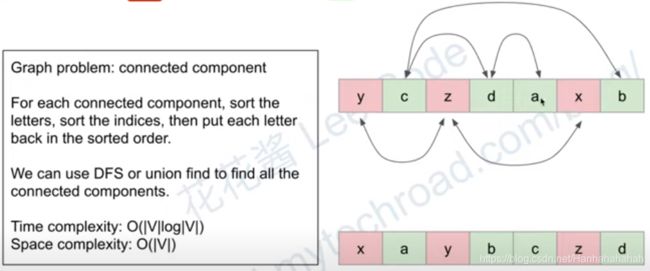
转化成图的问题。c d a b是一个连通分量, y z x是一个连通分量。连通分量内可以交换无限次数(题目中说交换任意次),所以连通分量内的字符,直接按照字母顺序lexicographically。
class Solution:
def smallestStringWithSwaps(self, s: str, pairs: List[List[int]]) -> str:
# build graph
graph = {}
for node in range(len(s)): # 初始化图
graph[node] =[]
for u,v in pairs: # 连通图
graph[u].append(v)
graph[v].append(u)
position = {} # idx -> char
for node in range(len(s)):
if node not in position:
idx = set()
self.dfs(node, idx, graph) # get connected graph idx
self.buildPos(s, idx, position) # map idx -> char by sort
res = ''
for node in range(len(s)):
res += position[node]
return res
def buildPos(self, s, idx, position):
idx_list = list(idx)
char_list = []
for idx in idx_list:
char_list.append(s[idx])
idx_list.sort()
char_list.sort()
for i in range(len(idx_list)):
position[idx_list[i]] = char_list[i]
def dfs(self, node, idx, graph):
idx.add(node)
for nei in graph[node]:
if nei not in idx:
self.dfs(nei, idx, graph)
Topology Sorting
207. Course Schedule (Medium)
There are a total of numCourses courses you have to take, labeled from 0 to numCourses-1.
Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]
Given the total number of courses and a list of prerequisite pairs, is it possible for you to finish all courses?
DFS 拓扑排序

根据列表构建出一个有向图,如果有依赖环(环内同方向),就无法全部修完。
def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
graph = [[] for _ in range(numCourses)]
visit = [0 for _ in range(numCourses)]
for x, y in prerequisites:
# graph[x]:课程x需要的prerequisite是graph[x]
graph[x].append(y)
def dfs(i): # visit: 0 has not been visited; -1 being visited; 1 has been visited
if visit[i] == -1: # 回到了自己,形成依赖环,无法完成
return False
if visit[i] == 1: # 回到已知的另一个课,可以完成
return True
visit[i] = -1 # 未知的一个课,继续检查这个未知课的prerequisite
for j in graph[i]: # 当前课的所有prerequisite
if not dfs(j):
return False
visit[i] = 1
return True
for i in range(numCourses): # 判断每一门课从它开始是否可以满足prerequisite
if not dfs(i):
return False
return True
210. Course Schedule II (Medium)
给你一些课程和它的先修课程,让你输出修课顺序。如果无法修完所有课程,返回空数组。
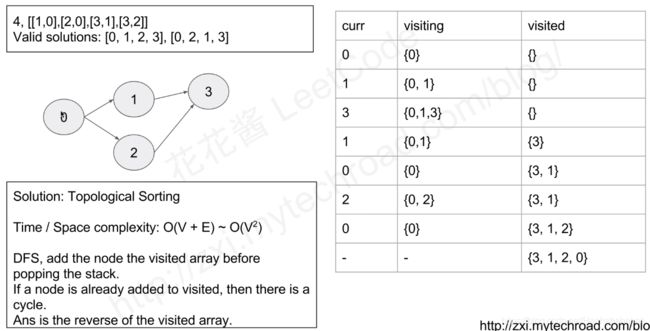
def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:
graph = [[] for _ in range(numCourses)]
visit = [0 for _ in range(numCourses)]
ans = []
for x, y in prerequisites:
# graph[x]:课程x需要的prerequisite是graph[x]
graph[x].append(y)
def dfs(i, ans): # visit: 0 has not been visited; -1 being visited; 1 has been visited
if visit[i] == -1: # 回到了自己,形成依赖环,无法完成
return False
if visit[i] == 1: # 回到已知的另一个课,可以完成
return True
visit[i] = -1 # 未知的一个课,继续检查这个未知课的prerequisite
for j in graph[i]: # 当前课的所有prerequisite
if not dfs(j, ans):
return False
visit[i] = 1
ans.append(i) ### add current course to ans
return True
for i in range(numCourses): # 判断每一门课从它开始是否可以满足prerequisite
if not dfs(i, ans):
return {}
return ans
802. Find Eventual Safe States (Medium)
Now, say our starting node is eventually safe if and only if we must eventually walk to a terminal node. Which nodes are eventually safe? Return them as an array in sorted order.
给一个有向图,找出所有不可能进入环的节点.
Example:
Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]

def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:
# unvisited -1; visiting 0; visited 1
def explore(i):
visited[i] = 0
for v in graph[i]: # 该点通向的所有点
if visited[v] == 0 or (visited[v] == -1 and explore(v)):
# 形成了环或者连接到一个环
return True # unsafe
# safe
visited[i] = 1
res.append(i)
return False
visited, res = [-1] * len(graph), []
for i in range(len(graph)):
if visited[i] == -1:
explore(i)
return sorted(res)
Union Find
399. Evaluate Division (Medium)
给出几个变量除法的结果:equations = [ [“a”, “b”], [“b”, “c”] ], values = [2.0, 3.0] (a / b =2.0, b / c = 3.0).
是否能求解queries中的除法?queries = [ [“a”, “c”], [“b”, “a”], [“a”, “e”], [“a”, “a”], [“x”, “x”] ].
Solution 1 Graph + DFS:

有向图中路径的权重全部相乘就是结果 a/b * b/c
# dfs
def calcEquation(self, equations: List[List[str]], values: List[float], queries: List[List[str]]) -> List[float]:
def divide(x, y, visited):
if x == y: return 1.0
visited.add(x)
for n in g[x]: # 遍历x的所有邻居
if n in visited: continue
visited.add(n)
d = divide(n, y, visited) # d = n/y
if d > 0: return d * g [x][n] # n/y * x/n
return -1.0
# 构建有向图
g = collections.defaultdict(dict)
for (x, y), v in zip(equations, values):
g[x][y] = v # x/y = v
g[y][x] = 1.0 / v
ans = [divide(x, y, set()) if x in g and y in g else -1 for x, y in queries]
return ans
Solution 2 Union Find:

对于任意两个节点,都在同一个tree里面(同一个根节点b),就有解:a到根节点的值 / c到根节点的值 = a/c
# Union Find
def calcEquation(self, equations: List[List[str]], values: List[float], queries: List[List[str]]) -> List[float]:
def find(x): # 找祖先
if x != U[x][0]: # 自己不是自己的祖先(有祖先)
px, pv = find(U[x][0]) # 向上一直找parent,直到没有parent(自己是自己的祖先)
U[x] = (px, U[x][1] * pv)
return U[x] # 祖先(node名,比值)
def divide(x, y): # 判断祖先是否相同
rx, vx = find(x)
ry, vy = find(y)
if rx != ry: return -1.0 # 不在一个树
return vx/vy
U = {} # U["A"] = {"B", 2.0} -> A = 2.0 * B
for (x, y), v in zip(equations, values): # 枚举,拿出 x y v (x/y=v)
if x not in U and y not in U: # 如果两个点都不在森林里:就认为y是parent
U[x] = (y, v) # x parent指向 y
U[y] = (y, 1.0) # y 指向自己
elif x not in U: # 只有一个节点在graph内
U[x] = (y, v)
elif y not in U:
U[y] = (x, 1.0/v)
else: # 两个节点都在tree里面,找他们的祖先
rx, vx = find(x)
ry, vy = find(y)
U[rx] = (ry, v / vx * vy)
ans = [divide(x, y) if x in U and y in U else -1 for x, y in queries]
return ans
721. Accounts Merge (Medium)
Example 1:
Input:
accounts = [[“John”, “[email protected]”, “[email protected]”],
[“John”, “[email protected]”],
[“John”, “[email protected]”, “[email protected]”],
[“Mary”, “[email protected]”]]
Output: [[“John”, ‘[email protected]’, ‘[email protected]’, ‘[email protected]’],
[“John”, “[email protected]”],
[“Mary”, “[email protected]”] ]
Explanation:
The first and third John’s are the same person as they have the common email “[email protected]”.
The second John and Mary are different people as none of their email addresses are used by other accounts.
We could return these lists in any order, for example the answer [[‘Mary’, ‘[email protected]’], [‘John’, ‘[email protected]’],
[‘John’, ‘[email protected]’, ‘[email protected]’, ‘[email protected]’]] would still be accepted.
Accounts[i][0] is a name, and the rest of the elements are emails representing emails of the account. 如果两个账户有相同的邮箱,那么他们是一个相同账户 合并。
*Python “|=”
s1 = {"a", "b", "c"}
s2 = {"d", "e", "f"}
s1 |= s2
{'a', 'b', 'c', 'd', 'e', 'f'}
s1 | s2
{'a', 'b', 'c', 'd', 'e', 'f'}
s1 # `s1` is unchanged
{'a', 'b', 'c'}
Solution 1 DFS:
def accountsMerge(self, accounts: List[List[str]]) -> List[List[str]]:
# DFS
d = {} # key:val = email:index
from collections import defaultdict
graph = defaultdict(list) # graph connecting the indices of the same account
for i, a in enumerate(accounts): # give each account a index number
for email in a[1:]:
if email in d:
graph[i].append(d[email])
# 把这个邮箱在已经检索过的字典中对应的账户编号加入到当前账户所在图
graph[d[email]].append(i) # 当前邮箱
else: # 还未遍历,建dict
d[email] = i
# dfs, return indices belong to the same account
def dfs(i):
tmp = {i}
for j in graph[i]:
if j not in seen:
seen.add(j)
tmp |= dfs(j)
return tmp
seen = set()
res = []
for i in range(len(accounts)):
if i in seen: # 该用户已经被加入到其他用户
continue
# set(当前账户包含的所有账户的邮箱)
res.append([accounts[i][0]] + sorted(set(email for j in dfs(i) for email in accounts[j][1:])))
return res
Solution 2 Union Find:
def accountsMerge(self, accounts: List[List[str]]) -> List[List[str]]:
# Union Find
# find root
def findroot(i):
while root[i] != i: # 没到头
root[i] = root[root[i]] # path compression
i = root[i]
return i
# union find
d = {} # key:val = email:index
root = list(range(len(accounts)))
for i, a in enumerate(accounts):
for email in a[1:]:
if email in d:
r1, r2 = findroot(i), findroot(d[email])
root[r2] = r1
else:
d[email] = i
# merge accounts
from collections import defaultdict
res0 = defaultdict(set) # key:val = index: {set of emails}
for i in range(len(accounts)):
res0[findroot(i)] |= set(accounts[i][1:])
# convert into required format
res = []
for k, v in res0.items():
res.append([accounts[k][0]] + sorted(v))
return res
737. Sentence Similarity II (Medium)
words1 = [“great”, “acting”, “skills”] and words2 = [“fine”, “drama”, “talent”] are similar, if the similar word pairs are pairs = [[“great”, “good”], [“fine”, “good”], [“acting”,“drama”], [“skills”,“talent”]]
- Similarity relation is
transitive. For example, if “great” and “good” are similar, and “fine” and “good” are similar, then “great” and “fine” are similar. - Similarity is also
symmetric. For example, “great” and “fine” being similar is the same as “fine” and “great” being similar. - Also, a word is always similar with
itself. For example, the sentences words1 = [“great”], words2 = [“great”], pairs = [] are similar, even though there are no specified similar word pairs. - Finally, sentences can only be similar if they have the
same number of words. So a sentence like words1 = [“great”] can never be similar to words2 = [“doubleplus”,“good”].
两列words如果在同一个连通分量,那么相似。如果有一个pair不在连通分量中,就不相似。检查两个顶点是否在一个连通分量。
def areSentencesSimilarTwo(self, words1, words2, pairs):
parent = {}
def find(w): # find root of each pair
if w not in parent:
parent[w] = w
while w in parent and parent[w] != w:
w = parent[w]
return w
for a, b in pairs: # 判断每一个pair是否在一个连通分量里面()
a1 = find(a)
b1 = find(b)
parent[a1] = b1
l1,l2 = len(words1),len(words2)
if l1 != l2:
return False
for i in xrange (l1):
a,b = find(words1[i]),find(words2[i])
if a != b: # 根节点不同/不在同一个连通分量
return False
return True
Bipartition & Graph coloring
785. Is Graph Bipartite? (Medium)
Given an undirected graph, return true if and only if it is bipartite. Bipartite if we can split it’s set of nodes into two independent subsets A and B such that every edge in the graph has one node in A and another node in B.
Example 1:
Input: [[1,3], [0,2], [1,3], [0,2]]
Output: true
Explanation:
The graph looks like this:
0----1
| |
| |
3----2
We can divide the vertices into two groups: {0, 2} and {1, 3}.
def isBipartite(self, graph: List[List[int]]) -> bool:
color = {}
def dfs(pos):
for i in graph[pos]: # pos的相连node
if i in color: # 已经遍历过
if color[i] == color[pos]: # 相连node竟然在同一个color
return False
else: # 没有遍历过
color[i] = 1 - color[pos] # 相连点和邻居涂不同颜色
if not dfs(i): # DFS继续沿着邻居找邻居,所有邻居都要是不同颜色
return False
return True
for i in range(len(graph)): # 遍历每一个点
if i not in color: # 该点还未上色
color[i] = 0
if not dfs(i):
return False
return True
886. Possible Bipartition (Medium)
Given a set of N people (numbered 1, 2, …, N), we would like to split everyone into two groups of any size.
Each person may dislike some other people, and they should not go into the same group.
Formally, if dislikes[i] = [a, b], it means it is not allowed to put the people numbered a and b into the same group.
Return true if and only if it is possible to split everyone into two groups in this way.
Example 1:
Input: N = 4, dislikes = [[1,2],[1,3],[2,4]]
Output: true
Explanation: group1 [1,4], group2 [2,3]
*collections.defaultdict
使用list作第一个参数,可以很容易将键-值对序列转换为列表字典。
from collections import defaultdict
s=[('yellow',1),('blue', 2), ('yellow', 3), ('blue', 4), ('red', 1)]
d=defaultdict(list)
for k, v in s:
d[k].append(v)
a=sorted(d.items())
print(a)
>>> a = [('blue', [2, 4]), ('red', [1]), ('yellow', [1, 3])]
DFS
def possibleBipartition(self, N: int, dislikes: List[List[int]]) -> bool:
# 通过不喜欢pairs构建不喜欢连通图
graph = collections.defaultdict(list)
for u, v in dislikes:
graph[u].append(v) # 记得要用append而不是“=”
graph[v].append(u)
# 下面就是判断二分图
color = {}
def dfs(node):
for i in graph[node]:
if i in color:
if color[i] == color[node]:
return False
else:
color[i] = 1 - color[node]
if not dfs(i):
return False
return True
for i in range(1, N+1):
if i not in color:
color[i] = 0
if not dfs(i):
return False
return True
1042. Flower Planting With No Adjacent (Easy)
You have N gardens, labelled 1 to N. In each garden, you want to plant one of 4 types of flowers.
paths[i] = [x, y] describes the existence of a bidirectional path from garden x to garden y.
Your task is to choose a flower type for each garden such that, for any two gardens connected by a path, they have different types of flowers.
Return any such a choice as an array answer, where answer[i] is the type of flower planted in the (i+1)-th garden. The flower types are denoted 1, 2, 3, or 4. It is guaranteed an answer exists.
def gardenNoAdj(self, N: int, paths: List[List[int]]) -> List[int]:
graph = collections.defaultdict(list)
for v, u in paths:
graph[v].append(u)
graph[u].append(v)
print(graph)
colors = [0] * N
for node in range(1, N+1):
neighbor_c = []
for nei in graph[node]: # 当前node的所有邻居
neighbor_c.append(colors[nei - 1])
for k in range(1, 5):
if k not in neighbor_c:
colors[node - 1] = k
break
return colors
In/Out Degrees
997. Find the Town Judge (Easy)
In a town, there are N people labelled from 1 to N. There is a rumor that one of these people is secretly the town judge.
If the town judge exists, then:
- The town judge trusts nobody.
- Everybody (except for the town judge) trusts the town judge.
- There is exactly one person that satisfies properties 1 and 2.
You are given trust, an array of pairs trust[i] = [a, b] representing that the person labelled a trusts the person labelled b.
If the town judge exists and can be identified, return the label of the town judge. Otherwise, return -1.
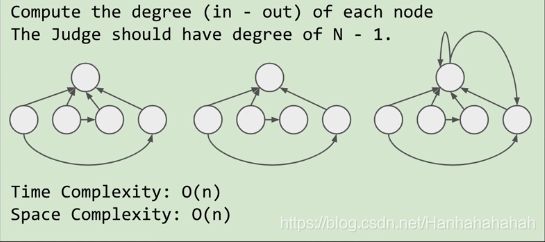
Town judge的in degree = N-1,out degree = 0 也不能相信自己。判断所有节点的degree。
def findJudge(self, N: int, trust: List[List[int]]) -> int:
degree = [0] * (N+1)
for i, j in trust:
degree[i] -= 1 # out degree + 1 -> degree - 1
degree[j] += 1 # in degree - 1 -> degree + 1
for i in range(1, N+1):
if degree[i] == N-1:
return i
return -1
Unweighted Shortest Path / BFS
433. Minimum Genetic Mutation (Medium)
A gene string can be represented by an 8-character long string, with choices from “A”, “C”, “G”, “T”. For example, “AACCGGTT” -> “AACCGGTA” is 1 mutation.
Also, there is a given gene “bank”, which records all the valid gene mutations. A gene must be in the bank to make it a valid gene string.
Now, given 3 things - start, end, bank, your task is to determine what is the minimum number of mutations needed to mutate from “start” to “end”. If there is no such a mutation, return -1.
和127 word ladder一样。
def minMutation(self, start: str, end: str, bank: List[str]) -> int:
# BFS
bankSet = set(bank)
if end not in bankSet:
print("no")
return -1
l = len(start)
s1 = {start}
s2 = {end}
bankSet.remove(end)
step = 0
while len(s1) > 0 and len(s2) > 0:
step += 1
if len(s1) > len(s2):
s1, s2 = s2, s1
s = set()
for w in s1:
print(s1)
new_words ={
w[:i] + t + w[i+1:] for t in "ACGT" for i in range(l)
}
for new_word in new_words:
if new_word in s2:
return step
if new_word not in bankSet:
continue
bankSet.remove(new_word)
s.add(new_word)
s1 = s
return -1
863. All Nodes Distance K in Binary Tree (Medium)
*We are given a binary tree (with root node root), a target node, and an integer value K.
Return a list of the values of all nodes that have a distance K from the target node. The answer can be returned in any order.
返回距离target节点距离k的节点list。
Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2
Output: [7,4,1]
Explanation:
The nodes that are a distance 2 from the target node (with value 5)
have values 7, 4, and 1.
TreeNode{val: 3, left: TreeNode{val: 5, left: TreeNode{val: 6, left: None, right: None}, right: TreeNode{val: 2, left: TreeNode{val: 7, left: None, right: None}, right: TreeNode{val: 4, left: None, right: None}}}, right: TreeNode{val: 1, left: TreeNode{val: 0, left: None, right: None}, right: TreeNode{val: 8, left: None, right: None}}}
*

- Build a undirected graph from the tree.
- Traverse the graph from target
- Collect all nodes that a re K steps from target
def buildGraph(self, node, parent, graph): # DFS to build graph
if node is None:
return
if parent is not None:
graph[node].append(parent)
if node.left is not None:
graph[node].append(node.left)
self.buildGraph(node.left, node, graph)
if node.right is not None:
graph[node].append(node.right)
self.buildGraph(node.right, node, graph)
def distanceK(self, root: TreeNode, target: TreeNode, K: int) -> List[int]:
graph = collections.defaultdict(list)
self.buildGraph(root, None, graph)
# BFS to retrieve the nodes with given distance
q = [(target, 0)] # start from the target node
visited = set()
ans = []
while q:
node, distance = q.pop()
if node in visited:
continue
visited.add(node)
# this is the desired node!!!
if K == distance:
ans.append(node.val)
# we haven't reached the desired distance, keep going
elif distance < K:
for child in graph[node]:
q.append((child, distance+1))
# when exceed the desired distance, no need to go further
return ans
1129. Shortest Path with Alternating Colors (Medium)
Consider a directed graph, with nodes labelled 0, 1, …, n-1. In this graph, each edge is either red or blue, and there could be self-edges or parallel edges.
Each [i, j] in red_edges denotes a red directed edge from node i to node j. Similarly, each [i, j] in blue_edges denotes a blue directed edge from node i to node j.
Return an array answer of length n, where each answer[X] is the length of the shortest path from node 0 to node X such that the edge colors alternate along the path (or -1 if such a path doesn’t exist).
def shortestAlternatingPaths(self, n: int, red_edges: List[List[int]], blue_edges: List[List[int]]) -> List[int]:
graph = defaultdict(lambda : defaultdict(set))
red, blue = 0, 1
for st, end in red_edges:
graph[st][red].add(end)
for st, end in blue_edges:
graph[st][blue].add(end)
print(graph)
res = [math.inf] * n
q = deque([(0,red), (0,blue)])
level = -1
while q:
level += 1
size = len(q)
for i in range(size):
node, color = q.popleft()
opp_color = color^1
res[node] = min(level, res[node])
neighbors = graph[node][opp_color]
for child in list(neighbors):
graph[node][opp_color].remove(child)
q.append((child, opp_color))
return [r if r != math.inf else -1 for r in res]
