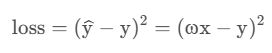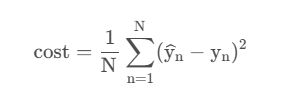【PyTorch】深度学习实践 02 线性模型

深度学习的准备过程

1. 准备数据集
2. 选择模型
3. 模型训练
4. 进行推理预测

问题

对某种产品花费 x 个工时，即可得到 y 收益，现有 x 和 y 的对应表格如下：

x （hours）	y（points）
1	2
2	4
3	6
4	8

求花费4个工时可得到的收益。

问题分析

基本流程

数据集需要交付给算法模型进行训练，利用所训练的模型，在输入新的数据时可以获得相应的输出。

我们的数据集包含了输入数据和对应的输出，所以这是监督学习（supervised learning）。

训练集和测试集

在问题给出的数据表中，前三行里的每一个 x 都有其对应的 y ，也就是每一个输入数据都有对应的输出数据，因此前三行可以作为训练集（Training Set）来对模型进行训练。

第四行只给出了 x ，其对应的输出 y 是需要我们求解的，所以把这行作为测试集（Test Set）。

验证集

测试集的标准答案一般是不会给出的，所以我们不知道训练后的模型对问题的适配度如何。

如果利用全体训练集来进行验证，那这就是一种“自己考自己”的情况，容易导致过拟合，过拟合就是模型不仅学习到针对问题的数据特征，还会额外学习到一些“噪声”，也就是训练集中的一些无关乎问题解决的特征，这就会导致接下来的测试会有更大的偏差。

为了减小这种对训练集效果好、对测试集效果较差的偏差，提升模型的泛化能力，我们将训练集分为训练集和验证集（Validation Set），此时的训练集相当于作业，而验证集相当于小测，通过小测的查缺补漏，才能让我们在接下来的考试（测试集）中获得更高的分数。

在这道题中，我们可以把数据表的前两行作为训练集，第三行作为验证集。

模型设计

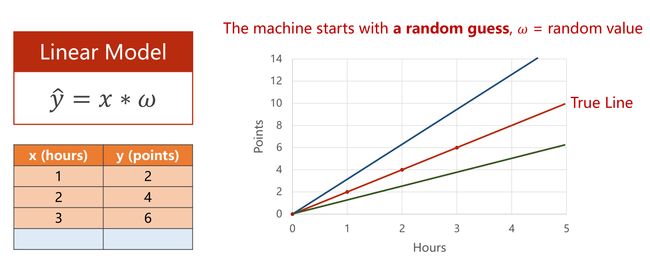
线性模型的基本模型 y = ωx + b 中，ω 和 b 是模型中的参数，训练模型的过程就是确定参数的过程。

在本问题中，将模型设置为 y = ωx，对于不同的 ω ，有不同的线性模型和图像与之对应。

模型训练过程

在模型训练中会先随机取得一个值，继而计算其和标准量之间的偏移量，从而判断当前模型是否符合预期。

记实际值为 y(x) ,模型对应的预测值为y^(x)，则其中的偏移量为∣y^(x)−y(x)∣，以此来代表模型估计值对原值的误差。

通常，该公式定义为Training Loss (Error)：

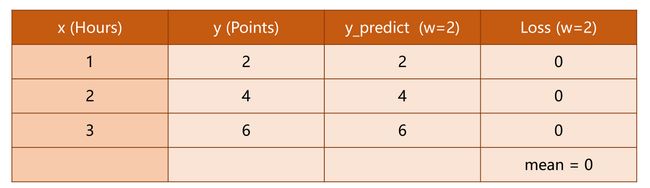
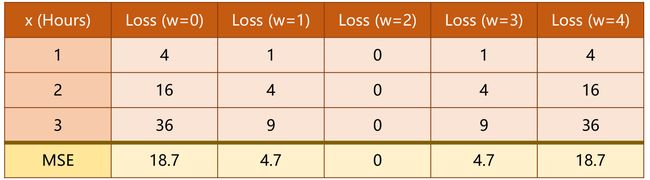
原题中的几种 ω 对应的 Loss 如下：

其中的每行为 w 不同时的单个样本的损失，最后一行为平均损失。

对于单个样本，有 Loss 可用于指代样本误差。对于所有样本，可同理用 Mean Square Error （MSE）来指代整体样本的平均平方误差（均方差cost）：

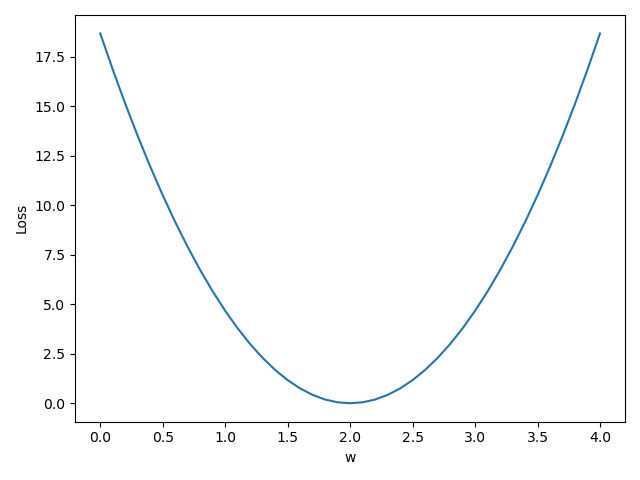
由 cost 的计算公式可知，当平均损失为0时，模型最佳，但由于仅当数据无噪声且模型完美贴合数据的情况下才会出现这种情况，因此模型训练的目的应当是尽可能小，而非找到误差为0的情况。

代码及曲线图

import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
#前馈计算
def forward(x):
    return x * w
#求loss
def loss(x, y):
    y_pred = forward(x)
    return (y_pred-y)*(y_pred-y)

w_list = []
mse_list = []
#从0.0一直到4.1以0.1为间隔进行w的取样
for w in np.arange(0.0,4.1,0.1):
    print("w=", w)
    l_sum = 0
    for x_val,y_val in zip(x_data,y_data):
        y_pred_val = forward(x_val)
        loss_val = loss(x_val,y_val)
        l_sum += loss_val
        print('\t',x_val,y_val,y_pred_val,loss_val)
    print("MSE=",l_sum/3)
    w_list.append(w)
    mse_list.append(l_sum/3)

#绘图
plt.plot(w_list,mse_list)
plt.ylabel("Loss")
plt.xlabel('w')
plt.show()