第二单元 用python学习微积分（十六）定积分
本文内容来自于学习麻省理工学院公开课：单变量微积分-定积分-网易公开课
开发环境准备：CSDN
目录
一、定积分的概念
二、计算面积的步骤
1、切割成多个"矩形"
2、把这些"矩形"的面积累加起来
3、修正前面的结果，（通过让"矩形"变窄来取得极限值，到无穷窄）
三、例子
1、 ，a = 0, b 任意
2、 f(x) = x ,a = 0, b 任意
3、f(x) = 1 ,a = 0, b 任意
四、定积分的符号（黎曼和）
1、求解定积分的通常的步骤
一、定积分的概念
几何意义找到曲线下的面积（另 累积和）
和不定积分的区别在于，不定积分并没有给出上限或下限（a,b）
二、计算面积的步骤
1、切割成多个"矩形"
2、把这些"矩形"的面积累加起来
3、修正前面的结果，（通过让"矩形"变窄来取得极限值，到无穷窄）
三、例子
1、 
，a = 0, b 任意
面积= 
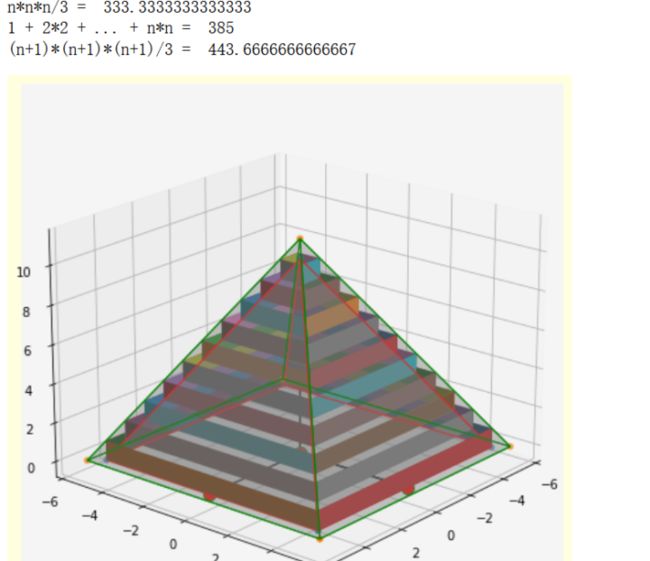
这里要计算 
， 老师给了一个算法，把数列中的每个数看作一个高为1的长方体的下底面（正方形）的一条边，这样组成了一个金字塔，另外这个金字塔有一个内接的4棱锥和一个外接的4棱锥。
体积依次为 
import matplotlib as mpl
from matplotlib import cm
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d.art3d import Poly3DCollection, Line3DCollection
from mpl_toolkits.mplot3d import Axes3D
# 创建画布
fig = plt.figure(figsize=(12, 8),
facecolor='lightyellow'
)
# 创建 3D 坐标系
ax = fig.gca(fc='whitesmoke',
projection='3d'
)
# 绘制 3D 图形
ax.plot3D(xs=[5, 0, 0, 0, 0, ], # x 轴坐标
ys=[0, 0, 5, 0, 0, ], # y 轴坐标
zs=[0, 0, 0, 0, 5, ], # z 轴坐标
zdir='z', #
c='k', # color
marker='o', # 标记点符号
mfc='r', # marker facecolor
mec='g', # marker edgecolor
ms=10, # size
)
def plot_opaque_cube(x, y, z, dx, dy, dz, ax):
xx = np.linspace(x, x+dx, 2)
yy = np.linspace(y, y+dy, 2)
zz = np.linspace(z, z+dz, 2)
xx, yy = np.meshgrid(xx, yy)
#ax.plot_surface(xx, yy, z)
#ax.plot_surface(xx, yy, z+dz)
yy, zz = np.meshgrid(yy, zz)
ax.plot_surface(x, yy, zz)
ax.plot_surface(x+dx, yy, zz)
xx, zz = np.meshgrid(xx, zz)
ax.plot_surface(xx, y, zz)
ax.plot_surface(xx, y+dy, zz)
# ax.set_xlim3d(-dx, dx*2, 20)
# ax.set_xlim3d(-dx, dx*2, 20)
# ax.set_xlim3d(-dx, dx*2, 20)
def drawPyramid(height,steps, ax, printTitle):
zFrom = 0
V = 0
for step in range(steps):
width = steps-step
plot_opaque_cube(0 - width/2, 0 - width/2, zFrom, width,width,height, ax)
V += width * width * height
zFrom += height
print(printTitle + ' = ', V)
def drawPyramid1(height,steps,ax, edgecolor, printTitle):
# vertices of a pyramid
width = steps - 0
v = np.array([[0-width/2, 0-width/2, 0], [width/2, 0-width/2, 0], [width/2, width/2, 0], [0-width/2, width/2, 0], [0, 0, height* steps]])
ax.scatter3D(v[:, 0], v[:, 1], v[:, 2])
# generate list of sides' polygons of our pyramid
verts = [ [v[0],v[1],v[4]], [v[0],v[3],v[4]],
[v[2],v[1],v[4]], [v[2],v[3],v[4]], [v[0],v[1],v[2],v[3]]]
# plot sides
ax.add_collection3d(Poly3DCollection(verts,
facecolors='gray', linewidths=1, edgecolors=edgecolor, alpha=.25))
V = width * width * height* steps / 3
print(printTitle + ' = ', V)
# 调整视角
ax.view_init(elev=20, # 仰角
azim=40 # 方位角
)
drawPyramid1(1,10, ax, 'r', 'n*n*n/3')
drawPyramid(1, 10, ax, '1 + 2*2 + ... + n*n')
drawPyramid1(1,11, ax, 'g', '(n+1)*(n+1)*(n+1)')
# 显示图形
plt.show()
接上面公式：
面积= 
(这里的重点是考虑一个无限分层的金字塔体积相当于一个4棱锥的体积，因此累加项可化简）
不等式：
所以面积：
= 
这里老师引入了求和符号
于是面积 ：
2、 f(x) = x ,a = 0, b 任意
from sympy import *
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.spines['left'].set_position('zero')
ax.spines['bottom'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set_aspect(1 )
def DrawXY(xFrom,xTo,steps,expr,color,label,plt):
yarr = []
xarr = np.linspace(xFrom ,xTo, steps)
for xval in xarr:
yval = expr.subs(x,xval)
yarr.append(yval)
y_nparr = np.array(yarr)
plt.plot(xarr, y_nparr, c=color, label=label)
def DrawRects(xFrom,xTo,steps,expr,color,plt):
width = (xTo - xFrom)/steps
xarrRect = []
yarrRect = []
area = 0
xprev = xFrom
for step in range(steps):
yval = expr.subs(x,xprev + width)
xarrRect.append(xprev)
xarrRect.append(xprev)
xarrRect.append(xprev + width)
xarrRect.append(xprev + width)
xarrRect.append(xprev)
yarrRect.append(0)
yarrRect.append(yval)
yarrRect.append(yval)
yarrRect.append(0)
yarrRect.append(0)
area += width * yval
plt.plot(xarrRect, yarrRect, c=color)
xprev= xprev + width
print('width =', width)
print('area=',area)
def TangentLine(exprY,x0Val,xVal):
diffExpr = diff(exprY)
x1,y1,xo,yo = symbols('x1 y1 xo yo')
expr = (y1-yo)/(x1-xo) - diffExpr.subs(x,x0Val)
eq = expr.subs(xo,x0Val).subs(x1,xVal).subs(yo,exprY.subs(x,x0Val))
eq1 = Eq(eq,0)
solveY = solve(eq1)
return xVal,solveY
def DrawTangentLine(exprY, x0Val,xVal1, xVal2, clr, txt):
x1,y1 = TangentLine(exprY, x0Val, xVal1)
x2,y2 = TangentLine(exprY, x0Val, xVal2)
plt.plot([x1,x2],[y1,y2], color = clr, label=txt)
def Newton(expr, x0):
ret = x0 - expr.subs(x, x0)/ expr.diff().subs(x,x0)
return ret
x = symbols('x')
expr = x
DrawXY(0,5,100,expr,'blue','',plt)
DrawRects(0,5,10,expr,'green',plt)
#plt.legend(loc='lower right')
plt.show()
可以看到每个长方形的底边为 b/n, 高为 b/n, 2b/n...
所以面积 : 
老师的计算是直接给出三角形的计算公式 width * height / 2
所以面积 : 
3、f(x) = 1 ,a = 0, b 任意
面积 : 
x = symbols('x')
expr = x**0
DrawXY(0,5,100,expr,'blue','',plt)
DrawRects(0,5,10,expr,'green',plt)
#plt.legend(loc='lower right')
plt.show()
这里老师总结了定积分的模式
猜测：
检查：
x = symbols('x')
expr = x**3
b = 1
n = 100
DrawXY(0,b,80,expr,'blue','',plt)
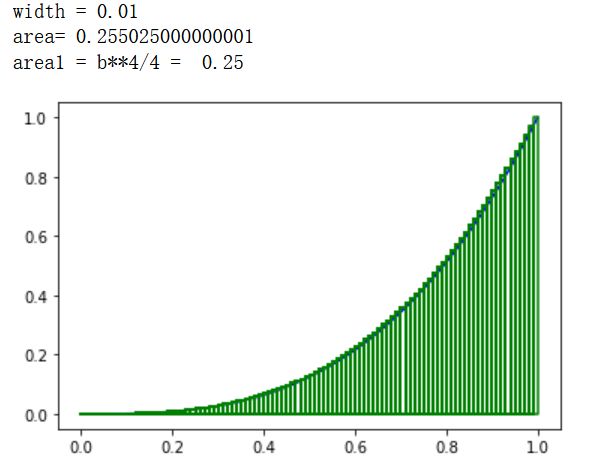
DrawRects(0,b,n,expr,'green',plt)
area1 = b / 4
print ('area1 = b**4/4 = ' , area1 )
#plt.legend(loc='lower right')
plt.show()
我们可以看到当n设为100时结果接近猜测值， 当n越大时，结果应该越接近0.25。
x = symbols('x')
expr = x**3
b = 1
n = 300
DrawXY(0,b,80,expr,'blue','',plt)
DrawRects(0,b,n,expr,'green',plt)
area1 = b / 4
print ('area1 = b**4/4 = ' , area1 )
#plt.legend(loc='lower right')
plt.show()
可以看到当n取300时，结果确实更接近0.25
四、定积分的符号（黎曼和）
1、求解定积分的通常的步骤
把所有这些间隔处的函数值累加起来就是面积（定积分的值）
(前者是黎曼和，当
趋近于0时就变成了后者的莱布尼茨的极限求值)
积分可以表达为累积和
设时间 t (yr), 有 t 的函数f(t) ($/yr)表达借钱率（每天借多少钱），假设每天都借钱，因此有 
在第45天借了钱，借了多少钱呢 ？用这个式子计算 
($)
所有如果要计算整年借到的钱,则用以下公式
（注意这个t的单位是年）
利息采用复利，那年末欠银行多少钱呢？
利率是r(可以是0.05/yr )，P（借到本金）经过时间Ｔ，欠下的钱是 
一年欠多少钱？
