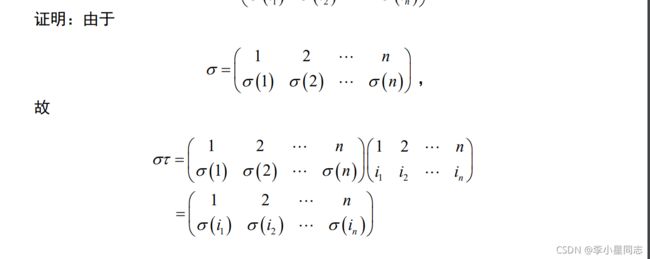近世代数:置换群、陪集指数和Lagrange定理
置换群,顾名思义,就是置换组成的群,这个置换就是双射变换的意思,因此大家都是对称群的子群。大家老换来换去的也不分谁是谁了,干脆就1234表示吧。K-循环就是大家像跑火车一样跑一圈。
无公共数码的意思是两个轮换,(注意一个轮换就是一种置换,是一种特殊的双射变换)他们没有公共的数,(这里的数要求是参加了轮换的,简单说就是这个集合有两个轮换,各自换了自己的数但对方的都原封不动地放了回去)。这时如果这两个轮换相乘的话结果肯定是井水不犯河水,各自换自己的,相乘顺序无所谓了:
先证明轮换可以表示为对换之积。就比如(1,2,3)-》(2,3,1)这是3轮换,我可以先(1,2,3)->(2,1,3)这是对换吧?在来一个(1,2,3)->(3,2,1),这也是对换吧?(2,1,3)加上这个就是(2,3,1),所以可以。那第一步怎么整呢?:
可以这样想:我要把1变成2,那2也要变成其他数,然后那个数也要其他数···数是有限的,总要到一个时候循环,那就获得了一个轮换。还有其他的元素,那就重复刚才步骤。最后就会发现一个非轮换置换都是由好几个轮换置换组成的,也就是轮换之积。
现在我可以确定每个置换都可以用对换表示了,那就有了接下来的定律:
还记得什么是排列的奇偶性吗?就是逆序数的奇偶性。逆序数就是每一个数的前面有多少比自己大的数,每个数的逆序数都加起来的结果就是排列的逆序数。一次对换将会改变一个排列的逆序数的奇偶性,而我们的m集合也可以看成一个排列(看成1234···n就可以了),现在我有一个置换,会把这个逆序数为0的序列(偶序列)变成奇序列,那我就要使用1次,3次,5次···对换,才能达到这个置换的效果,否则我就把他变成偶序列了。m(注意这个m不是上面的m集合,是记录用了几个对换的那个m)有1,3,5,7···个,那最后置换的结果就是奇的,否则就是偶的。
每个k轮换都可以写成k-1次对换的乘积.
就是一个k轮换重复k遍就会变回恒等变换的意思。不想练变换的乘积就是有两个或几个不相连轮换的置换, 那重复最小公倍数遍肯定也便会恒等变换了。
感觉用起来有点难以理解?其实就是这样:把t的原值变成6(1)···6(N),结果值变成6(i1)···6(in),也就相当是把6(1)···6(N)像123n一样对待,也就是把原来的123轮换变成了6(1)6(2)6(3)轮换。
陪集指数:
可以看到,aH一般不会是子群。当然a是e的话肯定是。
(1)H肯定包含e
(2)在子群里,乘这个群肯定出不去
(3)证明:b属于aH,假如是ac,那bH就是acH,c属于H,故cH=H,也就是bH=aH
(4)直接在左边放一个a-1
(5)直接用性质3
注1好理解,全体乘a那就没有a-1了.本身通过乘e来成为左陪集。
这证明道理很简单。每个元素都有逆元,我让逆元对应不就可以了。
竟然知道了左右陪集一样多,那我们就可以得到下面的定义:
 可以看到,我用a制造一个循环群,这个循环群是G的子群,那我们就造出了一个H,这个H的阶数肯定是G的因数吧?正好阶数又是a的阶数(我好像明白为什么他们要去一样的名字了,一个元素的阶数就是他自己循环群的阶数嘛),那不就成了。素数的话没有因数,H只能是自己了,因此是循环群。
可以看到,我用a制造一个循环群,这个循环群是G的子群,那我们就造出了一个H,这个H的阶数肯定是G的因数吧?正好阶数又是a的阶数(我好像明白为什么他们要去一样的名字了,一个元素的阶数就是他自己循环群的阶数嘛),那不就成了。素数的话没有因数,H只能是自己了,因此是循环群。
就套娃呗。
证明详解: 决定了个个像之间不会有重复的。讲道理需要的是hi-1hj不属于HnK,但这里是H的地盘,只要不在K肯定就不在HnK.同时因为不在k,这些元素也可以用于Hk,因为不满足的会重复。
决定了个个像之间不会有重复的。讲道理需要的是hi-1hj不属于HnK,但这里是H的地盘,只要不在K肯定就不在HnK.同时因为不在k,这些元素也可以用于Hk,因为不满足的会重复。
这个推论不废话?之前就可以证了。就是|G|=|H|*m的推论。但是注意了,这里要证的是“只有一个”,我只知道一定是阶数为q或者p,但现在要知道“若已经知道是q,我想知道有几个”。可以看到,如果是阶数大一点的那个的话,那就只能是一个子群。