数据结构——拓扑排序

人们当在做一件大事时，会先将大事分成许多小事分别先后去做。

比如说，我们上厕所，必须要先拿上手纸（如果你说你不用拿，那当我没说）。

当这大事足够复杂时，也就是说分成的小事足够多时，我们需要理清思路，找到一个好的方法，来决定事情的先后。

因此，拓扑排序应运而生。

首先，介绍AOV网。

AOV网（Activity On Vertex Network），AOV是一个有向无环图（Directed acyclic graph），简称DAG。

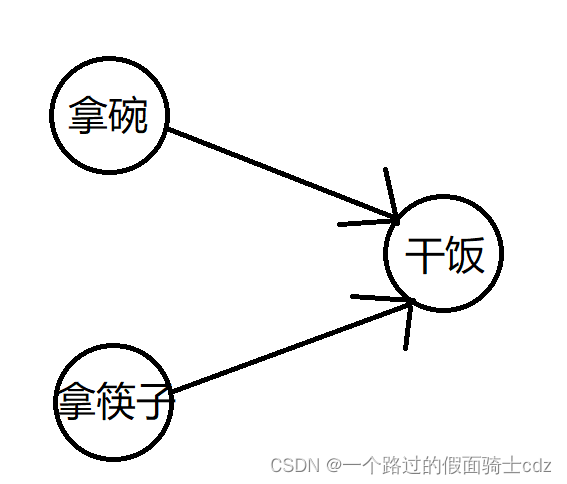
AOV网的顶点表示一个事件，比如说下面的拿碗或者拿筷子。

AOV网的有向边表示终点的事件必须先于起点。因此，也可以想到为什么用有向边。

这样的一个AOV网有助于我们分析一件大事所分成的小事的完成先后。

 有了AOV网，我们就可以借助拓扑排序算法，来给小事分个先后。

拓扑排序算法：

1.将图中入度为0的顶点输出，并将其和其出边从AOV网中删除。

2. 重复1操作，直到图中无结点或者不存在入度为0的顶点。

先展示一遍：

从上面，在（b）步骤时，我们既可以先输出c，也可以先输出f，因此得到结论：

拓扑排序不一定只有一种排序，或者说排序不唯一。

我们再来看另一种情况：

 

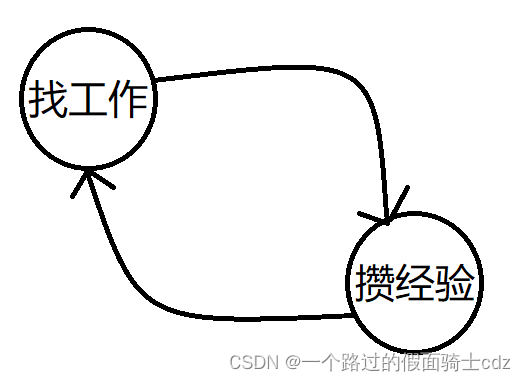
 这是一个有环图，我们发现这个环中的结点入度都不为0，因此我们不能找到其一个拓扑排序。

也就是说我们不可能完成，找工作之前要有一定的经验，而攒经验之前要找到工作，这实在是矛盾的很。

因此，拓扑排序也可以判断一个图到底是不是一个有向无环图。

判断的方法是经过拓扑排序算法之后，看是否还留有结点。

如果没有，就是DAG，否则不是。

下面是具体代码：

//test.cpp
#include
#include"Graph.h"
#include
using namespace std;
int main()
{
	cout << "请输入图中顶点数" << endl;
	int vertexNum;
	cin >> vertexNum;
    //初始化AOV图
	Graph G(vertexNum);
	//初始化入度表
	vector inDegree(vertexNum, 0);
	for (int i = 0; i < vertexNum; i++)
	{
        //每次遍历一个顶点的边表,将边表中出现的顶点的入度加一
		for (ArcNode* p = G.vertex[i].pFirst; p; p = p->next)
		{
			inDegree[p->data]++;
		}
	}
	cout << "输出入度表" << endl;
	for (int i = 0; i < inDegree.size(); i++)
		cout << inDegree[i] << " ";
	cout << endl;
	cout << "输出邻接表" << endl;
	for (int i = 0; i < vertexNum; i++)
	{
		cout << i << ":";
		for (ArcNode* p = G.vertex[i].pFirst; p; p = p->next)
		{
			cout << p->data << " ";
		}
		cout << endl;
	}
	int count = 0;//计算划去的顶点
	stack s;
    //将入度为0的压入s栈中
	for (int i = 0; i < inDegree.size(); i++)
	{
		if (!inDegree[i])
			s.push(i);
	}
	while (!s.empty())
	{
		int temp = s.top();
		s.pop();
		cout << temp << " ";//输出顶点
        count++;//划去顶点
		for (ArcNode* p = G.vertex[temp].pFirst; p; p = p->next)
		{
			inDegree[p->data]--;
            //因为划去顶点和其出边，可能会出现入度为0的边，将其压入栈中
            //且划去顶点和其出边，是入度为0的顶点产生的唯一途径
			if (!inDegree[p->data])
				s.push(p->data);
		}
	}
	cout << endl;
    //如果划去顶点数和图顶点数相等，则有拓扑排序，否则有环
	if (count == vertexNum)
		cout << "拓扑排序如上" << endl;
	else
		cout << "图中有环" << endl;
}

//VNode.h
#pragma once
#include"ArcNode.h"
class VNode//顶点定义
{
public:
	int data;//顶点
	ArcNode* pFirst;//边表
	VNode():pFirst(nullptr){}
	~VNode(){};
};

//ArcNode.h
#pragma once
class ArcNode//边表定义
{
public:
	int data;//顶点VNode指向的顶点
	ArcNode* next;//下一个顶点VNode指向的顶点
	ArcNode(int d=0):data(d),next(nullptr){}
	~ArcNode();
};

//ArcNode.cpp
#include "ArcNode.h"
ArcNode::~ArcNode()//边表结点
{
	ArcNode* p = next;
	while (p)
	{
		ArcNode* q = p;
		p = p->next;
		delete q;
	}
	next = nullptr;
}

//Graph.h
#pragma once
#include"VNode.h"
#include
#include
class Graph
{
public:
	std::vector vertex;
	Graph(int vertexNum);
	~Graph(){};
};

//Graph.cpp
#include "Graph.h"
Graph::Graph(int vertexNum)
{
	vertex = std::vector(vertexNum);
	for (int i = 0; i < vertexNum; i++)
	{
		vertex[i].data = i;//可以改为输入，这样顶点可以任意设置
		int times;
		std::cout << "顶点" << vertex[i].data << "几条出边?" << std::endl;
		std::cin >> times;
		if (times == 0)
			continue;
		std::cout << "输入边表结点" << std::endl;
		int data;
		std::cin >> data;
		vertex[i].pFirst = new ArcNode(data);
		for (int j = 0; j < times-1; j++)
		{
			std::cout << "输入边表结点" << std::endl;
			std::cin >> data;
			ArcNode* p = new ArcNode(data);
			p->next = vertex[i].pFirst->next;
			vertex[i].pFirst->next = p;
		}
	}
}