R语言结题实验报告:近年来我国城区用地变化的影响因素和驱动机制的研究
目录
- 1、小组分工
- 2、数据采集与预处理
- 2.1、数据采集与校正
- 2.2、数据异常值检验与处理
- 2.2.1缺失值检测与处理
- 2.2.2离群点检测与处理
- 3、相关性分析与相关性检验
3.1、相关性分析
3.2、相关性检验 - 4、拟合回归方程
4.1、使用主成分分析拟合一元线性回归方程
4.2、使用最小二乘法拟合多元线性回归方程 - 5、模型评估与回归诊断
- 6、结果分析
1、小组分工
A:编写代码、数据采集、整合分析过程、编写实验报告
B:数据整理、数据校正
C:数据整理、数据校正
D:查找报告有无错别字
E:对实验结果进行分析
2、数据采集与预处理
2.1、数据采集与校正
国家统计年鉴收录广泛、内容概括、信息密集、资料浓缩、编排特殊、功能齐全等特点,具有及时性、权威性与纵横比较性和多功能性,同时,统计年鉴的数据格式统一,便于使用者进行分析。数据地址为http://www.stats.gov.cn/tjsj/ndsj/2018/indexch.htm,选择的是2014-2019年统计年鉴的分地区城市建设情况。
通过观察发现除2014年数据可以直接导出为excel,其余年份数据均存放在图片中。解析每一年份网页结构,使用R语言爬虫技术批量下载每一年份的图片数据,代码如下:
library('rvest')
library('downloader')
year = c(2014:2019)
suffix = c('Z2504C','CH2504','2504CH','CH2504','CH2504','C2504')
link = c()
name = c()
# 拼接url
for (i in 1:length(year)) {
name = append(name,paste(year[i]-1,'年数据.jpg',sep = ''))
link = append(link,paste('http://www.stats.gov.cn/tjsj/ndsj/',year[i],'/html/',suffix[i],'.jpg',sep =''))
}
# 下载数据
for(i in 1:length(link)){
download(link[i],name[i], mode = "wb")
}
通过使用ocr识别技术,将下载好的图片上传到https://ocr.wdku.net/网站中,直接将图片进行识别,同时导出为excel格式文件。将文件格式化处理,同时人工进行数据校正,得到原始数据。发现每年的数据变化并不是很显著,为了方便发现自变量与因变量的关系,同时基于研究目的出发,从全国范围进行数据分析,本文将所有年份的数据进行合并,省去了数据的空间信息。
2.2、数据异常值检验与分析
2.2.1、缺失值检测
通过绘制matrixplot图,颜色越深表示数值越大,发现数据中存在两个缺失值,分别是2013年和2014年西藏的本年征用土地面积这一条数据。使用na.omit()函数将含有缺失值行进行剔除,得到进行统计分析原始数据。图表如下:
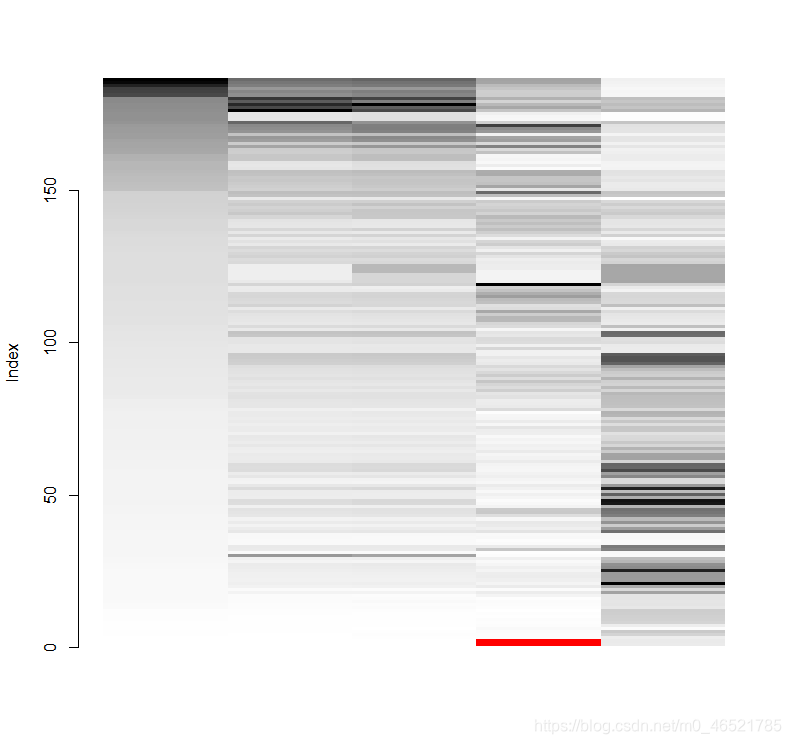
2.2.2、离群点检测
为了排除离群点对整体分析造成影响,使用水平箱形图和散点图进行异常值检测,绘制的图表如下:

通过观察发现,仅建成区面积与城市建设用地面积这两类数据存在个别离群点,其余数据聚类效果显著,因此,无需对数据使用盖帽法进行离群点剔除操作。
3、相关性分析与相关性检验
由图表可知,城市建设用地与城区面积、建成区面积、本年征用土地面积呈正相关,与城市人口密度呈负相关,提出四个假设:
- 1.城市建设用地与城区面积有关
- 2.城市建设用地与建成区面积有关
- 3.城市建设用地与本年征用土地面积有关
- 4.城市建设用地与城市人口密度有关
3.1、相关性分析
对数据进行相关性分析,由结果可知,城市建设用地与城区面积、建成区面积、本年征用土地面积呈正相关,与城市人口密度呈负相关,且城市建设用地面积与建成区面积正相关系数最大,分析结果如下:
cor(data)
城区面积 建成区面积 城市建设用地面积 本年征用土地面积 城市人口密度
城区面积 1.0000000 0.82902737 0.84112801 0.5749548 -0.42679744
建成区面积 0.8290274 1.00000000 0.96660146 0.6486980 -0.09221961
城市建设用地面积 0.8411280 0.96660146 1.00000000 0.6409767 -0.06833473
本年征用土地面积 0.5749548 0.64869803 0.64097671 1.0000000 -0.19763805
城市人口密度 -0.4267974 -0.09221961 -0.06833473 -0.1976381 1.00000000
3.2、相关性检验
为保证数据分析的科学性,需要对相关关系进行检验,进一步验证相关关系是否准确。使用psych包中的corr.test()函数可以直接得到变量之间两两相关性检验的结果,结果如下:
corr.test(data)
Probability values (Entries above the diagonal are adjusted for multiple tests.)
城区面积 建成区面积 城市建设用地面积 本年征用土地面积 城市人口密度
城区面积 0 0.00 0.00 0.00 0.00
建成区面积 0 0.00 0.00 0.00 0.43
城市建设用地面积 0 0.00 0.00 0.00 0.43
本年征用土地面积 0 0.00 0.00 0.00 0.02
城市人口密度 0 0.21 0.36 0.01 0.00
由检验结果可知,城市建设用地面积城市建设用地与城区面积有关、建成区面积有关、本年征用土地面积有关,且呈现正相关关系,与城市人口密度无关。即接受假设1、2、3,拒绝假设4。由于城市建设用地面积与城市人口密度无关,在后续分析过程中自变量由4个变为了3个,即不再分析城市建设用地面积与城市人口密度的关系。
4、拟合回归方程
4.1、使用主成分分析拟合一元线性回归方程
迭代100次,绘制数据的碎石图,可知主成分个数应为1,图表如下:

为保证数据具备自身性质,在计算过程中不对矩阵进行正交旋转操作。根据结果可知,基于非对角线值的拟合程度为0.97,可以使用主成分分析法。主成分分析结果如下:
principal(r=data1,nfactors = 1,rotate = 'none',scores = TRUE)
Principal Components Analysis
Call: principal(r = data1, nfactors = 1, rotate = "none", scores = TRUE)
Standardized loadings (pattern matrix) based upon correlation matrix
PC1 h2 u2 com
城区面积 0.91 0.82 0.18 1
建成区面积 0.94 0.88 0.12 1
本年征用土地面积 0.82 0.67 0.33 1
PC1
SS loadings 2.37
Proportion Var 0.79
Mean item complexity = 1
Test of the hypothesis that 1 component is sufficient.
The root mean square of the residuals (RMSR) is 0.12
with the empirical chi square 16.17 with prob < NA
Fit based upon off diagonal values = 0.97
通过计算主成分的得分,进行一元线性方程的拟合。使用summary函数查看结果可以得到线性方程:
![]()
4.2、使用最小二乘法拟合多元线性回归方程
使用最小二乘法拟合多元线性回归方程结果如下:
![]()
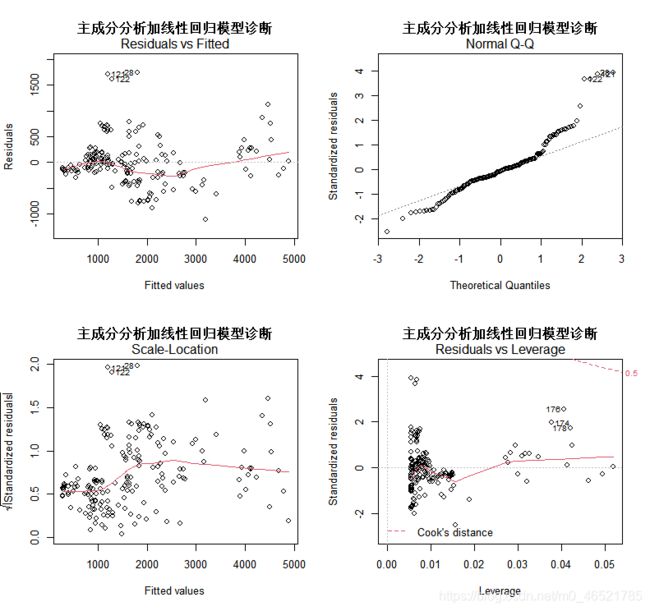
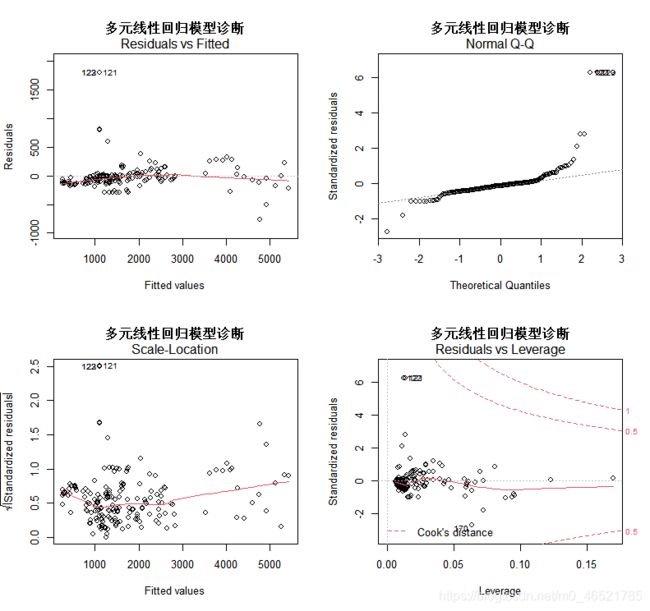
5、模型评估与回归诊断
四幅图依次代表拟合效果、QQ图、位置与尺寸图和残差与杠杆图。通过两图对比发现,两图第三幅图中点均满足随机分布,即满足不变方差的假设。除此之外,使用多元线性回归分析模型的拟合效果优于主成分分析加线性回归模型,同时其数据更加符合正态分布,离群点数较少,因此,选择多元线性回归模型作为最优回归模型。
6、结果分析
实验结果表示,城市建设用地与城区面积、建成区面积、本年征用土地面积呈正相关,与城市人口密度无关,经过我组同学搜集材料,相互交流后,对结果的分析如下: