机器学习学习笔记（3）——量纲与无量纲，标准化、归一化、正则化

量纲、无量纲，标准化、归一化、正则化是我百度了很多次都不进脑子的知识，所以我决定还是放在博客上面。
不过鉴于我查阅了很多资料，说是有许多的坑，所以我也不清楚我的理解和解释是否是坑，具体的就留给各位来帮忙评判了！

1 量纲与无量纲

1.1 量纲

量纲我觉得最重要的一句话是：物理量的大小与单位有关。

从这句话我们来思考下最核心的两个单词：大小、单位。就是说量纲是有两部分组成：数、单位。就比如1块钱和1分钱，就是两个不同的量纲，因为度量的单位不同了。

1.2 无量纲

结合上面的内容来说，那么无量纲就是：物理量大小与单位无关。

那么我们来考虑下，哪些内容是无量纲的。首先标量肯定是无量纲的，因为只有大小，没有单位。其次就是比值，因为一般来说比值都是由一个量纲除以了某个量纲后得到的，比如速度可以有“$km/s$”，“$m/s$”等等。还有一个很显眼的无量纲，就是协方差的相关系数，因为协方差的相关系数是协方差归一化后得到的结果，可以用来衡量相关性，既然能够直接拿来衡量相关性，那么就是无量纲的。

2 标准化

标准化（standardization）是一种特征缩放（feature scale）的方法，在书《python machine learning》中，关于标准化的定义如下：

Gradient descent is one of the many algorithms that benefit from feature scaling. In this section, we will use a feature scaling method called standardization, which gives our data the property of a standard normal distribution, which helps gradient descent learning to converge more quickly. Standardization shifts the mean of each feature so that it is centered at zero and each feature has a standard deviation of 1.

用我粗糙的英语翻译一下就是：

梯度下降是受益于特征缩放的算法之一。有一种特征缩放的方法叫标准化，标准化使得数据呈现正态分布，能够帮助梯度下降中学习进度收敛的更快。标准化移动特征的均值（期望），使得特征均值（期望）为0，每个特征的标准差为1。

标准化公式如下：
$$x_j^{{}^{\prime }}=\frac{x_j-{\mu }_j}{{\sigma }_j}$$

$x_j$是$n$个训练样本中第$j$个特征值组成的向量，${\mu }_j$是训练样本中的均值，${\sigma }_j$是训练样本的标准差。

关于为何标准化能够帮助到梯度下降，书本上的解释如下：

One of the reasons why standardization helps with gradient descent learning is that the optimizer has to go through fewer steps to find a good or optimal solution (the global cost minimum), as illustrated in the following figure, where the subfigures represent the cost surface as a function of two model weights in a two-dimensional classification problem:

我们先翻译解释，再解释图片：

为何标准化能够帮助梯度下降学习是因为优化器需要经历一些步骤才能找到好的或最优的方案（全局最小代价），如图所示，这表示了一个二分类问题中，关于两个权重的代价曲线函数。
而我们再来看看图，图的正中心代表着全局最优的代价（代价最小），而左边的图$w_2$方向比较宅，$w_1$方向又比较宽，那么在梯度下降的过程中，在$w_2$方向梯度会很小，所以会一直寻找最优的点，那么带来了迭代次数变多的后果，降低了效率。而当对其标准化后，变为了右图这种0均值，1标准差的情况，那么在梯度下降的过程中，不会因为某个方向梯度过小而带来更多的迭代。

3 归一化

归一化（normalization）和标准化（standardization）区别不是很大，都是特征缩放（feature scale）的方式。

有的资料中说的，归一化是把数据压缩到$[0,1]$，把量纲转为无量纲的过程，方便计算、比较等。

在书本《python machine learning》中对归一化的定义为：

Now, there are two common approaches to bring different features onto the same scale: normalization and standardization. Those terms are often used quite loosely in different fields, and the meaning has to be derived from the context. Most often, normalization refers to the rescaling of the features to a range of [0, 1], which is a special case of min-max scaling.

翻译如下：

我们有两种普通的方法来将不同的特征带到同样的范围：归一化（normalization）和标准化（standardization）。这两个术语在不同领域的使用比较松散，通常需要靠上下文来判断它们的含义。普遍情况下，归一化指的是将特征缩放到$[0,1]$这个区间，这是一个“min-max scaling”的特殊栗子。

而对于不同特征列向量来说，min-max scaling公式如下：
$$x_{norm}^{(i)}=\frac{x^i-x_{min}}{x_{max}-x_{min}}$$

其中$x^i$是这个向量中具体的某个特征，$x_{min}$是这一列特征向量中最小值，$x_{max}$是这一列特征向量中最大值。

就比如说我们有个关于西瓜的数据集，其特征为$[声音，颜色，大小]$，关于$声音$这个特征我们有三个值，构成了一个向量：$[1,5,3]$，对于这三个特征值来说，归一化后如下：
$$x_{norm}^{(1)}=\frac{1-1}{5-1}=0$$
$$x_{norm}^{(2)}=\frac{5-1}{5-1}=1$$
$$x_{norm}^{(3)}=\frac{3-1}{5-1}=0.5$$

归一化还有一点，就是说归到$[0,1]$区间后，并不会改变原本的数值大小排序关系（本想用单调性，但是感觉不妥）。就比如上面的栗子，$[1,5,3]$的大小关系为$(1,3,2)$，归一化为$[0,1,0.5]$后的大小关系依旧为$(1,3,2)$，并没有发生变化。

那么关于归一化、标准化的本质区别就是说：归一化是将特征缩放到$[0,1]$区间，标准化是把特征缩放到均值为0，标准差为1。

4 正则化

正则化（regularization）是与标准化还有归一化完全不同的东西。正则化相当于是个惩罚项，用于惩罚那些训练的太好的特征。

在书《python machine learning》中，对于正则化的描述如下：

Regularization is a very useful method to handle collinearity (high correlation among features), filter out noise from data, and eventually prevent overfitting. The concept behind regularization is to introduce additional information (bias) to penalize extreme parameter (weight) values.

我们来翻译一下：

正则化就是用来处理collinearity的，这个collinearity指的是与特征高度相关，清理掉数据的噪声，最终阻止过拟合。而正则化实际上就是引入一个额外的信息（偏置）来惩罚极端的参数（权重）值。

我们借用吴恩达老师的PPT来说：

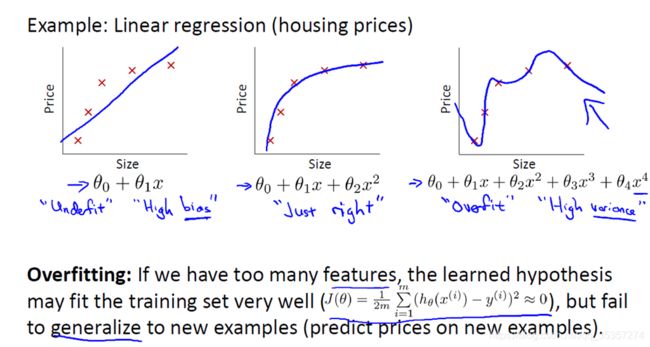
我们看到图三这个曲线非线性拟合的太完美了，那么就造成了过拟合，造成的原因是因为特征过多，训练的太好了，而这个特征过多，我个人认为就对应了上面英文中的collinearity (high correlation among features)。

我们再来分析图二和图三的公式，多了的特征是$x^3$和$x^4$，为何多了这两个就造成了图三这样的车祸现场（因为拟合的太好了，导致泛化性能很差，当有新的特征来的时候就哦豁了）？大家不妨回忆下泰勒级数，就是用多项式逼近任意一个曲线，这里也是同样的道理。那么我们要怎样解决过拟合？我们有以下两种方法：

1. 减少特征个数（特征约减）：
   1.1 手工保留部分特征（你觉得你能做到么？反正我觉得我做不到）
   1.2 模型选择算法（PCA，SVD，卡方分布）
2. 正则化：保留所有特征，惩罚系数$\theta$，使之接近于0，系数小，贡献就小。

所以也就对应了书本上的惩罚极端参数值。

正则化通常采用L2正则化，公式如下：
$$\frac{\lambda }{2}{\Vert w\Vert }^2=\frac{\lambda }{2}\sum _{j=1}^m{w}_j^2$$

其中$\lambda$称作正则化项。这里$\frac{1}{2}$是方便求导。

关于为何通常采用第二范数而非第一范数，我个人认为有如下两个理由：

1. 计算机中计算平方比计算绝对值简单；
2. 第二范数是光滑且可求导的，但是第一范数至少在0这个点是不可导的。

5 总结

1. 量纲与无量纲的区别就是：物理量是否与单位有关。
2. 标准化与归一化没有显著的区别，具体是谁要依据上下文确定。归一化是把特征缩放到$[0,1]$，标准化是把特征缩放到均值为0，标准差为1。
3. 正则化是与标准化和归一化完全不同的东西，是用于惩罚训练的太好的参数，防止模型过拟合，提高模型的泛化能力。

6 参考

[1]Sebastian Raschka,Vahid Mirjalili.Python Machine Learning[M].Packt Publishing - ebooks Account:Birmingham,2017.
[2]龚焱.标准化和归一化什么区别？[EB/OL].https://www.zhihu.com/question/20467170,2018-5-16.
[3]lcdxshengpeng.无量纲量和有量纲量[EB/OL].https://blog.csdn.net/lcdxshengpeng/article/details/82794603,2018-9-20.