网易2020校招笔试 系统开发研发工程师（提前批）牛客练习 Apare_xzc

网易2020校招笔试 系统开发研发工程师（提前批）练习

2020.9.4

---

10道选择，2道问答，4道编程
牛客链接<–

---

编程题：

1. 小易的英语软件

小易是班级的英语课代表, 他开发了一款软件开处理他的工作。
小易的软件有一个神奇的功能，能够通过一个百分数来反应你的成绩在班上的位置。“成绩超过班级 …% 的同学”。
设这个百分数为 p，考了 s 分，则可以通过以下式子计算得出 p：
p = ( 分数不超过 s 的人数 - 1) 班级总人数
突然一天的英语考试之后，软件突然罢工了，这可忙坏了小易。成绩输入这些对于字写得又快又好的小易当然没有问题，但是计算这些百分数……这庞大的数据量吓坏了他。
于是他来找到你，希望他编一个程序模拟这个软件：给出班级人数 n，以及每个人的成绩，请求出某几位同学的百分数。

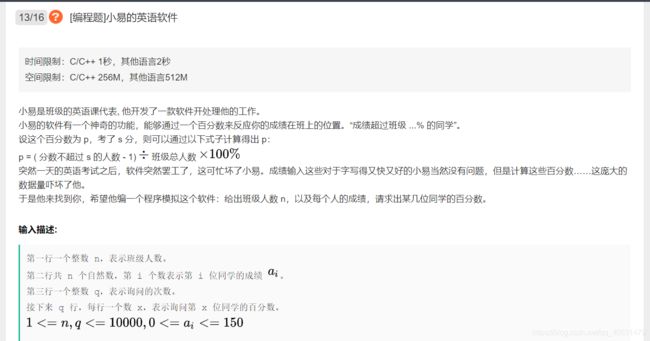
统计从0到150每个分数的总人数，然后计算前缀和，带入公式求出每个分数的p，然后输出即可。不知道为什么总说段错误，索性把数组改成了map

#include 
using namespace std;
map<int,int> a,cnt,sum;
int main(void) {
	//freopen("in.txt","r",stdin);
	int n,p,x;
	cin>>n;
	int M = 0;
	for(int i=1;i<=n;++i) {
		cin>>a[i];
		M = max(M,a[i]);
		cnt[a[i]]++;
	}
    sum[0]  = cnt[0];
	for(int i=1;i<=M;++i) 
		sum[i] = sum[i-1]+cnt[i];
	cin>>p;
	while(p--) {
		cin>>x;
		printf("%.6f\n",100.0*(sum[a[x]]-1)/n); 
	}
	return 0;
} 

---

2. 放置货物

小易有一个体积巨大的货物，具体来说，是个在二维平面上占地的货物。
小易有一个的广场，想把货物放在这个广场上。不幸的是，广场上已经有了一些障碍物，障碍物所在的格子不能放置你的货物。小易现在想知道能否成功地放置货物。


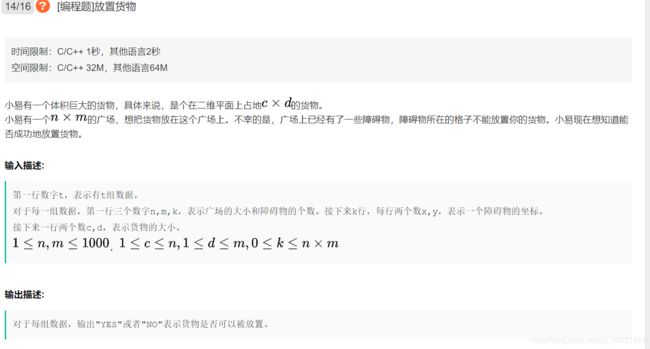
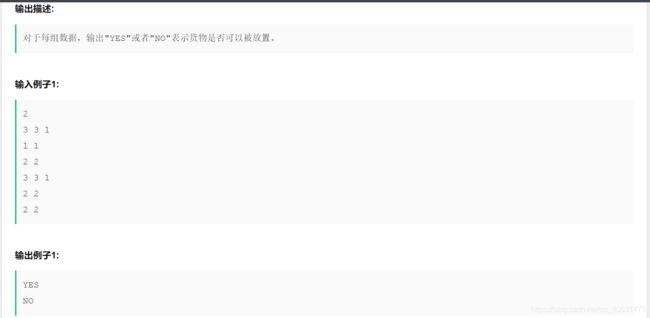
我们尝试以每个坐标为右下角，看是否可以放置。我们把有障碍的地方记为1，没有的地方记为0。维护矩阵的二维前缀和。用二维前缀和可以O(1)计算某个区域面积，只要判断是不是0即可。不是0说明有障碍物。

#include 
using namespace std;
const int N = 1000+5;
int a[N][N]; 
int sum[N][N]; 
int getSum(int x1,int x2,int y1,int y2) {
	return sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1];
}
int main(void) {
	int t,m,n,k,x,y,c,d;
	cin>>t;
	while(t--) {
		cin>>n>>m>>k;
		for(int i=1;i<=n;++i) {
			for(int j=1;j<=m;++j) a[i][j] = 0;
		}
		for(int i=1;i<=k;++i) {
			scanf("%d%d",&x,&y);
			a[x][y] = 1;
		}
		scanf("%d%d",&c,&d);
		for(int i=1;i<=n;++i) {
			for(int j=1;j<=m;++j) {
				sum[i][j] = sum[i][j-1]+a[i][j]; //横向的前缀和 
			}
		}
		for(int j=1;j<=m;++j) {
			for(int i=1;i<n;++i) sum[i+1][j]+=sum[i][j];
		} 
		for(int i=1;i<=n;++i) {
			for(int j=1;j<=m;++j) {
				if(i>=c&&j>=d&&getSum(i-c+1,i,j-d+1,j)==0) {
					puts("YES");  goto Line; 
				} else if(i>=d&&j>=c&&getSum(i-d+1,i,j-c+1,j)==0) {
					puts("YES"); goto Line;
				}
			}
		}
		puts("NO");
		Line:;
	}
	return 0;
} 

---

3. 序列维护

小易在维护数据的时候遇到一个需求，具体来说小易有一系列数据，这些数据了构成一个长度为n的数字序列，接下来小易会在这个序列上进行q次操作。
每次操作有一个查询的数字x，小易需要将序列数据中所有大于等于x的数字都减一，并输出在本次操作中有多少个数字被减一了。
小易犯了难，希望你能帮帮他。

这个题，我们发现，每次都使得>=x的数都减一，那么我们先对序列排序，每次减完仍然是有序的。
所以，如果暴力做，就每次从最大的开始减，知道当前的数 但是我们还可以每次二分查找，找出>=x的最小的数的位置P，然后把从P到n这个区间都-1。我们可以用线段树维护区间的和。因为是区间更新，所以要用lazy。二分的时候查询某一点的值其实就是一个单点查询，不过我们也可以写成更为通用的区间查询。
sum记录区间的值，lazy记录区间的懒标记。

//暴力更新
#include 
using namespace std;
const int N = 1e5+100;
int a[N];
int main(void) {
	int n,x,q;cin>>n>>q;
	for(int i=1;i<=n;++i)
		scanf("%d",a+i);
	sort(a+1,a+1+n,[](int a,int b){return a>b;
	});
	while(q--) {
		scanf("%d",&x);
		int res = 0;
		for(int i=1;i<=n;++i) {
			if(a[i]>=x) ++res,--a[i];
			else break;
		}
		printf("%d\n",res);
	}
	return 0;
} 

线段树+二分：

#include 
using namespace std;
const int N = 2e5+10;
typedef long long LL;
LL sum[N<<2],lazy[N<<2];
int a[N];
LL build(int left,int right,int pos) {
	lazy[pos] = 0;
	if(left==right) 
		return sum[pos] = a[right];
	int mid = (left+right)>>1;
	return sum[pos] = build(left,mid,pos<<1)+build(mid+1,right,pos<<1|1);
}
void push_down(int pos,int Ln,int Rn) {
	if(lazy[pos]) {
		sum[pos<<1] += lazy[pos]*Ln;
		lazy[pos<<1] += lazy[pos];
		sum[pos<<1|1] += lazy[pos]*Rn;
		lazy[pos<<1|1] += lazy[pos];
		lazy[pos] = 0;
	}
}
LL query(int left,int right,int qL,int qR,int pos) {
	if(left>qR||right<qL) return 0;
	if(qL<=left&&right<=qR) return sum[pos];
	int mid = (left+right)>>1;
	push_down(pos,mid-left+1,right-mid);
	return query(left,mid,qL,qR,pos<<1)+query(mid+1,right,qL,qR,pos<<1|1);
}
LL update(int left,int right,int uL,int uR,int add,int pos) {
	if(left>uR||right<uL) return sum[pos];
	if(uL<=left&&right<=uR) {
		lazy[pos] += add;
		return sum[pos] = sum[pos]+(right-left+1)*add;
	}
	int mid = (left+right)>>1;
	push_down(pos,mid-left+1,right-mid);
	return sum[pos] = update(left,mid,uL,uR,add,pos<<1)+update(mid+1,right,uL,uR,add,pos<<1|1);
}
int main(void) {
//	freopen("in2.txt","r",stdin);
	int n,Q,x;
	scanf("%d%d",&n,&Q);
	for(int i=1;i<=n;++i)
		scanf("%d",a+i);
	sort(a+1,a+1+n);
	build(1,n,1); 
	while(Q--) {
		scanf("%d",&x);
		if(query(1,n,n,n,1)<x) {
			puts("0");continue;
		}
		int L = 0, R = n; //(]
		while(R-L>1) {
			int mid = (L+R)>>1;
			if(query(1,n,mid,mid,1)>=x) R = mid;
			else L = mid;
		}
		printf("%d\n",n-R+1);
		update(1,n,R,n,-1,1);
	}
	return 0;
} 

---

4. 按位或

小易有一个初始为空的数字集合，支持两种操作：
1、加入数字x到集合中。
2、询问集合中是否存在一个子集，满足子集中所有数字的Or值恰好为k。
Or为二进制按位或操作，C++中表示为"|"。
小易希望你能解决这个问题。


根据或或运算的性质，如果要选出子集使得相或的和为x, 那么就不能在x为0的位置上有1。我们把所有的满足这个条件的元素或起来，只要能凑出x的所有1的位，就是YES。 如果y没有比x多出1的位，那么y|x==x。 我们只需要把列表中和x或的结果等于x的所有数都或起来，如果能凑出x，就是YES，如果半中间凑出了x，就可以提前break了。

#include 
using namespace std;
const int N = 1e5+100;
bool vis[N]; 
int main(void) {
	vector<int> v;
	int q,op,x;
	cin>>q;
	while(q--) {
		scanf("%d%d",&op,&x);
		if(op==1) {
			if(!vis[x]) v.push_back(x),vis[x]=true;
		} else {
			int y = 0;
			for(auto t:v) {
				if((t|x)==x) {
					y|=t;
					if(y==x) {
						puts("YES");goto Line;
					}
				}
			}
			puts("NO"); 
			Line:;
		}	
	}
	return 0;
} 

又是N²过1E5…

---

问答题

1. java数据库开发中怎么理解两个方法数据库操作在一个事务里面，事务和数据库连接池有什么关系，JTA事务和普通事务的区别

vicyor
1.数据库的事务交给JDBC的Connection去处理.
connection.autoCommit(false); //相当于在数据库端开启事务 start transaction;
connection.setTransactioIsolation(isolation); //设置隔离级别;
connection.commit(); //提交事务
connection.rollback(savePoint);//回滚
2.JTA是指Java Transaction API,JTA允许应用程序执行分布式事务处理.
分布式事务(distributed transaction)包括一个事务管理器(transaction manager)和一个或多个资源管理器(resource manager).
发表于 2020-02-17 17:54:57

2. 在并发编程有个名称叫线程安全，怎么理解一个类是线程安全

vicyor
1.安全性是指不会有意外的事情发生.
2.一个类是线程安全的指的是该类的域不会因为并发修改而出现一致性问题.
发表于 2020-02-17 17:55:40

越努力越幸运k
这个类我们称之为资源类，使用多个线程去操作资源类；
一般的操作是具有顺序性的，单线程时候就是方法顺序执行，方法对数据操作后再把数据写回去，下一个方法在对数据进行操作，所以不会出现读一些错误的数据，或者被修改后的数据没有及时的写回到内存中；
如果一个类是线程安全的，那么相当于在这个类的对象和和模板上加了一把锁一样，当一个线程在操作这个类的时候，其他的线程是不被允许同时操作的，只有等这个线程完成对资源类的操作后，其他的线程才可以获得这个锁，操作资源类，继续加锁，执行，解锁。
常见的保持一个类线程安全的方法有：
1、使用 sychronized 线程同步锁
2、使用 Lock 对需要操作的 对象加锁
等等
发表于 2020-04-06 22:48:22

慕宗悫之长风
类的线程安全：一个类能表现出正确的行为，称这个类是线程安全的。
如何保证线程安全：
（1）栈封闭。
（2）将状态变量修改为不可变变量。
（3）对于必须要共享的变量：
1、独占锁的方式：synchronized
2、volatile修饰变量：只能保证可见性不能保证一致性，适合用于当前要修改的值不依赖于先前值的情况。
3、显示锁。Lock接口的各种实现。
4、原子变量。

---

选择题

interface Alpha {
    void f();
}
class Beta implements Alpha {
    public void f() {
        System.out.println("Beta.f()");
    }
    public void g() {
        System.out.println("Beta.g()");
    }
}
public class Main {
    public static void main(String[] args) {
        Alpha a = new Beta();
        a.f();
        System.out.println(a.getClass().getName());
        try {
            Beta b = (Beta)a;
            b.g();
        } catch (Exception e) {
            System.out.println("Error");
        }
    }
}

掌心里的小雨
考点：Java–多态
口诀：
1.调用成员变量：编译和运行都参考左边。
2.调用成员方法（非静态）：编译看左边，运行看右边
3.调用静态方法：编译和运行都看左边。
题目中第14行代码Alpha a = new Beta();是多态的实现
题目中第15行代码a.f();是调用成员成员方法，满足口诀第2条，编译看左边，运行看右边，编译阶段看左边，Alpha接口中含有f()方法，所以编译通过，运行时看右边，所以调用的是Beta类中的f()方法，所以输出Beta.f();
题目中第16行代码a.getClass().getName()中的a.getClass()同理运行调用的是Beta类的Object父类的本地方法public final native Class getClass();，得到Beta类的Class对象，最后再调用Class类中的public String getName()方法，最后输出Beta;
题目中第18行代码Beta b = (Beta)a;向下转型为Beta类对象，所以可以直接调用Beta类的g()方法，最后输出Beta.g()。
发表于 2020-08-04 16:13:21

vicyor
1.NIO是同步非阻塞,通过选择器Selector监听多个通道(Channel),响应其感兴趣的事件(每个通道在选择器上注册的事件).(Reactor模式)
发表于 2020-02-17 16:30:14

tigg_ZZ
可以细分出几种情况：
1）i += 1; 这种情况下在 i = 0 之上赋值 0+1也就是输出 1
2）i = i++； 第一步：i++这个表达式会返回 0，但此时 i = 1； 第二步：将返回值 0 赋值给 i ；第三步： i 又被更改为 0，所以输出 0
3）i = ++i; 第一步： ++i这个表达式会返回1，同时 i = 1； 第二步：将返回值 1 赋值给 i ； 第三步：i = 1
4）i++； 很常用的方式，这里的返回值并没有赋值给任何变量，所以在输出时，会发现 i = 1；
编辑于 2020-07-29 22:49:02

我是复读机
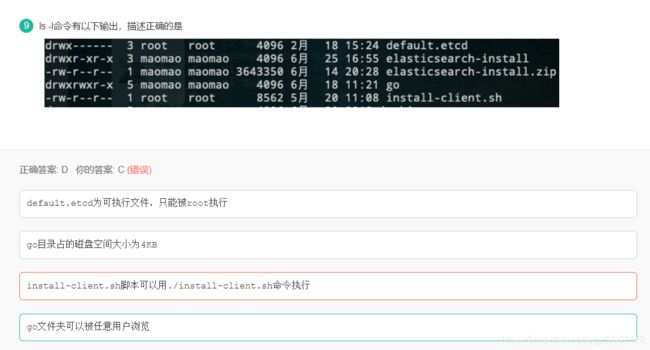
A是目录，不是文件；
B也是目录，所以4096表示的是该目录符所占的大小（注意，4096不表示该目录下所有文件的大小）；
C没有x权限，不能直接./运行，但可以用sh运行；
D正确
发表于 2020-04-21 19:41:36

vicyor
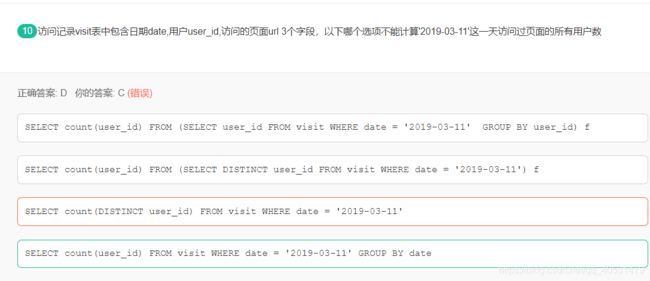
D . SELECT count(user_id) FROM visit WHERE date = ‘2019-03-11’ GROUP BY date
问题: 1.user_id未去重
2.已经通过where 选出date了,group by 无意义.
修改: SELECT count(user_id) FROM visit WHERE date = ‘2019-03-11’ GROUP BY user_id
发表于 2020-02-17 16:47:43

---

2020.9.4
19:45

---