LeetCode 209. 长度最小的子数组

长度最小的子数组

题目链接 209. 长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度**。**如果不存在符合条件的子数组，返回 0 。

示例 1：

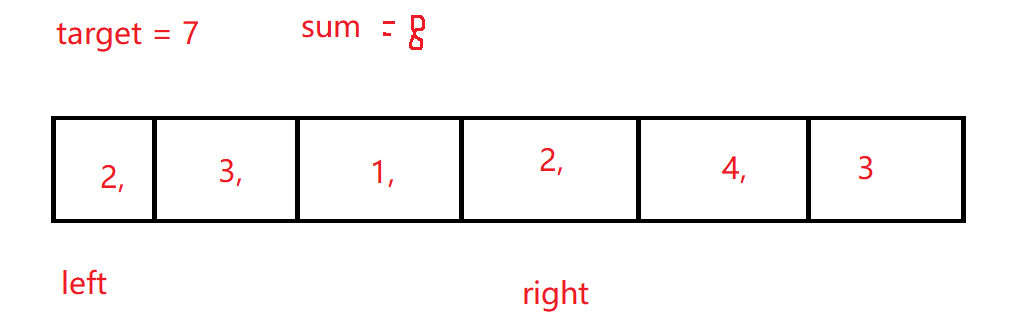
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

题目解释

这道题目是在众多子数组中,找到我们改子数组的总和大于等于target的情况,并且我们希望子数组的元素个数最少.

算法原理

下面我们说一下我们的暴力的想法,我们可以使用两层循环,判断我们的子数组的元素和.

for(i=0; i < num.size(); i++)
{
    int sum = num[i];
    for(j = i+1; j < num.size(); j++)
    {
        if(sum == target)
        {
            // 记录我们的子数组的长度
        }
          
        sum += num[j];
    }
}

如果我们仔细看题目,那么我们会发现我们数组的元素都是正整数,这就造成了我们的如果累加元素,那么和一定是增加的,这里可以做一个优化.

for(i=0; i < num.size(); i++)
{
    int sum = num[i];
    for(j = i+1; j < num.size(); j++)
    {
        if(sum == target)
        {
            // 记录我们的子数组的长度
            break; // 没有必要继续下去了
        }
        else if(sum > target)
        {
            break; // 没有必要继续下去了
        }
        sum += num[j];
    }
}

这里我们还是发现的,我们并没有本质的优化.下面说我们的方法二,这里我们按照示例 1来举例子.这里我们可以很容易发现我们使用的是双指针, 那么为何我们使用双指针可以解决这个问题?还是因为我们的额和具有单调性,你会发现在我们寻找一个子数组中我们的和总是增加的,

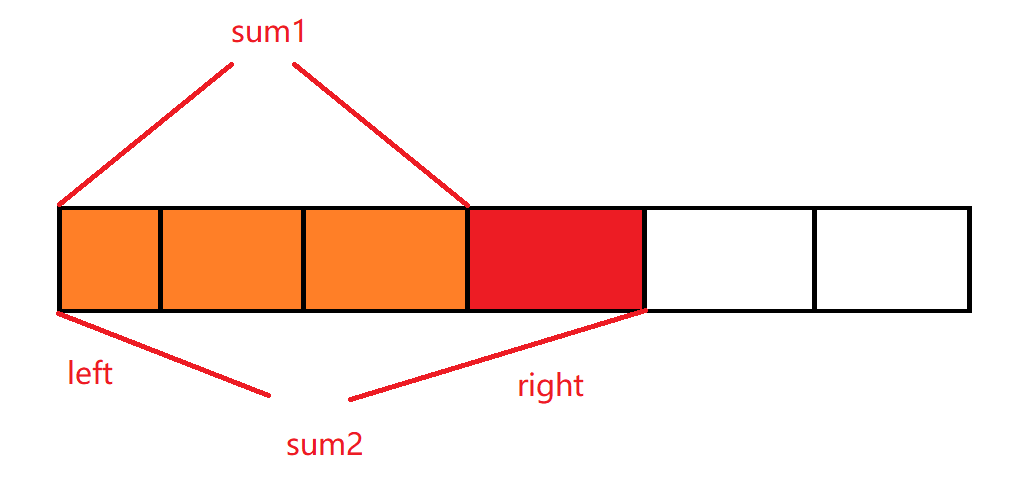
当我们的sum大于等于我们的target,你会发现我们以下标left=0的子数组所有情况已经结束了,下面就是我们的让left向后移动,这里请问我们right需要重新初始化和left一样吗?需要的,但是我们这里不是必须的,下面解释下

• 原本的sum == target,那么我们left右移后新的sum一定小于target,如果我们初始化right,他还是会走的这个位置的
• 原本的sum > target,这个我们需要讨论下

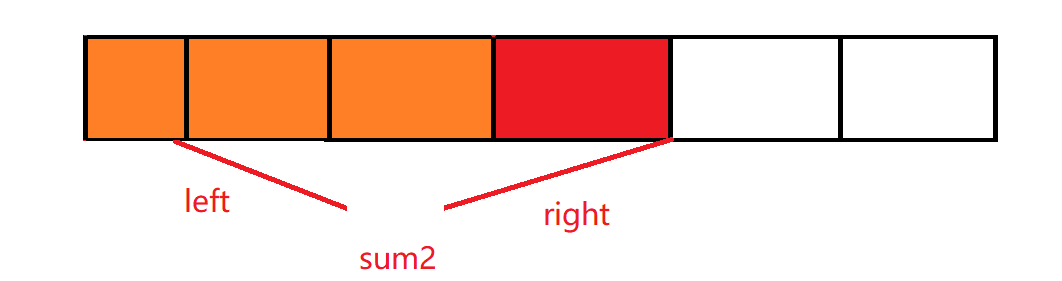
一旦出现第二种情况,也就是sum2>target,但是这里隐含一个事情,那么就是我们的sum1

• sum2 < target,这里非常好,我们可以继续向后遍历right
• sum2 > target,这里只能证明一点,以新的left作为起点的子数组是没有复合条件的,要知道我们所有的sum1都是小于target,但是加入一个元素就大于了,后面怎么可能

前面我们说了很多,但是可以总结为两点

• 使用双指针, 可以使用双指针是因为这里的sum是单调的
• left和right只会通向,始终沿着一个方向移动

像这种模式,我们有另外一个名词,就是滑动窗口.是的,他的本质还是我们的双指针.只不过我们的left和right是窗口的两个边.滑动窗口的步骤一般是下面这样的

• 定义left和right变量
• 进窗口
• 判断结果
• 出窗口

这里还有一个更新结果的步骤,不过具体的问题具体分析.关于我谈的这些步骤,希望大家是理解他,可以作为一个参考的大纲,但不是一定符合的.

细节补充

上面我们都是大篇幅的谈了滑动窗口,通过这道题目补充些细节,看代码

int ret = INT_MAX;   // 这是结果
int left = 0, right = 0;
int sum = 0; // 子数组的和
while(right < n)
{
    sum += num[right];  // 进窗口
    while(sum >= target)// 这就是判断,为何是while,可能出现这样的情况  num = [1 1 1 1 1000] target = 10000 
    {
        ret = min(ret,right-left+1); // 更新结果
        sum -= num[left++];  // 出窗口
    }
    right++;
}

代码编写

class Solution
{
public:
  int minSubArrayLen(int target, vector &nums)
  {
    int ret = INT_MAX; // 这是结果
    int left = 0, right = 0;
    int sum = 0; // 子数组的和
    int n = nums.size();
    while (right < n)
    {
      sum += nums[right];    // 进窗口
      while (sum >= target) // 这就是判断,为何是while,可能出现这样的情况  num = [1 1 1 1 1000] target = 10000
      {
        ret = min(ret, right - left + 1); // 更新结果
        sum -= nums[left++];               // 出窗口
      }
      right++;
    }
    return ret == INT_MAX ? 0 : ret;
  }
};