opencv 单目相机pnp测距(Cpp)
概述
单目相机pnp测距是通过单目相机拍摄的一张2d图片,来测量图片中某物与相机的距离。
需要知道被测物的实际尺寸
测距前需要先相机标定,需要使用哪个相机进行测距就标定哪个。一旦换成了其他相机, 就要重新标定最终相机。
为什么要相机标定?
相机标定是为了得到从 3d世界中任意一点映射到相机拍摄得的 图片上对应点的 坐标变换细节。
上述坐标变换可以用矩阵运算式描述。
相机标定是为了获得 相机内参矩阵 。
相机内参矩阵只与相机本身有关,所以更换相机就需要获得新相机的两个矩阵,而与更换被测目标物体无关。
相机成像相关原理
相机内参矩阵:包括相机矩阵和畸变系数。
相机矩阵:[fx, 0, cx; 0, fy, cy; 0,0,1]。其中焦距(fx, fy),光学中心(cx, cy)。
畸变系数:畸变数学模型的5个参数k1,k2, P1, P2, k3。
相机外参:通过旋转和平移变换将点在3d世界的坐标转换为2d图像的平面坐标,其中的旋转矩阵和平移矩阵被称为相机外参。
相机成像的坐标变换过程:
3d世界坐标系-->相机坐标系:【3d世界的物体相对于世界原点的3维坐标】转换为【该物体以相机镜头中心为坐标原点时的3维坐标】
相机坐标系-->图像坐标系:【该物体以相机镜头中心为坐标原点时的3维坐标】转换为【成像到图像传感器上的2维坐标】
图像坐标系-->像素坐标系:图像坐标系上为连续的信息,对其采样,转换为非连续的像素
相机标定
准备
本文采用张正友标定法,标定板使用棋盘格。(标定的目的是获取相机内参,用什么方法、什么标定板不重要)
棋盘格可以使用opencv安装目录下自带的图片。(pip下载的python版不知道有没有)
D:\opencv\sources\samples\data (参考此路径)注:将图片打印到纸上,可以缩放,但图片比例不要变。
标定时需要查找棋盘格的角点。
实测若棋盘格上覆盖有反光材料的时候极可能会 找不到角点(即便用肉眼看相机拍出来的图片根本看不出反光)。包括 用屏幕显示棋盘格、 在棋盘格纸上贴透明胶带。
拍摄标定要用的图片
运行一下代码
#include
#include
#include
using namespace cv;
using namespace std;
int main()
{
VideoCapture inputVideo(0);
if (!inputVideo.isOpened())
{
cout << "Could not open the input video " << endl;
return -1;
}
Mat frame;
Mat frameCopy;
string imgname;
vector image_points_buf;
bool isFound;
int f = 1;
while (1)
{
inputVideo >> frame;
frame.copyTo(frameCopy);
if (frame.empty())
break;
// 在未找到角点时,视频会很卡。可以将30到33行注释掉
isFound = findChessboardCorners(frameCopy, Size(7, 7), image_points_buf);
if(isFound)
drawChessboardCorners(frameCopy, Size(7, 7), image_points_buf, isFound);
imshow("Camera", frameCopy);
char key = waitKey(1);
if (key == 'q' || key == 'Q') // quit退出
break;
if (key == 'k' || key == 'K') // 拍摄当前帧
{
cout << "frame:" << f << endl;
imgname = "snapPhotos/"+to_string(f++) + ".jpg";
imwrite(imgname, frame);
}
}
cout << "Finished writing" << endl;
return 0;
} 上述代码会把拍摄的图片保存到当前工作目录下的snapPhotos文件夹内。
注:若代码无误,运行过程也没报错,运行完却找不到所拍摄的图片,可以看我这篇文章:https://blog.csdn.net/qq_35858902/article/details/128933950
在当前工作目录下新建calibdata.txt文件,填入一下内容(不要有空格,最后不要空行,别忘记保存):
snapPhotos/1.jpg
snapPhotos/2.jpg
snapPhotos/3.jpg
snapPhotos/4.jpg
snapPhotos/5.jpg
snapPhotos/6.jpg
snapPhotos/7.jpg
snapPhotos/8.jpg
snapPhotos/9.jpg
snapPhotos/10.jpg若上面拍摄图片时,你没有保存到snapPhotos文件夹内,则需修改为你保存的实际路径。上为相对路径,也可以使用绝对路径:
D:/project_root/snapPhotos/1.jpg开始标定
运行以下代码
此代码自https://blog.csdn.net/u012319493/article/details/77622053稍有修改
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace cv;
using namespace std;
void main()
{
ifstream fin("calibdata.txt"); /* 标定所用图像文件的路径 */
ofstream fout("caliberation_result.txt"); /* 保存标定结果的文件 */
// 读取每一幅图像,从中提取出角点,然后对角点进行亚像素精确化
int image_count = 0; /* 图像数量 */
Size image_size; /* 图像的尺寸 */
Size board_size = Size(7, 7); /* 标定板上每行、列的角点数 */
vector image_points_buf; /* 缓存每幅图像上检测到的角点 */
vector> image_points_seq; /* 保存检测到的所有角点 */
string filename; // 图片名
vector filenames;
while (getline(fin, filename))
{
++image_count;
Mat imageInput = imread(filename);
filenames.push_back(filename);
//imshow("file", imageInput);
//waitKey(0);
// 读入第一张图片时获取图片大小
if (image_count == 1)
{
image_size.width = imageInput.cols;
image_size.height = imageInput.rows;
}
/* 提取角点 */
if (findChessboardCorners(imageInput, board_size, image_points_buf) == false)
{
cout << "can not find chessboard corners!找不到角点\n"; // 找不到角点
exit(1);
}
else
{
Mat view_gray;
cvtColor(imageInput, view_gray, COLOR_BGR2GRAY); // 转灰度图
/* 亚像素精确化 */
// image_points_buf 初始的角点坐标向量,同时作为亚像素坐标位置的输出
// Size(5,5) 搜索窗口大小
// (-1,-1)表示没有死区
// TermCriteria 角点的迭代过程的终止条件, 可以为迭代次数和角点精度两者的组合
cornerSubPix(view_gray, image_points_buf, Size(5, 5), Size(-1, -1), TermCriteria(TermCriteria::EPS + TermCriteria::MAX_ITER, 30, 0.1));
image_points_seq.push_back(image_points_buf); // 保存亚像素角点
/* 在图像上显示角点位置 */
drawChessboardCorners(view_gray, board_size, image_points_buf, false); // 用于在图片中标记角点
imshow("Camera Calibration", view_gray); // 显示图片
waitKey(500); //暂停0.5S
}
}
int CornerNum = board_size.width * board_size.height; // 每张图片上总的角点数
//-------------以下是摄像机标定------------------
/*棋盘三维信息*/
Size square_size = Size(2.6, 2.6); /* 实际测量得到的标定板上每个棋盘格的两边长,单位自定,但要保持统一 */
vector> object_points; /* 保存标定板上角点的三维坐标 */
/*内外参数*/
Mat cameraMatrix = Mat(3, 3, CV_32FC1, Scalar::all(0)); /* 摄像机内参数矩阵 */
vector point_counts; // 每幅图像中角点的数量
Mat distCoeffs = Mat(1, 5, CV_32FC1, Scalar::all(0)); /* 摄像机的5个畸变系数:k1,k2,p1,p2,k3 */
vector tvecsMat; /* 每幅图像的旋转向量 */
vector rvecsMat; /* 每幅图像的平移向量 */
/* 初始化标定板上角点的三维坐标 */
int i, j, t;
for (t = 0; t < image_count; t++)
{
vector tempPointSet;
for (i = 0; i < board_size.height; i++)
{
for (j = 0; j < board_size.width; j++)
{
Point3f realPoint;
/* 假设标定板放在世界坐标系中z=0的平面上 */
realPoint.x = i * square_size.width;
realPoint.y = j * square_size.height;
realPoint.z = 0;
tempPointSet.push_back(realPoint);
}
}
object_points.push_back(tempPointSet);
}
/* 初始化每幅图像中的角点数量,假定每幅图像中都可以看到完整的标定板 */
for (i = 0; i < image_count; i++)
{
point_counts.push_back(board_size.width * board_size.height);
}
/* 开始标定 */
// object_points 世界坐标系中的角点的三维坐标
// image_points_seq 每一个内角点对应的图像坐标点
// image_size 图像的像素尺寸大小
// cameraMatrix 输出,内参矩阵
// distCoeffs 输出,畸变系数
// rvecsMat 输出,旋转向量
// tvecsMat 输出,位移向量
// 0 标定时所采用的算法
calibrateCamera(object_points, image_points_seq, image_size, cameraMatrix, distCoeffs, rvecsMat, tvecsMat, 0);
//------------------------标定完成------------------------------------
// -------------------对标定结果进行评价------------------------------
double total_err = 0.0; /* 所有图像的平均误差的总和 */
double err = 0.0; /* 每幅图像的平均误差 */
vector image_points2; /* 保存重新计算得到的投影点 */
fout << "每幅图像的标定误差:\n";
for (i = 0; i < image_count; i++)
{
vector tempPointSet = object_points[i];
/* 通过得到的摄像机内外参数,对空间的三维点进行重新投影计算,得到新的投影点 */
projectPoints(tempPointSet, rvecsMat[i], tvecsMat[i], cameraMatrix, distCoeffs, image_points2);
/* 计算新的投影点和旧的投影点之间的误差*/
vector tempImagePoint = image_points_seq[i];
Mat tempImagePointMat = Mat(1, tempImagePoint.size(), CV_32FC2);
Mat image_points2Mat = Mat(1, image_points2.size(), CV_32FC2);
for (int j = 0; j < tempImagePoint.size(); j++)
{
image_points2Mat.at(0, j) = Vec2f(image_points2[j].x, image_points2[j].y);
tempImagePointMat.at(0, j) = Vec2f(tempImagePoint[j].x, tempImagePoint[j].y);
}
err = norm(image_points2Mat, tempImagePointMat, NORM_L2);
total_err += err /= point_counts[i];
fout << "第" << i + 1 << "幅图像的平均误差:" << err << "像素" << endl;
}
fout << "总体平均误差:" << total_err / image_count << "像素" << endl << endl;
//-------------------------评价完成---------------------------------------------
//-----------------------保存定标结果-------------------------------------------
Mat rotation_matrix = Mat(3, 3, CV_32FC1, Scalar::all(0)); /* 保存每幅图像的旋转矩阵 */
fout << "相机内参数矩阵:" << endl;
fout << cameraMatrix << endl << endl;
fout << "畸变系数:\n";
fout << distCoeffs << endl << endl << endl;
for (int i = 0; i < image_count; i++)
{
fout << "第" << i + 1 << "幅图像的旋转向量:" << endl;
fout << tvecsMat[i] << endl;
/* 将旋转向量转换为相对应的旋转矩阵 */
Rodrigues(tvecsMat[i], rotation_matrix);
fout << "第" << i + 1 << "幅图像的旋转矩阵:" << endl;
fout << rotation_matrix << endl;
fout << "第" << i + 1 << "幅图像的平移向量:" << endl;
fout << rvecsMat[i] << endl << endl;
}
fout << endl;
//--------------------标定结果保存结束-------------------------------
//----------------------显示定标结果--------------------------------
Mat mapx = Mat(image_size, CV_32FC1);
Mat mapy = Mat(image_size, CV_32FC1);
Mat R = Mat::eye(3, 3, CV_32F);
string imageFileName;
std::stringstream StrStm;
for (int i = 0; i != image_count; i++)
{
initUndistortRectifyMap(cameraMatrix, distCoeffs, R, cameraMatrix, image_size, CV_32FC1, mapx, mapy);
Mat imageSource = imread(filenames[i]);
Mat newimage = imageSource.clone();
remap(imageSource, newimage, mapx, mapy, INTER_LINEAR);
StrStm.clear();
imageFileName.clear();
StrStm << i + 1;
StrStm >> imageFileName;
imageFileName += "_d.jpg";
imageFileName = "calibrated/" + imageFileName;
imwrite(imageFileName, newimage);
}
fin.close();
fout.close();
return;
} -上述代码第23行board_size,(7, 7)指棋盘格内部横纵各有7个角点,如果你用的是本文提供的opencv自带的棋盘格,则不需要修改。
- 第76行看注释自行修改
运行成功后会在当前工作目录下生成一个caliberation_result.txt文件,里面有内参矩阵。
测距
运行如下代码:
#include
#include
using namespace std;
using namespace cv;
int main(int argc, char** argv)
{
Mat image = imread("test.jpg");
//被测物某个平面需要特征点,特征点可以是角点,但需要可测出实际坐标
//2d图像特征点像素坐标,可以用鼠标事件找出特征点坐标
vector image_points;
image_points.push_back(Point2d(298, 159));
image_points.push_back(Point2d(380, 159));
image_points.push_back(Point2d(380, 240));
image_points.push_back(Point2d(298, 240));
// 画出特征点
for (int i = 0; i < image_points.size(); i++)
{
circle(image, image_points[i], 3, Scalar(0, 0, 255), -1);
}
// 3D 特征点世界坐标,与像素坐标对应,单位是与标定时填的实际测量棋盘格大小的单位相同,如同是cm或同是mm
//世界坐标指所选的特征点在物理世界中的3d坐标,坐标原点自己选。
//下面以物块平面正中心为坐标原点,x正方向朝右,y正方向朝下
std::vector model_points;
model_points.push_back(Point3d(-1.4f, -1.45f, 0)); // 左上角(-1.4cm,-1.45cm)
model_points.push_back(Point3d(+1.4f, -1.45f, 0));
model_points.push_back(Point3d(+1.4f, +1.45f, 0));
model_points.push_back(Point3d(-1.4f, +1.45f, 0));
// 注意世界坐标和像素坐标要一一对应
// 相机内参矩阵和畸变系数均由相机标定结果得出
// 相机内参矩阵
Mat camera_matrix = (Mat_(3, 3) << 659.9293277147924, 0, 145.8791713723572,
0, 635.3941888799933, 120.2096985290085,
0, 0, 1);
// 相机畸变系数
Mat dist_coeffs = (Mat_(5, 1) << -0.5885200737681696, 0.6747491058456546, 0.006768694852797847,
0.02067272313155804, -0.3616453058722507);
cout << "Camera Matrix " << endl << camera_matrix << endl << endl;
// 旋转向量
Mat rotation_vector;
// 平移向量
Mat translation_vector;
// pnp求解
solvePnP(model_points, image_points, camera_matrix, dist_coeffs, \
rotation_vector, translation_vector, 0, SOLVEPNP_ITERATIVE);
// ITERATIVE方法,其他方法参照官方文档
cout << "Rotation Vector " << endl << rotation_vector << endl << endl;
cout << "Translation Vector" << endl << translation_vector << endl << endl;
Mat Rvec;
Mat_ Tvec;
rotation_vector.convertTo(Rvec, CV_32F); // 旋转向量转换格式
translation_vector.convertTo(Tvec, CV_32F); // 平移向量转换格式
Mat_ rotMat(3, 3);
Rodrigues(Rvec, rotMat);
// 旋转向量转成旋转矩阵
cout << "rotMat" << endl << rotMat << endl << endl;
Mat P_oc;
P_oc = -rotMat.inv() * Tvec;
// 求解相机的世界坐标,得出p_oc的第三个元素即相机到物体的距离即深度信息,单位是mm
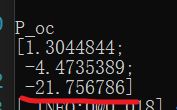
cout << "P_oc" << endl << P_oc << endl;
imshow("Output", image);
waitKey(0);
} 第12、27、36、40行,看注释修改。
运行成功后终端会输出信息,P_oc最后一个数即为距离,单位跟之前一致。
本文使用的单位是cm,故测出来约为21.7568cm