python栈的实现与应用
文章目录
- 什么是栈?
- 用Python实现栈
- 栈的应用:简单括号匹配
- 栈的应用:十进制转换为二进制
- 栈的应用:表达式转换
什么是栈?
栈有时也被称作“下推栈”。它是一种有次序的数据项集合,添加操作和移除操作总发生在同一端,即“顶端”,另一端则被称为“底端”。
栈中的元素离底端越近,代表其在栈中的时间越长,因此栈的底端具有非常重要的意义。最新添加的元素将被最先移除。这种排序原则被称作LIFO ( last-in first-out ),即后进先出。这是一种基于数据项保存时间的次序,时间越短的离栈顶越近,而时间越长的离栈底越近。最近添加的元素靠近顶端,旧元素则靠近底端。
日常生活中有很多栈的应用,如盘子、托盘、书堆等等。
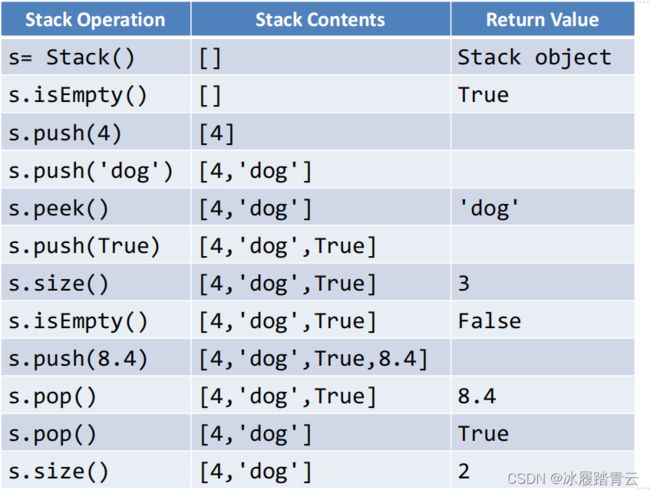
我们观察一个由混合的python原生数据对象形成的栈:
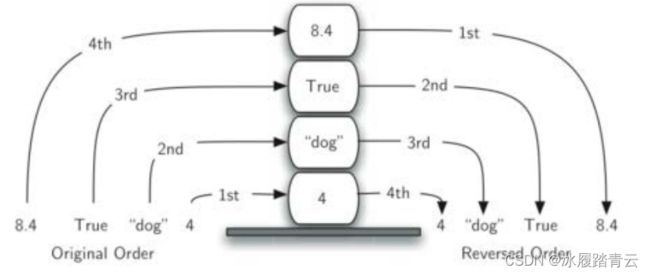
进栈和出栈的次序正好相反。
这种访问次序反转的特性,我们也在某些计算机操作上碰到过。
比如浏览器的“后退back”按钮,当我们从一个网页跳转到另一个网页时,这些网页——实际上是 URL—都被存放在一个栈中。当前正在浏览的网页位于栈的顶端,最早浏览的网页则位于底端。如果点击返回按钮,便开始反向浏览这些网页。
抽象数据类型“栈”定义为如下的操作:
Stack():创建一个空栈,不包含任何数据项
push(item):将item加入栈顶,无返回值
pop():将栈顶数据项移除,并返回,栈被修改
peek():“窥视”栈顶数据项,返回栈顶的数据项但不移除,栈不被修改
isEmpty():返回栈是否为空栈
size():返回栈中有多少个数据项
用Python实现栈
在清楚地定义了抽象数据类型Stack之后,我们看看如何用Python来实现它。
Python的面向对象机制可以用来实现用户自定义类型,将ADT Stack实现为Python的一个Class,将ADT Stack的操作实现为Class的方法,由于Stack是一个数据集,所以可以采用Python的原生数据集来实现,我们选用最常用的数据集List来实现。
Python列表是有序集合,它提供了一整套方法。举例来说,对于列表[2,5,3,6,7,4] ,只需要考虑将它的哪一边视为栈的顶端。一旦确定了顶端,所有的操作就可以利用 append 和pop等列表方法来实现。
可以将List的任意一端(index=0或者-1)设置为栈顶,我们这里选用List的末端(index=-1)作为栈顶,这样栈的操作就可以通过对list的append和pop来实现:
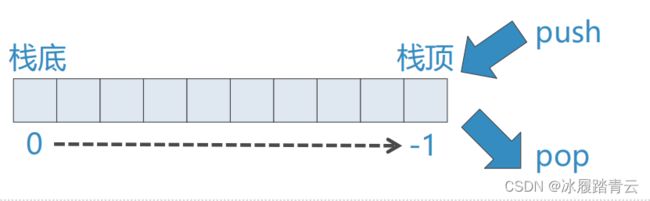
需要注意的是如果我们把List的另一端(首端index=0 )作为Stack的栈顶,同样也可以实现Stack:
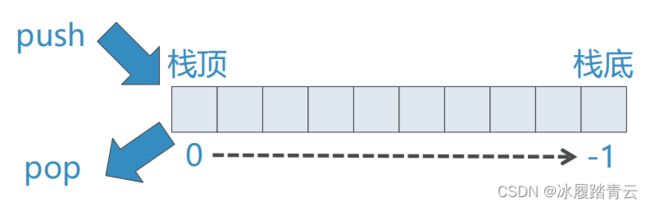

改变抽象数据类型的实现却保留其逻辑特征,这种能力体现了抽象思想。不过,尽管上述两种实现都可行,但是二者在性能方面肯定有差异。append方法和 pop( )方法的时间复杂度都是o(1),这意味着不论栈中有多少个元素,栈顶尾端的实现(右)中的push操作和 pop操作都会在恒定的时间内完成。栈顶首端的版本(左)实现的性能则受制于栈中的元素个数,这是因为insert (0)和 pop(0)的时间复杂度都是O(n),元素越多就越慢。显而易见,尽管两种实现在逻辑上是相等的,但是它们在进行基准测试时耗费的时间会有很大的差异。
栈的应用:简单括号匹配
我们都写过这样的表达式:
( 5 + 6 ) ∗ ( 7 + 8 ) / ( 4 + 3 ) (5+6)∗(7+8)/(4+3) (5+6)∗(7+8)/(4+3)
这里的括号是用来指定表达式项的计算优先级,匹配括号是指每一个左括号都有与之对应的一个右括号,并且括号对有正确的嵌套关系。
对括号是否正确匹配的识别,是很多语言编译器的基础算法。
下面看看如何构造括号匹配识别算法:
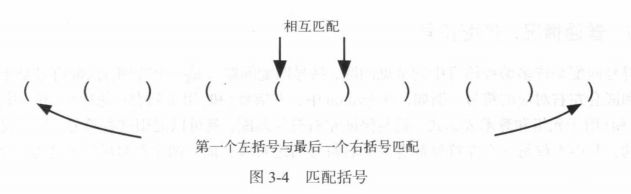
从左到右扫描括号串,最新打开的左括号,应该匹配最先遇到的右括号,这样,第一个左括号(最早打开),就应该匹配最后一个右括号(最后遇到)这种次序反转的识别,正好符合栈的特性!
一旦认识到用栈来保存括号是合理的,算法编写起来就会十分容易。由一个空栈开始,从左往右依次处理括号。如果遇到左括号,便通过push操作将其加入栈中,以此表示稍后需要有一个与之匹配的右括号。反之,如果遇到右括号,就调用pop操作。只要栈中的所有左括号都能遇到与之匹配的右括号,那么整个括号串就是匹配的;如果栈中有任何一个左括号找不到与之匹配的右括号,则括号串就是不匹配的。在处理完匹配的括号串之后,栈应该是空的。代码清单3-3展示了实现这一算法的 Python代码。

parChecker函数假设stack类可用,并且会返回一个布尔值来表示括号串是否匹配。注意,布尔型变量balanced 的初始值是True,这是因为一开始没有任何理由假设其为False,如果当前的符号是左括号,它就会被压入栈中(第9-10行)。注意第15行,仅通过pop()将一个元素从栈中移除。由于移除的元素一定是之前遇到的左括号,因此并没有用到pop()的返回值。在第19~22行,只要所有括号匹配并且栈为空,函数就会返回True,否则返回False。
在实际的应用里,我们会碰到更多种括号,如python中列表所用的方括号“[]”
字典所用的花括号“{}”,元组和表达式所用的圆括号“()” ,这些不同的括号有可能混合在一起使用, 因此就要注意各自的开闭匹配情况。

栈的应用:十进制转换为二进制
二进制是计算机原理中最基本的概念,作为组成计算机最基本部件的逻辑门电路,其输入和输出均仅为两种状态:0和1 。
但十进制是人类传统文化中最基本的数值概念,如果没有进制之间的转换,人们跟计算机的交互会相当的困难。
所谓的“进制”,就是用多少个字符来表示整数。
十进制是0~9这十个数字字符,二进制是0、1两个字符。
我们经常需要将整数在二进制和十进制之
间转换
如: ( 233 ) 10 (233)_{10} (233)10的对应二进制数为 ( 11101001 ) 2 (11101001)_2 (11101001)2,
具体是这样:
( 233 ) 10 = 2 × 1 0 2 + 3 × 1 0 1 + 3 × 1 0 0 (233)_{10}=2×10^2+3×10^1+3×10^0 (233)10=2×102+3×101+3×100
( 11101001 ) 2 = 1 × 2 7 + 1 × 2 6 + 1 × 2 5 + 0 × 2 4 + 1 × 2 3 + 0 × 2 2 + 0 × 2 1 + 1 × 2 0 (11101001)_2=1×2^7+1×2^6+1×2^5+0×2^4+1×2^3 +0×2^2+0×2^1+1×2^0 (11101001)2=1×27+1×26+1×25+0×24+1×23+0×22+0×21+1×20
十进制转换为二进制,采用的是除以2求余数的算法,将整数不断除以2,每次得到的余数就是由低到高的二进制位。
“除以2”算法假设待处理的整数大于0。它用一个简单的循环不停地将十进制数除以2,并且记录余数。第一次除以2的结果能够用于区分偶数和奇数。如果是偶数,则余数为0,因此个位上的数字为0;如果是奇数,则余数为1,因此个位上的数字为1。可以将要构建的二进制数看成一系列数字;计算出的第一个余数是最后一位。如图3-5所示,这又一次体现了反转特性,因此用栈来解决该问题是合理的。

十进制转换为二进制代码实现:

十进制转换为二进制的算法,很容易可以扩展为转换到任意N进制,只需要将除以2求余数算法改为“除以N求余数”算法就可以。
二进制有两个不同数字0、1
十进制有十个不同数字0、1、2、3、4、5、6、 7、8、9
八进制可用八个不同数字0、1、2、3、4、5、6 、7
十六进制的十六个不同数字则是0、1、2、3、4 、5、6、7、8、9、A、B、C、D、E、F
十进制转换为十六以下任意进制代码示例:
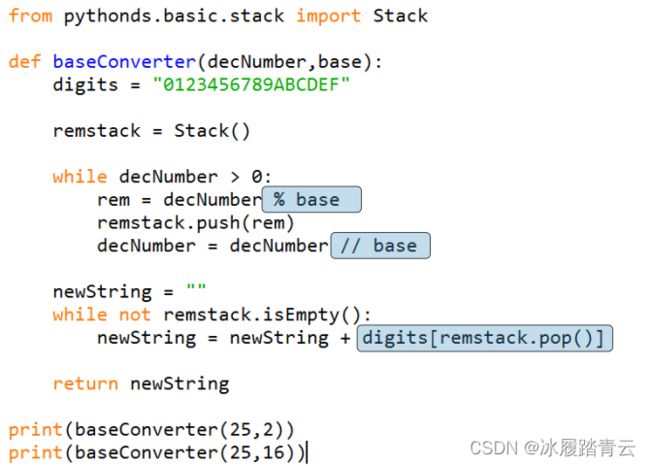
为了实现这一方法,第3行创建了一个数字字符串来存储对应位置上的数字。0在位置0,1在位置1,A在位置10,B在位置11,依此类推。当从栈中移除一个余数时,它可以被用作访问数字的下标,对应的数字会被添加到结果中。如果从栈中移除的余数是13,那么字母D将被添加到结果字符串的最后。
栈的应用:表达式转换
我们通常看到的表达式像这样: B ∗ C B*C B∗C,很容易知道这是B乘以C ,这种操作符介于操作数中间的表示法,称为中缀表示法。但有时候中缀表示法会引起混淆,如 “A+B*C” 是A+B然后再乘以C,还是 B ∗ C B*C B∗C然后再去加A?
人们引入了操作符优先级的概念来消除混淆,规定高优先级的操作符先计算
相同优先级的操作符从左到右依次计算,这样 A + B ∗ C A+B*C A+B∗C就没有疑义是A加上B与C的乘积,同时引入了括号来表示强制优先级,括号的优先级最高,而且在嵌套的括号中,内层的优先级更高,这样(A+B)*C就是A与B的和再乘以C。
虽然人们已经习惯了这种表示法,但计算机处理最好是能明确规定所有的计算顺序,这样无需处理复杂的优先规则。
引入全括号表达式:在所有的表达式项两边都加上括号,
A + B ∗ C + D A+B*C+D A+B∗C+D,应表示为 ( ( A + ( B ∗ C ) ) + D ) ((A+(B*C))+D) ((A+(B∗C))+D)
可否将表达式中操作符的位置稍移动一下?例如中缀表达式A+B,将操作符移到前面,变为“+AB”,或者将操作符移到最后,变为“AB+” 。
我们就得到了表达式的另外两种表示法:
“前缀”和“后缀”表示法,以操作符相对于操作数的位置来定义。
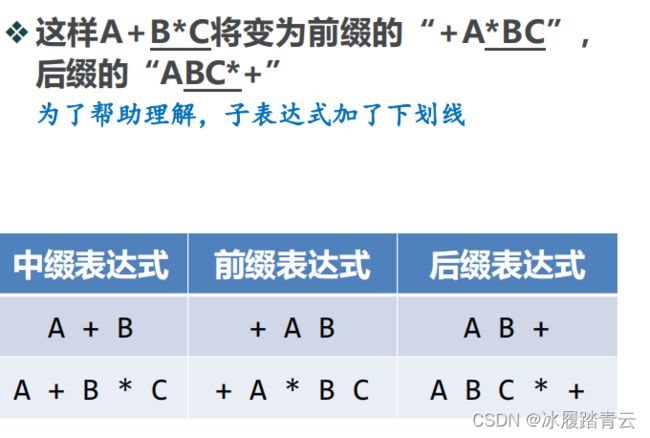

神奇的事情发生了,在中缀表达式里必须的括号,在前缀和后缀表达式中消失了? 在前缀和后缀表达式中,操作符的次序完全决定了运算的次序,不再有混淆,所以在很多情况下,表达式的计算机表示都避免用复杂的中缀形式。
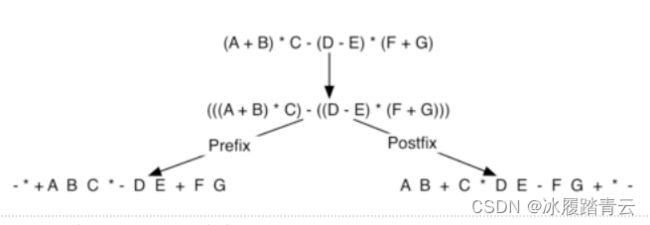
下面看更多的例子:
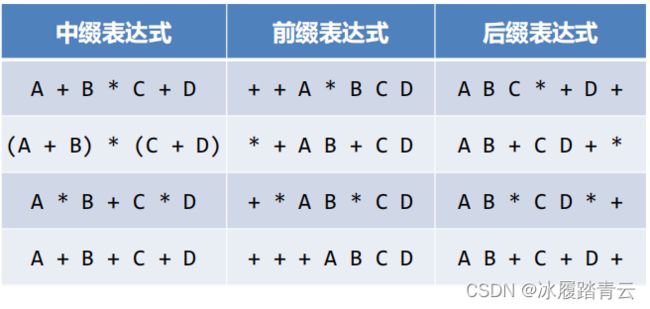
目前为止我们仅手工转换了几个中缀表达式到前缀和后缀的形式,一定得有个算法来转换任意复杂的表达式。
为了分解算法的复杂度,我们从“全括号”中缀表达式入手,
我们看A+B*C,如果写成全括号形式:
( A + ( B ∗ C ) ) (A+(B*C)) (A+(B∗C)),显式表达了计算次序
我们注意到每一对括号,都包含了一组完整的操作符和操作数。
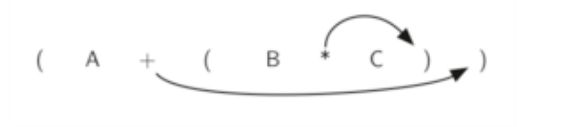
看子表达式 ( B ∗ C ) (B*C) (B∗C)的右括号,如果把操作符 ∗ * ∗移到右括号的位置,替代它,再删去左括号,得到 B C ∗ BC* BC∗,这个正好把子表达式转换为后缀形式,进一步再把更多的操作符移动到相应的右括号处替代之,再删去左括号,那么整个表达式就完成了到后缀表达式的转换。
同样的,如果我们把操作符移动到左括号的位置替代之,然后删掉所有的右括号,也就得到了前缀表达式:
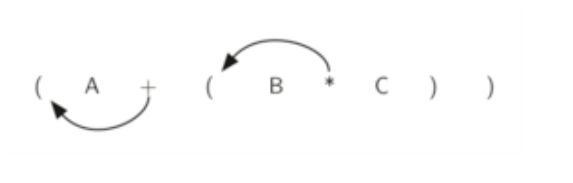
所以说,无论表达式多复杂,需要转换成前缀或者后缀,只需要两个步骤:
我们来讨论下通用的中缀转后缀算法,首先我们来看中缀表达式 A + B ∗ C A+B*C A+B∗C,其对应的后缀表达式是 A B C ∗ + ABC*+ ABC∗+,操作数ABC的顺序没有改变。
操作符的出现顺序,在后缀表达式中反转了,由于*的优先级比+高,所以后缀表达式中操作符的出现顺序与运算次序一致。
在中缀表达式转换为后缀形式的处理过程中,操作符比操作数要晚输出,所以在扫描到对应的第二个操作数之前,需要把操作符先保存起来,而这些暂存的操作符,由于优先级的规则,还有可能要反转次序输出。 在 A + B ∗ C A+B*C A+B∗C中,+虽然先出现,但优先级比后面这个 ∗ * ∗要低,所以它要等*处理完后,才能再处理。
这种反转特性,使得我们考虑用栈来保存暂时未处理的操作符。
再看看 ( A + B ) ∗ C (A+B)*C (A+B)∗C,对应的后缀形式是 A B + C ∗ AB+C* AB+C∗
这里+的输出比 ∗ * ∗要早,主要是因为括号使得+的优先级提升,高于括号之外的 ∗ * ∗ ,后缀表达式中操作符应该出现在左括号对应的右括
号位置,所以遇到左括号,要标记下,其后出现的操作符。优先级提升了,一旦扫描到对应的右括号,就可以马上输出这个操作符。
总结下,在从左到右扫描逐个字符扫描中缀表达式的过程中,采用一个栈来暂存未处理的操作符,这样,栈顶的操作符就是最近暂存进去的,当遇到一个新的操作符,就需要跟栈顶的操作符比较下优先级,再行处理。
中缀表达式单词列表扫描结束后,把opstack栈中的所有剩余操作符依次弹出
,添加到输出列表末尾,把输出列表再用join方法合并成后缀表达式字符串,算法结束。
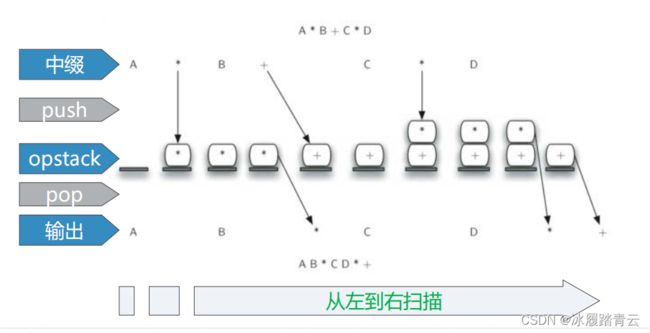
Python实现从中序表达式到后序表达式的转换:

以上成功实现了从中序表达式到后序表达式,下面我们试着计算后缀表达式,跟中缀转换为后缀问题不同, 在对后缀表达式从左到右扫描的过程中, 由于操作符在操作数的后面, 所以要暂存操作数,在碰到操作符的时候
,再将暂存的两个操作数进行实际的计算。仍然是栈的特性:操作符只作用于离它最近的两个操作数。
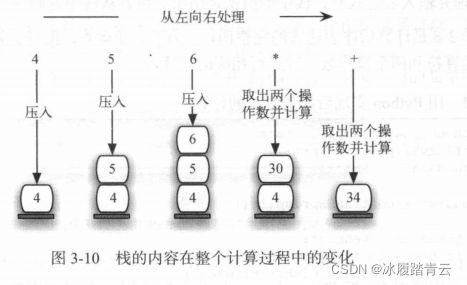
如“4 5 6 * +”,我们先扫描到4、5两个操作数,但还不知道对这两个操作数能做什么计算,需要继续扫描后面的符号才能知道,继续扫描,又碰到操作数6 ,还是不能知道如何计算,继续暂存入栈直到*,现在知道是栈顶两个操作数5 、6做乘法。我们弹出两个操作数,计算得到结果30。
需要注意:
先弹出的是右操作数,后弹出的是左操作数,这个对于-/很重要!
为了继续后续的计算,需要把这个中间结果30压入栈顶,继续扫描后面的符号,当所有操作符都处理完毕,栈中只留下1个操作数,就是表达式的值。
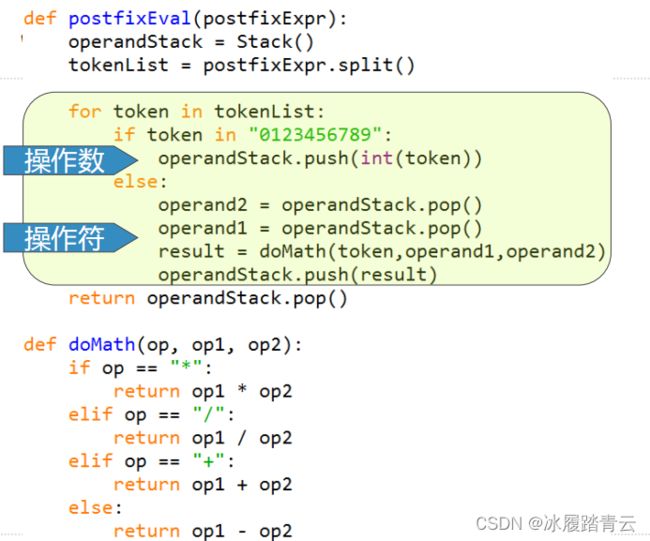
后缀表达式求值流程:
(1) 创建空栈operandstack。
(2) 使用字符串方法 split将输入的后序表达式转换成一个列表。
(3) 从左往右扫描这个标记列表。如果标记是操作数,将其转换成整数并且压入operandstack栈中。如果标记是运算符,从operandstack栈中取出两个操作数。第一次取出右操作数,第二次取出左操作数。进行相应的算术运算,然后将运算结果压入 operandstack栈中。
(4) 当处理完输入表达式时,栈中的值就是结果。将其从栈中返回。