2.1 向量与线性方程组
一、行图像与列图像
线性代数的中心问题是求解线性方程组。线性的意思是这些方程的未知数是一次的,即每个未知数只会乘数字,而不会出现 x x x 与 y y y 相乘的项。下面是一个由两个未知数组成的方程组: 两个方程 两个未知数 { x − 2 y = 1 3 x + 2 y = 11 ( 2.1.1 ) \begin{matrix}\textbf{两个方程}\kern 11pt\\\textbf{两个未知数}\end{matrix}\kern 15pt\left\{\begin{matrix}x-2y=1\\3x+2y=11\end{matrix}\right.\kern 20pt(2.1.1) 两个方程两个未知数{x−2y=13x+2y=11(2.1.1)我们首先一次处理一行。将这两个方程的图像在 x y xy xy 平面上画出来,如Figrure 2.1所示。行图像中第一条直线是 x − 2 y = 1 x-2y=1 x−2y=1,第二条直线是 3 x + 2 y = 11 3x+2y=11 3x+2y=11,它们的交点是 x = 3 , y = 1 x=3,y=1 x=3,y=1,点 ( 3 , 1 ) (3,1) (3,1) 同时落在两条直线上,也是两个方程的解。
下面考虑列图像,将上述方程组写成 “向量方程式”,我们要观察的是向量而不是数字。向量方程式表示列的组合: 列的组合等于 b x [ 1 3 ] + y [ − 2 2 ] = [ 1 11 ] = b ( 2.1.2 ) \textbf{列的组合等于}\,\boldsymbol b\kern 15ptx\begin{bmatrix}1\\3\end{bmatrix}+y\begin{bmatrix}-2\\\kern 7pt2\end{bmatrix}=\begin{bmatrix}1\\11\end{bmatrix}=\boldsymbol b\kern 20pt(2.1.2) 列的组合等于bx[13]+y[−22]=[111]=b(2.1.2)左侧有两个列向量,问题是找到这些向量正确的组合使得它们与右侧的向量相等。第一列乘 x x x,第二列乘 y y y,然后将它们相加。正确的组合是 x = 3 x=3 x=3, y = 1 y=1 y=1(与行图像得到的结果相同), 3 ( 列1 ) + 1 ( 列2 ) = b 3(\textbf{列1})+1(\textbf{列2})=\boldsymbol b 3(列1)+1(列2)=b。

列:列图像组合左侧的列向量产生右侧的向量 b \boldsymbol b b。
Figure 2.2 是两个方程两个未知数的列图像,第一个图是两个不同的列,然后第一列乘 3 3 3,数乘是线性代数中两个基本运算之一: 数乘 3 [ 1 3 ] = [ 3 9 ] \textbf{数乘}\kern 20pt3\begin{bmatrix}1\\3\end{bmatrix}=\begin{bmatrix}3\\9\end{bmatrix} 数乘3[13]=[39]如果向量 v \boldsymbol v v 的分量是 v 1 v_1 v1 与 v 2 v_2 v2,则 c v c\boldsymbol v cv 的分量是 c v 1 cv_1 cv1 与 c v 2 cv_2 cv2。
另一个基本运算是向量的加法,分别将两个向量的第一分量和第二分量相加,其和是 ( 1 , 11 ) (1,11) (1,11),即 b \boldsymbol b b: 向量加法 [ 3 9 ] + [ − 2 2 ] = [ 1 11 ] \textbf{向量加法}\kern 20pt\begin{bmatrix}3\\9\end{bmatrix}+\begin{bmatrix}-2\\\kern 7pt2\end{bmatrix}=\begin{bmatrix}1\\11\end{bmatrix} 向量加法[39]+[−22]=[111]Figure 2.2 中的第二个图表示上述的向量加法。黑线表示两个向量,其对角线表示两个向量的和,也就是线性方程组右侧的向量 b = ( 1 , 11 ) \boldsymbol b=(1,11) b=(1,11)。
重复一遍:向量方程式的左侧是列的线性组合,问题是找到正确的系数 x = 3 , y = 1 x=3,y=1 x=3,y=1。将数乘和向量的加法合成一个步骤,这个步骤非常重要,因为它包含了两个基本运算:向量的两列分别乘 3 3 3 和 1 1 1,然后相加。 线性组合 3 [ 1 3 ] + [ − 2 2 ] = [ 1 11 ] \textbf{线性组合}\kern 20pt3\begin{bmatrix}1\\3\end{bmatrix}+\begin{bmatrix}-2\\\kern 7pt2\end{bmatrix}=\begin{bmatrix}1\\11\end{bmatrix} 线性组合3[13]+[−22]=[111]方程组左侧的系数矩阵是一个 2 × 2 2×2 2×2 的矩阵 A A A: 系数矩阵 A = [ 1 − 2 3 2 ] \textbf{系数矩阵}\kern 20ptA=\begin{bmatrix}1&-2\\3&\kern 7pt2\end{bmatrix} 系数矩阵A=[13−22]我们可以从行或者列来观察矩阵,行可以得到行图像,列可以得到列图像。相同的方程组,可以通过不同的图像来观察。方程组写成矩阵方程式 A x = b A\boldsymbol x=\boldsymbol b Ax=b: 矩阵方程式 A x = b [ 1 − 2 3 2 ] [ x y ] = [ 1 11 ] \textbf{矩阵方程式}\,A\boldsymbol x=\boldsymbol b\kern 20pt\begin{bmatrix}1&-2\\3&\kern 7pt2\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}1\\11\end{bmatrix} 矩阵方程式Ax=b[13−22][xy]=[111]行图像处理两行,列图像组合两列。将 x = 3 , y = 1 x=3,y=1 x=3,y=1 代入 x \boldsymbol x x,即矩阵-向量的乘法: { 行的点积 列的组合 A x = b [ 1 − 2 3 2 ] [ 3 1 ] = [ 1 11 ] \left\{\begin{matrix}\textbf{行的点积}\\\textbf{列的组合}\end{matrix}\right.\kern 10ptA\boldsymbol x=\boldsymbol b\kern 10pt\begin{bmatrix}1&-2\\3&\kern 7pt2\end{bmatrix}\begin{bmatrix}3\\1\end{bmatrix}=\begin{bmatrix}1\\11\end{bmatrix} {行的点积列的组合Ax=b[13−22][31]=[111]
二、三个未知数三个方程
下面讨论三个未知数,三个方程的情况,未知数是 x , y , z x,y,z x,y,z,线性方程如下: A x = b { x + 2 y + 3 z = 6 2 x + 5 y + 2 z = 4 6 x − 3 y + z = 2 ( 2.1.3 ) A\boldsymbol x=\boldsymbol b\kern 20pt\left\{\begin{matrix}x+2y+3z=6\\2x+5y+2z=4\\6x-3y+z=2\end{matrix}\right.\kern 20pt(2.1.3) Ax=b⎩ ⎨ ⎧x+2y+3z=62x+5y+2z=46x−3y+z=2(2.1.3)方程组的解可能存在也可能不存在,本例中是有解的。一般情况下,当未知数的个数等于方程的个数时(例如本例中),通常会有一个解。
我们首先从两个方面来观察本例:
行: 行图像显示三个平面相交于一点。
列: 列图像三个列的组合产生 b = ( 6 , 4 , 2 ) \boldsymbol b=(6,4,2) b=(6,4,2)。
在行图像中,每个方程表示一个三维空间中的平面,Figure 2.3 中的第一个平面表示 x + 2 y + 3 z = 6 x+2y+3z=6 x+2y+3z=6,该平面与 x , y , z x,y,z x,y,z 轴的交点分别是 ( 6 , 0 , 0 ) (6,0,0) (6,0,0), ( 0 , 3 , 0 ) (0,3,0) (0,3,0), ( 0 , 0 , 2 ) (0,0,2) (0,0,2),这三个点都满足这个方程,且确定一个平面。
由于向量 ( x , y , z ) = ( 0 , 0 , 0 ) (x,y,z)=(0,0,0) (x,y,z)=(0,0,0) 不是 x + 2 y + 3 z = 6 x+2y+3z=6 x+2y+3z=6 的解,所该平面不过原点。平面 x + 2 y + 3 z = 0 x+2y+3z=0 x+2y+3z=0 过原点,且平行于 x + 2 y + 3 z = 6 x+2y+3z=6 x+2y+3z=6。
第二个平面表示 2 x + 5 y + 2 z = 4 2x+5y+2z=4 2x+5y+2z=4,它与第一个平面交于一条直线 L L L。一般来说三个未知数两个方程的通解是一条直线,如本例的直线 L L L。(但是方程 x + 2 y + 3 z = 6 x+2y+3z=6 x+2y+3z=6 和 x + 2 y + 3 z = 0 x+2y+3z=0 x+2y+3z=0 没用通解,它们在空间中表示的两个平面平行。)
第三个平面表示 6 x − 3 y + z = 2 6x-3y+z=2 6x−3y+z=2,它与直线 L L L 相交于一点,这个点落在全部三个平面上,就是三个方程的解。它们的交点是 ( 0 , 0 , 2 ) (0,0,2) (0,0,2),这个在行图像中很难看出。

列图像我们写成向量的形式 A x = b A\boldsymbol x=\boldsymbol b Ax=b: 列的组合 x [ 1 2 6 ] + y [ 2 5 − 3 ] + z [ 3 2 1 ] = [ 6 4 2 ] = b ( 2.1.4 ) \textbf{列的组合}\kern 12ptx\begin{bmatrix}1\\2\\6\end{bmatrix}+y\begin{bmatrix}\kern 7pt2\\\kern 7pt5\\-3\end{bmatrix}+z\begin{bmatrix}3\\2\\1\end{bmatrix}=\begin{bmatrix}6\\4\\2\end{bmatrix}=\boldsymbol b\kern 15pt(2.1.4) 列的组合x 126 +y 25−3 +z 321 = 642 =b(2.1.4)未知数是系数 x , y , z x,y,z x,y,z,我们需要对三个列向量进行正确的组合,产生 b = ( 6 , 4 , 2 ) \boldsymbol b=(6,4,2) b=(6,4,2)。
Figure 2.4 是本例的列图像,这些列向量的线性组合可以产生任意的 b \boldsymbol b b !当 b = ( 6 , 4 , 2 ) \boldsymbol b=(6,4,2) b=(6,4,2) 时,需要的组合是第三列乘 2 2 2,系数为 x = 0 , y = 0 , z = 2 x=0,y=0,z=2 x=0,y=0,z=2。
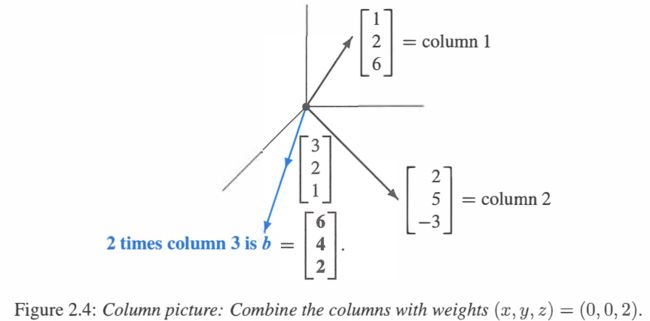
行图像中的三个平面也是相交于这一点 ( 0 , 0 , 2 ) (0,0,2) (0,0,2),这个点就是列的正确组合: 正确组合 ( x , y , z ) = ( 0 , 0 , 2 ) 0 [ 1 2 6 ] + 0 [ 2 5 − 3 ] + 2 [ 3 2 1 ] = [ 6 4 2 ] 正确组合(x,y,z)=(0,0,2)\kern 16pt0\begin{bmatrix}1\\2\\6\end{bmatrix}+0\begin{bmatrix}\kern 7pt2\\\kern 7pt5\\-3\end{bmatrix}+2\begin{bmatrix}3\\2\\1\end{bmatrix}=\begin{bmatrix}6\\4\\2\end{bmatrix} 正确组合(x,y,z)=(0,0,2)0 126 +0 25−3 +2 321 = 642
三、方程组的矩阵形式
行图像中有三行,列图像中有三列,三行三列有 9 9 9 个数字,它们形成一个 3 × 3 3\times3 3×3 的矩阵 A A A: A x = b 的系数矩阵 A = [ 1 2 3 2 5 2 6 − 3 1 ] A\boldsymbol x=\boldsymbol b\,的系数矩阵\kern 15ptA=\begin{bmatrix}1&2&3\\2&5&2\\6&-3&1\end{bmatrix} Ax=b的系数矩阵A= 12625−3321 大写字母 A A A 代表这 9 9 9 个数,它们形成一个方阵,字母 b \boldsymbol b b 表示列向量,它的分量是 6 , 4 , 2 6,4,2 6,4,2。未知数 x \boldsymbol x x 也是一个列向量,它的分量是 x , y , z x,y,z x,y,z。(我们用粗体字母表示向量)。对于方程组,我们可以以三种形式来看,式(2.1.3)是行形式;式(2.1.4)是列形式;式(2.1.5)是矩阵形式: 矩阵方程 A x = b [ 1 2 3 2 5 2 6 − 3 1 ] [ x y z ] = [ 6 4 2 ] ( 2.1.5 ) 矩阵方程\,A\boldsymbol x=\boldsymbol b\kern 15pt\begin{bmatrix}1&2&3\\2&5&2\\6&-3&1\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}6\\4\\2\end{bmatrix}\kern 10pt(2.1.5) 矩阵方程Ax=b 12625−3321 xyz = 642 (2.1.5)下面讨论一个问题: A A A 乘 x \boldsymbol x x 的意义?
x \boldsymbol x x 可以被行乘,也可以被列乘,它们是同样东西以不同形式来理解。
被行乘: A x 代表 点积 ,每个行乘列 x A x = [ ( r o w 1 ) ⋅ x ( r o w 2 ) ⋅ x ( r o w 3 ) ⋅ x ] ( 2.1.6 ) A\boldsymbol x\,代表\textbf{点积},每个行乘列\,\boldsymbol x\kern 15ptA\boldsymbol x=\begin{bmatrix}(row\,1)\cdot\boldsymbol x\\(row\,2)\cdot\boldsymbol x\\(row3)\cdot\boldsymbol x\end{bmatrix}\kern 10pt(2.1.6) Ax代表点积,每个行乘列xAx= (row1)⋅x(row2)⋅x(row3)⋅x (2.1.6)
被列乘: A x 是 列向量的线性组合 A x = x ( c o l u m n 1 ) + y ( c o l u m n 2 ) + z ( c o l u m n 3 ) ( 2.1.7 ) A\boldsymbol x\,是\textbf{列向量的线性组合}\kern 11ptA\boldsymbol x=x(column\,1)+y(column\,2)+z(column\,3)\kern 11pt(2.1.7) Ax是列向量的线性组合Ax=x(column1)+y(column2)+z(column3)(2.1.7)将解 x = ( 0 , 0 , 2 ) \boldsymbol x=(0,0,2) x=(0,0,2) 代入 A x A\boldsymbol x Ax 将产生 b \boldsymbol b b: [ 1 2 3 2 5 2 6 − 3 1 ] [ 0 0 2 ] = 2 × ( c o l u m n 3 ) = [ 6 4 2 ] \begin{bmatrix}1&2&3\\2&5&2\\6&-3&1\end{bmatrix}\begin{bmatrix}0\\0\\2\end{bmatrix}=2\times(column\,3)=\begin{bmatrix}6\\4\\2\end{bmatrix} 12625−3321 002 =2×(column3)= 642 用行形式来解释,则第一行的点积 ( 1 , 2 , 3 ) ⋅ ( 0 , 0 , 2 ) = 6 (1,2,3)\cdot(0,0,2)=6 (1,2,3)⋅(0,0,2)=6,第二行的点积 ( 2 , 5 , 2 ) ⋅ ( 0 , 0 , 2 ) = 4 (2,5,2)\cdot(0,0,2)=4 (2,5,2)⋅(0,0,2)=4,第三行的点积 ( 6 , − 3 , 1 ) ⋅ ( 0 , 0 , 2 ) = 2 (6,-3,1)\cdot(0,0,2)=2 (6,−3,1)⋅(0,0,2)=2。用列形式来解释,则 b \boldsymbol b b 为第三列的 2 2 2 倍。今后主要将 A x A\boldsymbol x Ax 当做是 A A A 列的组合。
【例1】 3 × 3 3\times3 3×3 的矩阵 A A A 和单位矩阵 I I I: A x = [ 1 0 0 1 0 0 1 0 0 ] [ 4 5 6 ] = [ 4 4 4 ] I x = [ 1 0 0 0 1 0 0 0 1 ] [ 4 5 6 ] = [ 4 5 6 ] A\boldsymbol x=\begin{bmatrix}1&0&0\\1&0&0\\1&0&0\end{bmatrix}\begin{bmatrix}4\\5\\6\end{bmatrix}=\begin{bmatrix}4\\4\\4\end{bmatrix}\kern 10ptI\boldsymbol x=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\begin{bmatrix}4\\5\\6\end{bmatrix}=\begin{bmatrix}4\\5\\6\end{bmatrix} Ax= 111000000 456 = 444 Ix= 100010001 456 = 456 通过行形式和列形式都可以得出结果。
单位矩阵 I I I 的主对角线都是 1 1 1,这个矩阵乘任何向量都是原来的向量,就像 1 1 1 乘上任何数一样,不同的是现在是矩阵乘向量。本例中的 I I I 是 3 × 3 3\times3 3×3 的单位矩阵: I = [ 1 0 0 0 1 0 0 0 1 ] I x = x 总成立 I=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\kern 10ptI\boldsymbol x=\boldsymbol x\,总成立 I= 100010001 Ix=x总成立
四、矩阵表示法
一个 2 × 2 2\times2 2×2 的矩阵的第一行是 a 11 a_{11} a11 和 a 12 a_{12} a12,第二行是 a 21 a_{21} a21 和 a 22 a_{22} a22。第一个下标表示行数,第二个下标表示列数,所以 a i j a_{ij} aij 是第 i i i 行第 j j j 列的单元。由于下标不方便打出来,所以 a i j a_{ij} aij 也可以用 A ( i , j ) A(i,j) A(i,j) 来表示。例如单元 a 57 = A ( 5 , 7 ) a_{57}=A(5,7) a57=A(5,7) 就在第 5 5 5 行,第 7 7 7 列。 A = [ a 11 a 12 a 21 a 22 ] = [ A ( 1 , 1 ) A ( 1 , 2 ) A ( 2 , 1 ) A ( 2 , 2 ) ] A=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}=\begin{bmatrix}A(1,1)&A(1,2)\\A(2,1)&A(2,2)\end{bmatrix} A=[a11a21a12a22]=[A(1,1)A(2,1)A(1,2)A(2,2)]对于 m × n m\times n m×n 的矩阵,行的下标 i i i 从 1 1 1 到 m m m,列的下表 j j j 从 1 1 1 到 n n n,它共有 m n mn mn 个单元 a i j = A ( i , j ) a_{ij}=A(i,j) aij=A(i,j),一个 n n n 阶的方形矩阵有 n 2 n^2 n2 个单元。
五、MATLAB 中的矩阵乘法
定义矩阵 A A A 和 列向量 x \boldsymbol x x,其中 R n R^n Rn ( n n n 维空间)中的向量 x \boldsymbol x x 表示一个 n × 1 n\times1 n×1 的矩阵,输入矩阵时每次输入一行,用分号 ; 表示一行的结束。输入列向量 x \boldsymbol x x 可以直接以列形式输入,也可以用行形式输入,然后用 ’ 表示转置:

在 MATLAB 中有三种方法可以得到 A x A\boldsymbol x Ax:
(1)可以直接使用 MATLAB 语言得到矩阵乘法:
b = A ∗ x b=A*x b=A∗x
(2)一次处理一行,即点积的形式:选出 A A A 的每一行,将其视为 1 × 3 1\times3 1×3 的矩阵,可以表示为 A ( 1 , : ) A(1,:) A(1,:)。在这里冒号 : 代表一行的全部列。
b = [ A ( 1 , : ) ∗ x ; A ( 2 , : ) ∗ x ; A ( 3 , : ) ∗ x ] b=[A(1,:)*x;\,A(2,:)*x;\,A(3,:)*x] b=[A(1,:)∗x;A(2,:)∗x;A(3,:)∗x]
(3)一次处理一列,即列的线性组合。第一列是 3 × 1 3\times1 3×1 的子矩阵 A ( : , 1 ) A(:,1) A(:,1),这里冒号 : 代表一列的全部行。
b = A ( : , 1 ) ∗ x ( 1 ) + A ( : , 2 ) ∗ x ( 2 ) + A ( : , 3 ) ∗ x ( 3 ) b=A(:,1)*x(1)+A(:,2)*x(2)+A(:,3)*x(3) b=A(:,1)∗x(1)+A(:,2)∗x(2)+A(:,3)∗x(3)
MATLAB 中 A ∗ x A*x A∗x 是用列的形式来实现的。
六、主要内容总结
- 向量的基本运算是数乘 c v c\boldsymbol v cv 和向量的加法 v + w \boldsymbol v+\boldsymbol w v+w。
- 将向量的数乘与加法相结合可以得到线性组合 c v + d w c\boldsymbol v+d\boldsymbol w cv+dw。
- 矩阵 – 向量的乘法 A x A\boldsymbol x Ax 可以由点积得到,一次处理一行;也可以由 A A A 的列的线性组合得到,一次处理一列。
- 列图像: A x = b A\boldsymbol x=\boldsymbol b Ax=b 是找到列的线性组合产生 b \boldsymbol b b。
- 行图形: A x = b A\boldsymbol x=\boldsymbol b Ax=b 的每个方程会得到一条直线( n = 2 n=2 n=2),或一个平面( n = 3 n=3 n=3)或一个超平面( n > 3 n>3 n>3)。如果仅有一个解会相交于一点,若有很多解,会相交成直线、平面、或超平面。
七、例题
【例2】描述三个方程 A x = b A\boldsymbol x=\boldsymbol b Ax=b 的列图像,仔细观察列(不使用消元法)求解: { x + 3 y + 2 z = − 3 2 x + 2 y + 2 z = − 2 3 x + 5 y + 6 z = − 5 [ 1 3 2 2 2 2 3 5 6 ] = [ x y z ] = [ − 3 − 2 − 5 ] \left\{\begin{matrix}x+3y+2z=-3\\2x+2y+2z=-2\\3x+5y+6z=-5\end{matrix}\right.\kern 15pt\begin{bmatrix}1&3&2\\2&2&2\\3&5&6\end{bmatrix}=\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}-3\\-2\\-5\end{bmatrix} ⎩ ⎨ ⎧x+3y+2z=−32x+2y+2z=−23x+5y+6z=−5 123325226 = xyz = −3−2−5 解: 列图像是寻找 A A A 三个列正确的线性组合产生 b \boldsymbol b b。通过观察可以发现, b \boldsymbol b b 是第二列的相反数,所以可得 x = 0 , y = − 1 , z = 0 x=0,y=-1,z=0 x=0,y=−1,z=0。若是要证明 ( 0 , − 1 , 0 ) (0,-1,0) (0,−1,0) 是唯一解,需要确认 A A A 可逆,三个列之间是无关的,行列式不为 0 0 0。
【例3】下面的系统无解。行图像中的平面并没有相交于一点。即并不存在三个列的线性组合可以产生 b \boldsymbol b b。 { x + 3 y + 5 z = 4 x + 2 y − 3 z = 5 2 x + 5 y + 2 z = 8 [ 1 3 5 1 2 − 3 2 5 2 ] [ x y z ] = [ 4 5 8 ] = b \left\{\begin{matrix}x+3y+5z=4\\x+2y-3z=5\\2x+5y+2z=8\end{matrix}\right.\kern 15pt\begin{bmatrix}1&3&5\\1&2&-3\\2&5&2\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}4\\5\\8\end{bmatrix}=\boldsymbol b ⎩ ⎨ ⎧x+3y+5z=4x+2y−3z=52x+5y+2z=8 1123255−32 xyz = 458 =b(方程 1 1 1)+(方程2)-(方程3)可得 0 = 1 0=1 0=1,所以该系统无解。向量 ( 1 , 1 , − 1 ) (1,1,-1) (1,1,−1) 与 A A A 的三个列均正交(orthogonal),但是与 b \boldsymbol b b 不正交。
(1)三个平面中存在两个互相平行的平面吗?什么方程与平面 x + 3 y + 5 z = 4 x+3y+5z=4 x+3y+5z=4 平行?
(2)计算 A A A 每一列与 y = ( 1 , 1 , − 1 ) \boldsymbol y=(1,1,-1) y=(1,1,−1) 的点积, b \boldsymbol b b 与 y \boldsymbol y y 的点积。这些点积如何能表明 A A A 列的线性组合无法产生 b \boldsymbol b b?
(3)求出右侧三个不同的向量 b ∗ , b ∗ ∗ , b ∗ ∗ ∗ \boldsymbol b^*,\boldsymbol b^{**},\boldsymbol b^{***} b∗,b∗∗,b∗∗∗,使得方程有解。
解:(1)这三个平面中没有两个平行的平面,它们也没有相交于一点(如下图)。将 4 4 4 改成任意实数都可以得到与 x + 3 y + 5 z = 4 x+3y+5z=4 x+3y+5z=4 平行的平面,例如 x + 3 y + 5 z = 0 x+3y+5z=0 x+3y+5z=0 是一个过原点 ( 0 , 0 , 0 ) (0,0,0) (0,0,0) 的平面。

(2) A A A 的每一列与 y \boldsymbol y y 的点积都为 0 0 0。 y ⋅ b = ( 1 , 1 , − 1 ) ⋅ ( 4 , 5 , 8 ) = 1 \boldsymbol y\cdot\boldsymbol b=(1,1,-1)\cdot(4,5,8)=1 y⋅b=(1,1,−1)⋅(4,5,8)=1 不为 0 0 0,代入 A x = b A\boldsymbol x=\boldsymbol b Ax=b 可得 0 = 1 0=1 0=1,这是不可能的,所以无解,也就表明 A A A 列的线性组合无法产生 b \boldsymbol b b。
(3)当 b \boldsymbol b b 是 A A A 列的线性组合时,则有解。当对应的解 x ∗ = ( 1 , 0 , 0 ) \boldsymbol x^{*}=(1,0,0) x∗=(1,0,0), x ∗ ∗ = ( 1 , 1 , 1 ) \boldsymbol x^{**}=(1,1,1) x∗∗=(1,1,1), x ∗ ∗ ∗ = ( 0 , 0 , 0 ) \boldsymbol x^{***}=(0,0,0) x∗∗∗=(0,0,0) 时可以得到: b ∗ = [ 1 1 2 ] b ∗ ∗ = [ 9 0 9 ] b ∗ ∗ ∗ = [ 0 0 0 ] \boldsymbol b^*=\begin{bmatrix}1\\1\\2\end{bmatrix}\kern 10pt\boldsymbol b^{**}=\begin{bmatrix}9\\0\\9\end{bmatrix}\kern 10pt\boldsymbol b^{***}=\begin{bmatrix}0\\0\\0\end{bmatrix} b∗= 112 b∗∗= 909 b∗∗∗= 000

