ORB_SLAM3中IMU预积分过程原理分析

ORB_SLAM3中IMU预积分过程原理分析

1. 特殊正交群SO(3)的一些性质

指数映射:
$$exp({\varphi }^{\hat{}})=\mathbf{I}+\frac{sin(\Vert \varphi \Vert )}{\Vert \varphi \Vert }{\varphi }^{\hat{}}+\frac{1-cos(\Vert \varphi \Vert )}{{\Vert \varphi \Vert }^2}({\varphi }^{\hat{}}{)}^2\text{\hspace{1em}(1)}$$
指数映射的一阶近似:
$$exp({\varphi }^{\hat{}})\approx \mathbf{I}+{\varphi }^{\hat{}}\text{\hspace{1em}(2)}$$
对数映射:
$$log(\mathbf{R})=\frac{\phi \cdot (\mathbf{R}-{\mathbf{R}}^T)}{2sin(\phi )}其中\phi =co{s}^{-1}(\frac{tr(\mathbf{R})-1}{2})\text{\hspace{1em}(3)}$$
BCH公式与近似形式(14讲72页):
$$Exp(\varphi +\delta \varphi )\approx Exp(\varphi )Exp({\mathbf{J}}_r(\varphi )\delta \varphi )\text{\hspace{1em}(4)}$$
式4中:
$${\mathbf{J}}_r(\varphi )=\mathbf{I}-\frac{1-cos(\Vert \varphi \Vert )}{{\Vert \varphi \Vert }^2}+\frac{\Vert \varphi \Vert -sin(\Vert \varphi \Vert )}{\Vert {\varphi }^3\Vert }({\varphi }^{\hat{}}{)}^2\text{\hspace{1em}(5)}$$
指数映射还有如下性质:
$$Exp(\varphi )\mathbf{R}=\mathbf{R}Exp({\mathbf{R}}^T\varphi )\text{\hspace{1em}(6)}$$
注: 上述为了公式的简便使用了 $Exp(\varphi )$ 代替了 $exp({\varphi }^{\hat{}})$.

2. IMU测量模型和运动模型

测量模型:
$$\begin{array}{rl}{}_{{}_B}{\mathbf{\omega }}_{{}_{WB}}(t)& ={}_{{}_B}{\mathbf{\omega }}_{{}_{WB}}(t)+{\mathbf{b}}^g(t)+{\mathbf{\eta }}^g(t)\\ {}_{{}_B}\mathbf{a}(t)& ={\mathbf{R}}_{{}_{WB}}^T({}_{{}_W}\mathbf{a}(t)-{}_{{}_W}\mathbf{g})+{\mathbf{b}}^a(t)+{\mathbf{\eta }}^a(t)\end{array}\text{\hspace{1em}(7)}$$
运动学模型:
$$\begin{array}{rl}{\dot{\mathbf{R}}}_{{}_{WB}}& ={\mathbf{R}}_{{}_{WB}}\cdot {}_{{}_B}{\mathbf{\omega }}_{{}_{WB}}\hat{}\\ {\dot{\mathbf{v}}}_{{}_W}& ={}_{{}_W}\mathbf{a}\\ {\dot{\mathbf{p}}}_{{}_W}& ={}_{{}_W}\mathbf{v}\end{array}\text{\hspace{1em}(8)}$$
基于运动学模型可得 $t$ 和 $t+\Delta t$ 时刻状态关系:
$$\begin{array}{rl}{\mathbf{R}}_{{}_{WB}}(t+\Delta t)& ={\mathbf{R}}_{{}_{WB}}Exp{\int }_t^{t+\Delta t}{}_{{}_B}{\mathbf{\omega }}_{{}_{WB}}(\tau )d\tau \\ {}_{{}_W}\mathbf{v}(t+\Delta t)& ={}_{{}_W}\mathbf{v}(t)+{\int }_t^{t+\Delta t}{}_{{}_W}\mathbf{a}(\tau )d\tau \\ {}_{{}_W}\mathbf{p}(t+\Delta t)& ={}_{{}_W}\mathbf{p}(t)+{\int }_t^{t+\Delta t}{}_{{}_W}\mathbf{v}(\tau )d\tau +{\iint }_t^{t+\Delta t}{}_{{}_W}\mathbf{a}(\tau )d{\tau }^2\end{array}\text{\hspace{1em}(9)}$$
假设 ${}_{{}_W}\mathbf{a}$ 和 ${}_{{}_B}{\mathbf{\omega }}_{{}_{WB}}$ 在 $[t,t+\Delta t]$区间内不变，则公式(9)的结果:
$$\begin{array}{rl}{\mathbf{R}}_{{}_{WB}}(t+\Delta t)& ={\mathbf{R}}_{{}_{WB}}Exp({}_{{}_B}{\mathbf{\omega }}_{{}_{WB}}(t)\Delta t)\\ {}_{{}_W}\mathbf{v}(t+\Delta t)& ={}_{{}_W}\mathbf{v}(t)+{}_{{}_W}\mathbf{a}(t)\Delta t\\ {}_{{}_W}\mathbf{p}(t+\Delta t)& ={}_{{}_W}\mathbf{p}(t)+{}_{{}_W}\mathbf{v}(t)\Delta t+\frac{1}{2}{}_{{}_W}\mathbf{a}(t){\Delta t}^2\end{array}\text{\hspace{1em}(10)}$$
将公式(7)测量模型带入公式(10)可得:
$$\begin{array}{rl}\mathbf{R}(t+\Delta t)& =\mathbf{R}(t)Exp((\mathbf{\omega }(t)-{\mathbf{b}}^g(t)-{\mathbf{\eta }}^{gd}(t))\Delta t)\\ \mathbf{v}(t+\Delta t)& =\mathbf{v}(t)+\mathbf{g}\Delta t+\mathbf{R}(t)(\mathbf{a}(t)-{\mathbf{b}}^a(t)-{\mathbf{\eta }}^{ad}(t))\Delta t\\ \mathbf{p}(t+\Delta t)& =\mathbf{p}(t)+\mathbf{v}(t)\Delta t+\frac{1}{2}\mathbf{g}\Delta t^2+\frac{1}{2}\mathbf{R}(t)(\mathbf{a}(t)-{\mathbf{b}}^a(t)-{\mathbf{\eta }}^{ad}(t))\Delta t^2\end{array}\text{\hspace{1em}(11)}$$
注: 上述推导从公式(9)开始就假设$R_{{}_{WB}}(t)$在$[t,\Delta t]$区间内是不变的，这与VINS预积分的推导是不一样的，这样的假设最大的好处就是使得公式比较简洁。另外是由于在视觉惯性紧耦合的slam算法中使用的imu频率都比较高，因此假设相邻两帧之间的位姿没有变化也是较合理的，并且参考论文中的作者也在实际实验中验证了该假设并不会明显影响算法测试结果。但如果使用的imu频率较低，就不能这么假设。

3. IMU预积分

所谓的预积分过程就是将两关键帧之间的所有imu测量值转换成一个测量值，这样就可以只加入一个观测约束，减少了约束数量，可有效的保证vio过程的实时进行。假设两相邻关键帧获取时刻采集的imu帧索引为i和j。则j时刻的状态信息可由i时刻状态信息通过如下积分获得:
$$\begin{array}{rl}{\mathbf{R}}_j& ={\mathbf{R}}_i\prod _{k=i}^{j-1}Exp(({\mathbf{w}}_k-{\mathbf{b}}_k^g-{\mathbf{\eta }}_k^{gd})\Delta t)\\ {\mathbf{v}}_j& ={\mathbf{v}}_i+\mathbf{g}\Delta t_{ij}+\sum _{k=i}^{j-1}{\mathbf{R}}_k({\mathbf{a}}_k-{\mathbf{b}}_k^a-{\mathbf{\eta }}_k^{ad})\Delta t\\ {\mathbf{p}}_j& ={\mathbf{p}}_i+\sum _{k=i}^{j-1}[{\mathbf{v}}_k\Delta t+\frac{1}{2}\mathbf{g}\Delta t^2+\frac{1}{2}{\mathbf{R}}_k({\mathbf{a}}_k-{\mathbf{b}}_k^a-{\mathbf{\eta }}_k^{ad})\Delta t^2]\end{array}\text{\hspace{1em}(12)}$$
上面公式(12)有个缺点就是如果在 $t_i$ 时刻的状态 $[{\mathbf{p}}_i,{\mathbf{v}}_i,{\mathbf{R}}_i,{\mathbf{b}}_i^a,{\mathbf{b}}_i^g]$ 发生改变(在进行vio轨迹优化时，状态会不断的进行调整)，则需要重新重复上面的积分过程，这将非常耗时，为了避免该问题，对上述积分过程进行了如下改变:
$$\begin{array}{rl}\Delta {\mathbf{R}}_{ij}& ={\mathbf{R}}_i^T{\mathbf{R}}_j=\prod _{k=i}^{j-1}Exp(({\mathbf{w}}_k-{\mathbf{b}}_k^g-{\mathbf{\eta }}_k^{gd})\Delta t)\\ \Delta {\mathbf{v}}_{ij}& ={\mathbf{R}}_i^T({\mathbf{v}}_j-{\mathbf{v}}_i-\mathbf{g}\Delta t_{ij})=\sum _{k=i}^{j-1}{\mathbf{R}}_{ik}({\mathbf{a}}_k-{\mathbf{b}}_k^a-{\mathbf{\eta }}_k^{ad})\Delta t\\ \Delta {\mathbf{p}}_{ij}& ={\mathbf{R}}_i^T({\mathbf{p}}_j-{\mathbf{p}}_i-\frac{1}{2}\mathbf{g}\Delta t_{ij}^2)=\sum _{k=i}^{j-1}[{\mathbf{v}}_{ik}\Delta t+\frac{1}{2}{\mathbf{R}}_{ik}({\mathbf{a}}_k-{\mathbf{b}}_k^a-{\mathbf{\eta }}_k^{ad})\Delta t^2]\end{array}\text{\hspace{1em}(13)}$$
从公式(13)可以看出右边积分部分只与$[{\mathbf{b}}_i^a,{\mathbf{b}}_i^g]$ 状态有关，按当前的公式来说，偏置发生改变，右侧的积分过程需要重新进行，但由于偏置变化较小，可以用近似的方法来计算，后面3.3节会专门来说这个问题。

3.1 预积分测量模型

3.1.1 姿态测量模型

由公式(13)，可知:
$$\begin{array}{rl}\Delta {\mathbf{R}}_{ij}& ={\mathbf{R}}_i^T{\mathbf{R}}_j\\ & =\prod _{k=i}^{j-1}Exp(({\mathbf{w}}_k-{\mathbf{b}}_k^g-{\mathbf{\eta }}_k^{gd})\Delta t)\\ & \stackrel{(4)}{\simeq }\prod _{k=i}^{j-1}Exp(({\mathbf{w}}_k-{\mathbf{b}}_k^g)\Delta t)Exp(-{\mathbf{J}}_r^k(({\mathbf{w}}_k-{\mathbf{b}}_k^g)\Delta t){\mathbf{\eta }}_k^{gd}\Delta t)\\ & \stackrel{(6)}{=}\Delta {\mathbf{R}}_{ij}\prod _{k=i}^{j-1}Exp(-\Delta {\mathbf{R}}_{k+1,j}^T{\mathbf{J}}_r^k(({\mathbf{w}}_k-{\mathbf{b}}_k^g)\Delta t){\mathbf{\eta }}_k^{gd}\Delta t)\\ & =\Delta {\mathbf{R}}_{ij}Exp(-\delta {\varphi }_{ij})\end{array}\text{\hspace{1em}(14)}$$
式中:
$$\Delta {\mathbf{R}}_{ij}=\prod _{k=i}^{j-1}Exp(({\mathbf{w}}_k-{\mathbf{b}}_k^g)\Delta t)$$
上述推导中最难的部分是获得第二步结果，其推导方式可参考博客 。 于是基于公式(14)可获得姿态测量方程为:
$$\Delta {\mathbf{R}}_{ij}={\mathbf{R}}_i^T{\mathbf{R}}_{j}Exp(\delta {\varphi }_{ij})\text{\hspace{1em}(15)}$$
注: 式中(4)(6)指的是基于公式(4)(6)来推导的，后面都会用这种表示方式.

3.1.2 速度测量模型

将公式(14)结果 $\Delta {\mathbf{R}}_{ij}=\Delta {\mathbf{R}}_{ij}Exp(-\delta {\varphi }_{ij})$带入公式(13)的$\Delta {\mathbf{v}}_{ij}$中可得:
$$\begin{array}{rl}\Delta {\mathbf{v}}_{ij}& ={\mathbf{R}}_i^T({\mathbf{v}}_j-{\mathbf{v}}_i-\mathbf{g}\Delta t_{ij})\\ & =\sum _{k=i}^{j-1}{\mathbf{R}}_{ik}({\mathbf{a}}_k-{\mathbf{b}}_k^a-{\mathbf{\eta }}_k^{ad})\Delta t\\ & \stackrel{(2,14)}{\simeq }\sum _{k=i}^{j-1}\Delta {\mathbf{R}}_{ik}(\mathbf{I}-\delta {\varphi }_{ik}\hat{})({\mathbf{a}}_k-{\mathbf{b}}_i^a)\Delta t-\Delta {\mathbf{R}}_{ik}{\mathbf{\eta }}_k^{ad}\Delta t\\ & =\Delta {\mathbf{v}}_{ij}+\sum _{k=i}^{j-1}[\Delta {\mathbf{R}}_{ik}({\mathbf{a}}_k-{\mathbf{b}}_i^a)\hat{}\delta {\varphi }_{ik}\Delta t-\Delta {\mathbf{R}}_{ik}{\mathbf{\eta }}_k^{ad}\Delta t]\\ & =\Delta {\mathbf{v}}_{ij}-\delta {\mathbf{v}}_{ij}\end{array}\text{\hspace{1em}(16)}$$
式中:
$$\Delta {\mathbf{v}}_{ij}=\sum _{k=i}^{j-1}\Delta {\mathbf{R}}_{ik}({\mathbf{a}}_k-{\mathbf{b}}_i^a)\Delta t$$
于是可得速度测量模型:
$$\Delta {\mathbf{v}}_{ij}={\mathbf{R}}_i^T({\mathbf{v}}_j-{\mathbf{v}}_i-\mathbf{g}\Delta t_{ij})+\delta {\mathbf{v}}_{ij}\text{\hspace{1em}(17)}$$

3.1.3 位置测量模型

将公式(14)(16)的结果带入公式(13)的$\Delta {\mathbf{p}}_{ij}$中，可得:
$$\begin{array}{rl}\Delta {\mathbf{p}}_{ij}& ={\mathbf{R}}_i^T({\mathbf{p}}_j-{\mathbf{p}}_i-\frac{1}{2}\mathbf{g}\Delta t_{ij}^2)\\ & =\sum _{k=i}^{j-1}[{\mathbf{v}}_{ik}\Delta t+\frac{1}{2}{\mathbf{R}}_{ik}({\mathbf{a}}_k-{\mathbf{b}}_k^a-{\mathbf{\eta }}_k^{ad})\Delta t^2]\\ & \stackrel{2,14,16}{\simeq }\sum _{k=i}^{j-1}[(\Delta {\mathbf{v}}_{ik}-\delta {\mathbf{v}}_{ik})\Delta t+\frac{1}{2}\Delta {\mathbf{R}}_{ik}(\mathbf{I}-\delta {\varphi }_{ik}\hat{})({\mathbf{a}}_k-{\mathbf{b}}_i^a)\Delta t^2-\frac{1}{2}\Delta {\mathbf{R}}_{ik}{\mathbf{\eta }}_k^{ad}\Delta t^2]\\ & =\Delta {\mathbf{p}}_{ij}+\sum _{k=i}^{j-1}[-\delta {\mathbf{v}}_{ik}\Delta t+\frac{1}{2}\Delta {\mathbf{R}}_{ik}({\mathbf{a}}_k-{\mathbf{b}}_i^a)\hat{}\delta {\varphi }_{ik}\Delta t^2-\frac{1}{2}\Delta {\mathbf{R}}_{ik}{\mathbf{\eta }}_k^{ad}\Delta t^2]]\\ & =\Delta {\mathbf{p}}_{ij}-\delta {\mathbf{p}}_{ij}\end{array}\text{\hspace{1em}(18)}$$
于是可得位置测量模型:
$$\Delta {\mathbf{p}}_{ij}={\mathbf{R}}_i^T({\mathbf{p}}_j-{\mathbf{p}}_i-\frac{1}{2}\mathbf{g}\Delta t_{ij}^2)+\delta {\mathbf{p}}_{ij}\text{\hspace{1em}(19)}$$

3.2 噪声传递

由公式(14)可知预积分姿态噪声项为:

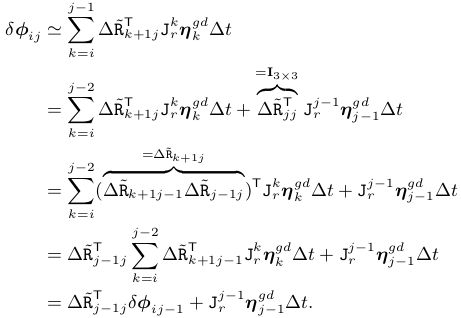
由公式(16)可知预积分速度噪声项为:

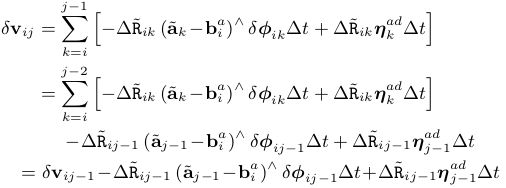
由公式(18)可知预积分位置噪声项为:

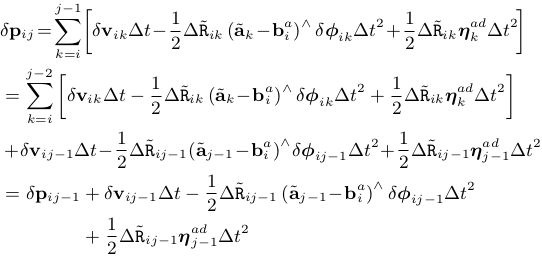
令$\Delta {\mathbf{x}}_{ik}=[\delta {\varphi }_{ik},\delta {\mathbf{v}}_{ik},\delta {\mathbf{p}}_{ik}]$，${\mathbf{\eta }}_k^d=[{\mathbf{\eta }}_k^{gd},{\mathbf{\eta }}_k^{ad}]$，于是上述三个公式可写为:
$$\begin{array}{r}\Delta {\mathbf{x}}_{ij}=\left[\begin{array}{ccc}\Delta {\mathbf{R}}_{j-1,j}^T& 0& 0\\ -\Delta {\mathbf{R}}_{i,j-1}^T({\mathbf{a}}_{j-1}-{\mathbf{b}}_i^a)\hat{}\Delta t& I& 0\\ -\frac{1}{2}\Delta {\mathbf{R}}_{i,j-1}^T({\mathbf{a}}_{j-1}-{\mathbf{b}}_i^a)\hat{}\Delta t^2& \Delta t& I\end{array}\right]\Delta {\mathbf{x}}_{i,j-1}+\left[\begin{array}{cc}{\mathbf{J}}_r^{j-1}& 0\\ 0& \Delta {\mathbf{R}}_{i,j-1}\Delta t\\ 0& \frac{1}{2}\Delta {\mathbf{R}}_{i,j-1}\Delta t^2\end{array}\right]{\mathbf{\eta }}_{j-1}^d\end{array}=A_{j-1}\Delta {\mathbf{x}}_{i,j-1}+B_{j-1}{\mathbf{\eta }}_{j-1}^d\text{\hspace{1em}(20)}$$
从上述推导可以看出，预积分噪声项的传递是线性的，因此可以直接通过如下线性传递的方式进行协方差的更新:
$$\sum _{ij}=A_{j-1}\sum _{i,j-1}{A}_{j-1}^T+B_{j-1}\sum _{\eta }{B}_{j-1}^T\text{\hspace{1em}(21)}$$

----------------------------------- 公式已敲吐血 ，后面内容后续再补 --------------------------------

3.3 偏置更新

3.4 IMU预积分因子

3.5 IMU偏置模型

4. 代码解析

参考

On-Manifold Preintegration for Real-Time Visual-Inertial Odometry
《视觉SLAM十四讲》
https://blog.csdn.net/l741299292/article/details/81203464
IMU预积分总结与公式推导三