线性表的链式存储结构-单链表及循环链表
目录
- 1. 链式存储定义
- 2. 单链表
-
- 2.1 单链表初始化
- 2.2 单链表插入数据
- 2.3 单链表删除数据
- 2.4 单链表读取数据
- 2.5 头插法整体创建链表
- 2.6 尾插法整体创建链表
- 2.7 单链表整体删除
- 3. 单链表与顺序存储结构优缺点
- 4. 循环链表
-
- 4.1 循环链表定义
- 4.2 循环链表创建
- 4.3 循环链表插入数据
- 4.4 循环链表删除数据
- 4.5 循环链表查询数据位置
1. 链式存储定义
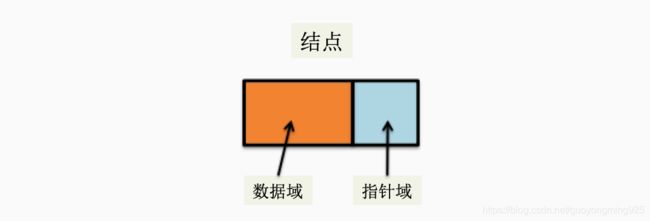
为了表示每个数据元素ai与其直接后继数据元素ai+1之间的逻辑关系,对数据元素ai来说,除了存储其本身的信息之外,还需存储一个指示其直接后继的信息。我们把存储数据元素信息的域称为数据域,把存储直接后继位置的域称为指针域。这两部分信息组成数据元素的存储映像,称为结点。
n个结点链组成一个链表,即为线性表的链式存储结构,因为此链表的每个结点中只包含一个指针域,所以叫做单链表。
对于线性表来说,有头有尾,链表中的第一个结点的存储位置叫做头指针,链表的存取必须是从头指针开始进行。
有时候我了增加对链表操作的方便性,我们会在链表的第一个结点(首元结点)前增加一个结点,称为头结点。头结点的数据域可以不存任何数据,指针域存储第一个结点的指针。
链式存储结构中我们默认都带上头结点。
图片示意如下:
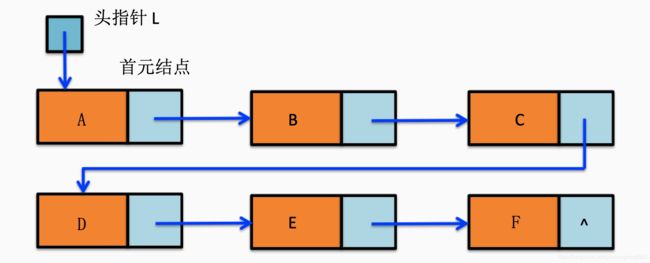
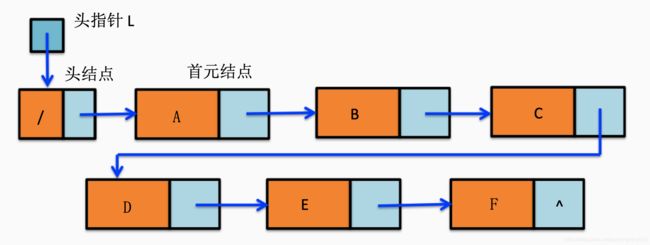
头指针和头结点的区别:
头指针:
- 头指针是指链表指向第一个结点的指针,若链表有头结点,则是指向头结点的指针。
- 头指针具有标识作用,所以常用头指针冠以链表的名字。
- 无论链表是否为空,头指针均不为空。头指针是链表的必要元素。
头结点:
- 头结点是为了操作的统一和方便而设立的,放在第一个元素的结点前,其数据域一般无意思。
- 有了头结点,对在第一个元素结点前插入结点和删除第一个结点,与操作其他结点的操作就统一了。
- 头结点不一定是链表的必要元素。
2. 单链表
结点定义如下:
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
/* ElemType类型根据实际情况而定,这里假设为int */
typedef int ElemType;
/* Status是函数的类型,其值是函数结果状态代码,如OK等 */
typedef int Status;
//定义结点
typedef struct Node{
ElemType data; // 存储在数据域中的数据
struct Node *next; // 直接后继结点的地址指针
}Node;
typedef struct Node * LinkList;
2.1 单链表初始化
思路:
- 在内存开辟空间,创建头结点。
- 初始化头结点。
Status InitList(LinkList *L){
//产生头结点,并使用L指向此头结点
*L = (LinkList)malloc(sizeof(Node));
//存储空间分配失败
if(*L == NULL) return ERROR;
//将头结点的指针域置空
(*L)->next = NULL;
return OK;
}
2.2 单链表插入数据
假设要在单链表的两个数据元素A和B之间插⼊一个数据元素e,已知p为其单链表存储结构中指向结点A指针。如下图所示

思路:
- 声明一结点p指针指向链表头结点,初始化j从1开始。
- 当j
- 若到链表末尾p为空,则说明插入的位置不存在。
- 否则查找成功,在系统中生成一个空节点s。
- 将数据元素e赋值给s->data。
- 然后将s->next指向p->next,p->next指向s。
- 返回成功。
代码实现如下:
/*
初始条件:顺序线性表L已存在,1≤i≤ListLength(L);
操作结果:在L中第i个位置之前插入新的数据元素e,L的长度加1;
*/
Status ListInsert(LinkList *L,int i,ElemType e){
int j;
LinkList p,s;
p = *L;
j = 1;
//寻找第i-1个结点
while (p && j<i) {
p = p->next;
++j;
}
//第i-1个元素不存在
if(!p || j>i) return ERROR;
//生成新结点s
s = (LinkList)malloc(sizeof(Node));
//将e赋值给s的数值域
s->data = e;
//将p的后继结点赋值给s的后继
s->next = p->next;
//将s赋值给p的后继
p->next = s;
return OK;
}
2.3 单链表删除数据
要删除单链表中指定位置的元素,同插入元素一样,首先应该找到该位置的前驱结点,如下图所示在单链表中删除元素B时,应该首先找到其前驱结点A,为了在单链表中实现元素A,B,C之间的逻辑关系的变化,仅需修改结点A中的指针域即可.
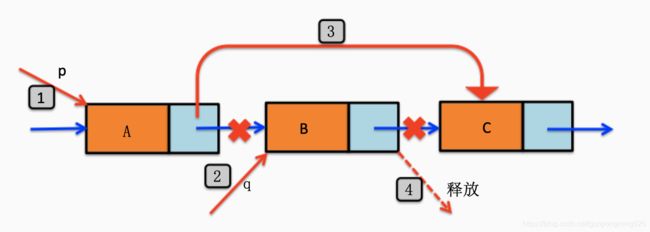
思路:
- 声明一结点p指针指向链表头结点,初始化j从1开始。
- 当j
- 若到链表末尾p为空,则说明删除的位置不存在。
- 否则查找成功,则将q指向要删除的结点。
- 将q的直接后继赋值给p的直接后继。
- 将q结点中的数据给e。
- 释放删除的结点。
- 返回成功。
代码实现如下:
/*
初始条件:顺序线性表L已存在,1≤i≤ListLength(L)
操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减1
*/
Status ListDelete(LinkList *L,int i,ElemType *e){
int j;
LinkList p,q;
p = *L;
j = 1;
//查找第i-1个结点,p指向该结点
while (p->next && j<i) {
p = p->next;
++j;
}
//当i>n 或者 i<1 时,删除位置不合理
if (!(p->next) || j>i) return ERROR;
//q指向要删除的结点
q = p->next;
//将q的后继赋值给p的后继
p->next = q->next;
//将q结点中的数据给e
*e = q->data;
//让系统回收此结点,释放内存;
free(q);
return OK;
}
2.4 单链表读取数据
在单链表中,我们不能像顺序存储结构那样直接通过下标直接获取数据,我们没办法一开始就知道,必须得从头开始找,进行遍历。
思路:
- 声明一结点p指针指向链表首元结点(不是头结点),初始化j从1开始。
- 当j
- 若到链表末尾p为空,则说明读取的元素不存在。
- 否则查找成功,返回节点p的数据。
代码实现如下:
/*
初始条件: 顺序线性表L已存在,1≤i≤ListLength(L);
操作结果:用e返回L中第i个数据元素的值
*/
Status GetElem(LinkList L,int i,ElemType *e){
int j = 1;
//声明结点p;
LinkList p;
//将结点p 指向链表L的首元结点;
p = L->next;
//p不为空,且计算j不等于i,则循环继续
while (p && j<i) {
//p指向下一个结点
p = p->next;
++j;
}
//如果p为空或者j>i,则返回error
if(!p || j > i) return ERROR;
//e = p所指的结点的data
*e = p->data;
return OK;
}
2.5 头插法整体创建链表
思路:
- 声明一个结点p。
- 初始化一空链表L。
- 让L的头结点的指针指向NULL,即建立一个带头结点的单链表。
- 循环:
①. 生成一个新的结点赋值给p。
②. 给p->data赋值。
③.将p插入到头结点之后。
代码实现如下:
/* 随机产生n个元素值,建立带表头结点的单链线性表L(前插法)*/
void CreateListHead(LinkList *L, int n){
LinkList p;
//建立1个带头结点的单链表
*L = (LinkList)malloc(sizeof(Node));
(*L)->next = NULL;
//循环前插入随机数据
for(int i = 0; i < n;i++)
{
//生成新结点
p = (LinkList)malloc(sizeof(Node));
//i赋值给新结点的data
p->data = i;
p->next = (*L)->next;
//将结点P插入到头结点之后;
(*L)->next = p;
}
}
2.6 尾插法整体创建链表
思路:
- 声明一个结点p、r, r指向尾部结点。
- 初始化一空链表L。
- 让L的头结点的指针指向NULL,即建立一个带头结点的单链表。
- 循环:
①.生成一个新的结点赋值给p。
②.给p->data赋值。
③.将p插入到尾部结点r之后。 - 将尾结点r的next设置为NULL。
代码实现如下:
/* 随机产生n个元素值,建立带表头结点的单链线性表L(后插法)*/
void CreateListTail(LinkList *L, int n){
LinkList p,r;
//建立1个带头结点的单链表
*L = (LinkList)malloc(sizeof(Node));
//r指向尾部的结点
r = *L;
for (int i=0; i<n; i++) {
//生成新结点
p = (Node *)malloc(sizeof(Node));
p->data = i;
//将表尾终端结点的指针指向新结点
r->next = p;
//将当前的新结点定义为表尾终端结点
r = p;
}
//将尾指针的next = null
r->next = NULL;
}
2.7 单链表整体删除
思路:
- 声明一个结点p和q。
- 将第一个结点赋值给p。
- 循环:
①. 将下一个结点赋值给q。
②. 释放p。
③. 将q赋值给p。 - 将头结点的next设置为NULL。
代码实现如下:
/* 初始条件:顺序线性表L已存在。操作结果:将L重置为空表 */
Status ClearList(LinkList *L)
{
LinkList p,q;
p=(*L)->next; /* p指向第一个结点 */
while(p) /* 没到表尾 */
{
q=p->next;
free(p);
p=q;
}
(*L)->next=NULL; /* 头结点指针域为空 */
return OK;
}
3. 单链表与顺序存储结构优缺点
存储分配方式:
- 顺序存储结构用一段连续的存储单元依次存储线性表的数据元素。
- 单链表采用链式存储结构,用一组任意的存储单元存放线性表的元素。
时间性能:
- 查找
- 顺序存储结构O(1)。
- 单链表O(n)。
- 插入与删除
- 顺序存储结构需要平均移动表长一半的元素,时间为O(n)。
- 单链表在找出某位置的指针后,插入和删除时间为O(1)。
空间性能:
- 顺序存储结构需要预分配存储空间,分大了,浪费,分小了,容易溢出。
- 单链表不需要分配存储空间,只要有就可以分配,元素个数也不受限制。
通过对比,我们可得知:
若线性表需要频繁查找,很少进行插入和删除操作时,宜采用顺序存储结构。若需要频繁插入和删除时,宜采用单链表结构。
当线性表中的元素个数变化较大或者根本不知道有多大的时候,最好采用单链表结构,这样可以不需要考虑存储空间大小的问题。而如果事先知道线性表的大致长度,就可以用这个顺序存储结构,用起来比较高效。
4. 循环链表
4.1 循环链表定义
将单链表中的终端结点的指针从空指针改为指向头结点,就使整个单链表形成一个环,这种头尾相接的单链表称为单循环链表,简称循环链表。
为了使空链表与非空链表处理一致,我们通常设一个头结点。
循环列表中带有头结点的空链表如下图:
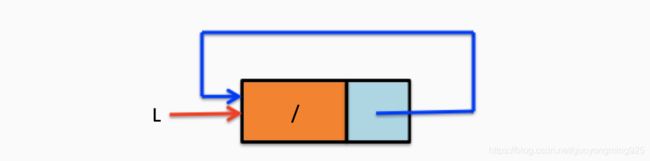
对于非空的循环链表如下图:
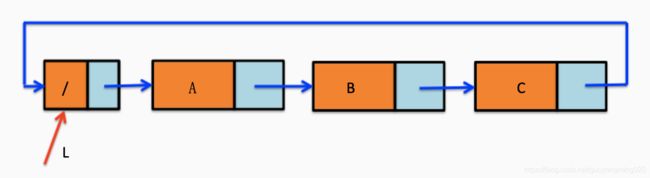
4.2 循环链表创建
思路:
- 判断链表是否已经存在,即是否已经存在头结点。
- 如果存在头结点,那么直接依次往里插入数据。
- 如果不存在头结点,那么先创建头结点,然后依次往里插入数据。
- 返回OK。
代码实现:
/* 创建一个带有头结点的循环链表 */
Status CreateList(LinkList *L) {
int item;
LinkList temp = NULL;
LinkList r = NULL; // 尾结点指针
printf("请输入新的结点, 当输入0时结束!\n");
while (1) {
scanf("%d",&item);
if (item == 0) {
break;
}
// 当链表为空时,创建链表,带上头结点。
if (*L == NULL) {
*L = (LinkList)malloc(sizeof(Node));
if (!*L) return ERROR;
(*L)->next = *L; // 使其next指针指向自己
r = *L;
}
temp = (LinkList)malloc(sizeof(Node));
if(!temp) return ERROR;
temp->data = item;
temp->next = *L;
r->next = temp;
r = temp;
}
return OK;
}
4.3 循环链表插入数据
思路:
- 创建新结点temp,并判断是否创建成功,成功则赋值,否则返回ERROR。
- 先找到插入的位置的前一个结点target,如果插入位置超过链表长度,则自动插入队尾。
- 新结点的next指向target原来的next位置,target的next指向新结点。
- 返回OK。
代码实现如下:
/* 循环链表插入数据 */
Status ListInsert2(LinkList *L, int place, int num) {
if (place < 1) {
return ERROR;
}
LinkList target;
LinkList temp;
int k;
temp = (LinkList)malloc(sizeof(Node));
if (!temp) return ERROR;
temp->data = num;
// 查找插入位置的前一个结点
for (k = 1, target = *L; k < place && target->next != *L; k++, target = target->next);
temp->next = target->next;
target->next = temp;
return OK;
}
4.4 循环链表删除数据
思路:
- 创建新结点temp,用于记录要删除的元素。
- 先找到删除位置的前一个结点target,如果删除的位置大于链表长度,返回ERROR。
- 将target->next赋值给temp,temp->next赋值给target->next。
- 释放temp。
- 返回OK。
代码实现如下:
/* 循环链表删除数据,链表表L已存在,1≤place≤ListLength(L) */
Status LinkListDelete(LinkList *L,int place) {
if (place < 1) {
return ERROR;
}
LinkList temp, target;
int k;
for (k = 1, target = *L; k < place && target->next != *L; k++, target = target->next);
if (place > k) {
return ERROR;
}
temp = target->next;
target->next = temp->next;
free(temp);
return OK;
}
4.5 循环链表查询数据位置
思路:
- 创建结点指针p,并将p指向首元结点,声明变量i,用来记录位置。
- 循环查找结点值等于value的结点,直到遍历到最后一个节点停止。
- 如果已经遍历到最后一个元素,且还没有找到,那么直接返回-1.
- 返回查找到的位置。
代码实现如下:
/* 循环链表查询值的位置 */
int findValue(LinkList L, int value) {
int i = 1;
LinkList p;
p = L->next;
while (p->data != value && p->next != L) {
i++;
p = p->next;
}
// 如果已经遍历到最后一个元素,且还没有找到,那么直接返回-1.
if (p->next == L && p->data != value) {
return -1;
}
return i;
}