LeetCode48. 旋转图像

描述

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

实例

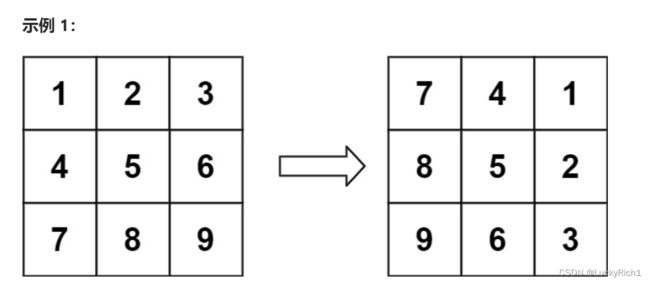
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

解题思路1

这道题大多数人的解题思路就是申请一个同样大小的辅助vector，将翻转90°的结果保存到这个辅助vector里，然后再将结果拷贝到matrix中，这样就可以得到正确结果。

具体代码如下

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n=matrix.size();
        auto result=matrix;
        for(int i=0;i<n;++i)
        {
            for(int j=0;j<n;++j)
            {
                result[j][n-i-1]=matrix[i][j];
            }
        }
        //拷贝
        matrix=result;
    }
};

这道题虽然成功解决了，但是效率并不理想。
时间复杂度：O(N^2)。
空间复杂度O(N^2)。

因此根据上面思路1发展到思路2。

解题思路2

原地旋转图像。

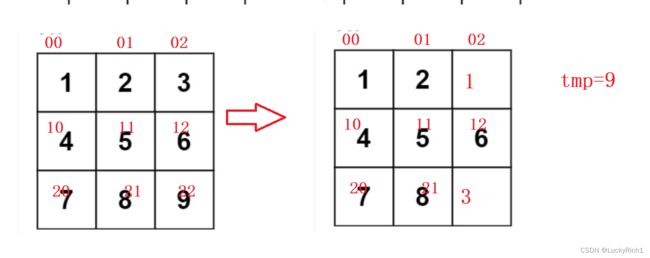
下标00旋转到02位置，但是会把下标02的数字覆盖，因此需要一个临时变量保存02位置，

tmp=matrix[i][n-j-1];
matrix[i][n-j-1]=matrix[i][j];

这时如果我再旋转下标01到下标12可以吗？显示不可以，因为tmp保存的变量，我还没有放置，再还没有放置tmp情况下，再给tmp赋值，就找不到原来的值了。因此需要先把tmp给处理掉。
这里解决方法，按照顺时针边界旋转放置

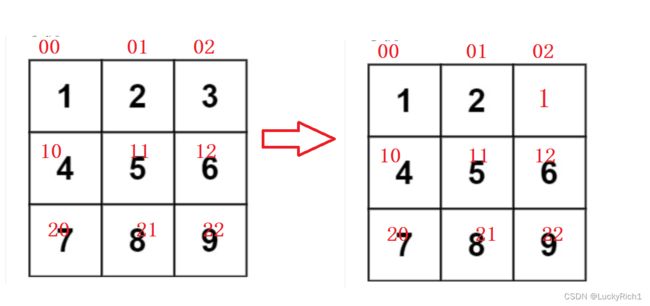
把01放到02之前，先把02放到22，

tmp=matrix[n-i-1][n-j-1];
matrix[n-j-1][n-i-1]=matrix[j][n-i-1];
matrix[j][n-i-1]=matrix[i][j];

放下一个下标之前，还需要把9先放，9放在7的位置，因此tmp最先保持的应该是7；

tmp=matrix[n-j-1][i];
matrix[n-j-1][i]=matrix[n-j-1][n-i-1];
matrix[n-j-1][n-i-1]=matrix[j][n-i-1];
matrix[j][n-i-1]=matrix[i][j]

再放下一个下标，需要把7先放置，这样看起来一个顺时针边界旋转，因此tmp首先保存1，然后放7，放9，放3，最后放1。这样就完成了一次循环，最后控制边界就好了。

tmp=matrix[i][j];
matrix[i][j]=matrix[n-j-1][i];
matrix[n-j-1][i]=matrix[n-i-1][n-j-1];
matrix[n-i-1][n-j-1]=matrix[j][n-i-1];
matrix[j][n-i-1]=tmp;

最终代码如下

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n=matrix.size();
        for(int i=0;i<n/2;++i)
        {
            for(int j=i;j<n-i-1;++j)
            {
                int tmp=matrix[i][j];
                matrix[i][j]=matrix[n-j-1][i];
                matrix[n-j-1][i]=matrix[n-i-1][n-j-1];
                matrix[n-i-1][n-j-1]=matrix[j][n-i-1];
                matrix[j][n-i-1]=tmp;
            }
        }
    
    }
};