合成孔径雷达成像–算法与实现 读书笔记(1-2章)
注:仅作为学习笔记,如有错漏,还请各位大佬指出
文章目录
- 第1章 概论
-
- 第2章 信号处理基础
-
- 2.1 线性卷积
-
- 2.3 傅里叶变换
-
- 2.3.1连续时间傅里叶变换
- 2.3.2 离散傅里叶变换
- 2.3.3 傅里叶变换的性质
- 2.4 卷积的DFT计算
- 2.5 信号采样
-
- 2.6 平滑窗
- 2.7 插值
- 2.8 点目标分析
第1章 概论
1.2 遥感中的雷达
SAR在遥感领域获得越来越多的应用,主要基于以下三个原理:
- 雷达自带照射源,在黑夜中同样能出色地工作。
- 一般雷达所使用波段的电磁波几乎可以无失真地穿透水汽云层。
- .物质的光学散射能量与其雷达电磁散射能量是不同的,因此雷达与光学传感器具有互补性,有时甚至比光学传感器具有更强的地表特征区分能力。
1.3 SAR基础
在遥感中, SAR借助机载或星载平台获得地表图像。这一过程是通过雷达波束沿着与传感器运动矢量近乎垂直的方向发射相位调制(phase-encoded)脉冲,接收并记录经地表反射后的回波来完成的。
为了获得地面图像,需要在两个相互正交的的轴向上进行强度测量:
距离向(x轴):近似平行于波束指向;
方位向(y轴):沿轨迹方向。
SAR的几种工作模式:
根据不同的工作模式,合成孔径雷达分为:条带式合成孔径雷达、扫描式合成孔径雷达、聚束合成孔径雷达、逆合成孔径雷达、双站合成孔径雷达和干涉合成孔径雷达。
SAR分辨率
1.利用多普勒频移合成大孔径,提高分辨率;
2.方位向分辨率等于天线尺寸的二分之一,与距离无关。
距离徙动
由于合成孔径内传感器的移动,雷达与目标的距离随时间变化,这种距离的变化导致距离徙动。如下图所示:

图1 距离徙动
第2章 信号处理基础
2.1 线性卷积
2.1.1连续时间卷积
在连续时域,信号s(t)和滤波器h(t)的卷积:
y ( t ) = s ( t ) ⊗ h ( t ) = ∫ − ∞ ∞ s ( u ) h ( t − u ) d u = ∫ − ∞ ∞ s ( t − u ) h ( u ) d u y(t)=s(t) \otimes h(t) =\int_{-\infty}^{\infty} s(u) h(t-u) d u =\int_{-\infty}^{\infty} s(t-u) h(u) d u y(t)=s(t)⊗h(t)=∫−∞∞s(u)h(t−u)du=∫−∞∞s(t−u)h(u)du
从几何角度对卷积进行理解:
1.反褶:生成h(u)的时间反褶图像h(-u),其中u是虚时间。
2.移位:将h(-u)以一定的时间位移t滑过信号。
3.重合部分乘积:在每一位移点上,对h(t - u)和信号s(u)的重叠乘积进行积分,这种积分又称为“内积”。
注意,信号s(t),y(t)和滤波器h(t)也可以是复数。
相关的定义·:
Φ s h ( t ) = ∫ − ∞ ∞ s ( u ) h ∗ ( u − t ) d u \Phi_{\mathrm{sh}}(t)=\int_{-\infty}^{\infty} s(u) h^{*}(u-t) d u Φsh(t)=∫−∞∞s(u)h∗(u−t)du
其中h*表示复变量h的复共辄。在几何上,相关又解释为滑动内积。
区别:与卷积不同,相关不需要进行反转;如果滤波器是复的,则还需取共辄。通常,相关是对等式右边的两个信号进行比较,其中t为时间延迟。与卷积不同,相关是不可交换的,但是
Φ s h ( t ) = Φ s h ∗ ( − t ) \Phi_{\mathrm{sh}}(t)=\Phi_{\mathrm{sh}}^{*}(-t) Φsh(t)=Φsh∗(−t)
二维卷积
定义:
y ( t 1 , t 2 ) = s ( t 1 , t 2 ) ⊗ h ( t 1 , t 2 ) = ∫ − ∞ ∞ ∫ − ∞ ∞ s ( u 1 , u 2 ) h ( t 1 − u 1 , t 2 − u 2 ) d u 1 d u 2 = ∫ − ∞ ∞ ∫ − ∞ ∞ s ( t 1 − u 1 , t 2 − u 2 ) h ( u 1 , u 2 ) d u 1 d u 2 \begin{aligned} y\left(t_{1}, t_{2}\right) &=s\left(t_{1}, t_{2}\right) \otimes h\left(t_{1}, t_{2}\right) \\ &=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} s\left(u_{1}, u_{2}\right) h\left(t_{1}-u_{1}, t_{2}-u_{2}\right) d u_{1} d u_{2} \\ &=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} s\left(t_{1}-u_{1}, t_{2}-u_{2}\right) h\left(u_{1}, u_{2}\right) d u_{1} d u_{2} \end{aligned} y(t1,t2)=s(t1,t2)⊗h(t1,t2)=∫−∞∞∫−∞∞s(u1,u2)h(t1−u1,t2−u2)du1du2=∫−∞∞∫−∞∞s(t1−u1,t2−u2)h(u1,u2)du1du2
SAR信号是二维信号,其滤波可用二维卷积处理,缺点是二维卷积计算量非常大,一般对二维滤波器解耦为两个一维滤波器。
h ( t 1 , t 2 ) = h 1 ( t 1 ) ⊗ h 2 ( t 2 ) h\left(t_{1}, t_{2}\right)=h_{1}\left(t_{1}\right) \otimes h_{2}\left(t_{2}\right) h(t1,t2)=h1(t1)⊗h2(t2)
根据卷积结合律,滤波常用的二维卷积计算方式如下:
y ( t 1 , t 2 ) = s ( t 1 , t 2 ) ⊗ [ h 1 ( t 1 ) ⊗ h 2 ( t 2 ) ] = [ s ( t 1 , t 2 ) ⊗ h 1 ( t 1 ) ] ⊗ h 2 ( t 2 ) \begin{aligned} y\left(t_{1}, t_{2}\right) &=s\left(t_{1}, t_{2}\right) \otimes\left[h_{1}\left(t_{1}\right) \otimes h_{2}\left(t_{2}\right)\right] \\ &=\left[s\left(t_{1}, t_{2}\right) \otimes h_{1}\left(t_{1}\right)\right] \otimes h_{2}\left(t_{2}\right) \end{aligned} y(t1,t2)=s(t1,t2)⊗[h1(t1)⊗h2(t2)]=[s(t1,t2)⊗h1(t1)]⊗h2(t2)
2.2.2 离散时间卷积
对于离散信号s(n)和滤波器h(n),对它们进行离散时间卷积,其运算过程如下图所示:<>
图2 离散时间卷积运算
从上图可以看出,对于信号长度为K,滤波器长度为M的离散卷积,其输出y(n)的长度为K+M -1,但是上图中在n=0和1及n=8和9上,信号仅与滤波器系数的子集相乘,输出结果为部分卷积的。
二维卷积
对于滤波器h维数为M1*M2的二维卷积
y ( n 1 , n 2 ) = s ( m 1 , m 2 ) ⊗ h ( n 1 , n 2 ) = ∑ m 1 = 0 M 1 ∑ m 2 = 0 M 2 s ( n 1 − m 1 , n 2 − m 2 ) h ( m 1 , m 2 ) = ∑ m 1 = n 1 − ( M 1 − 1 ) n 1 ∑ m 2 = n 2 − ( M 2 − 1 ) n 2 s ( m 1 , m 2 ) h ( n 1 − m 1 , n 2 − m 2 ) \begin{aligned} y\left(n_{1}, n_{2}\right) &=s\left(m_{1}, m_{2}\right) \otimes h\left(n_{1}, n_{2}\right) \\ &=\sum_{m_{1}=0}^{M_{1}} \sum_{m_{2}=0}^{M_{2}} s\left(n_{1}-m_{1}, n_{2}-m_{2}\right) h\left(m_{1}, m_{2}\right) \\ &=\sum_{m_{1}=n_{1}-\left(M_{1}-1\right)}^{n_{1}} \sum_{m_{2}=n_{2}-\left(M_{2}-1\right)}^{n_{2}} s\left(m_{1}, m_{2}\right) h\left(n_{1}-m_{1}, n_{2}-m_{2}\right) \end{aligned} y(n1,n2)=s(m1,m2)⊗h(n1,n2)=m1=0∑M1m2=0∑M2s(n1−m1,n2−m2)h(m1,m2)=m1=n1−(M1−1)∑n1m2=n2−(M2−1)∑n2s(m1,m2)h(n1−m1,n2−m2)
二维卷积滤波器可以解耦为
h ( n 1 , n 2 ) = h 1 ( n 1 ) ⊗ h 2 ( n 2 ) h\left(n_{1}, n_{2}\right)=h_{1}\left(n_{1}\right) \otimes h_{2}\left(n_{2}\right) h(n1,n2)=h1(n1)⊗h2(n2)
第一种方法在MATLAB上实现方式为:conv2(h,s)
第二种方法在MATLAB上实现方式为:conv2(h1,h2,s)
上述分解在显著减少算术运算的同时还节省了存储空间。使用h(ny, nz),计算一个输出点要进行2M1M2-1次运算(M1M2次相乘和M1M2- 1次相加),而使用式h1(n)和h2(n,)仅需进行2(M1+M2-1)次运算。
2.3 傅里叶变换
2.3.1连续时间傅里叶变换
2.3.2 离散傅里叶变换
2.3.3 傅里叶变换的性质
补零:在离散时间下,某一域(频域或时域)中的序列补零相当于对另一域进行升采样。这使得另一域中的数据量增大,但不会改变序列的信息内容(例如带宽)。
二维扭曲和旋转:在某一域中沿某一数据轴进行的扭曲,会导致另一域中沿另一轴的数据扭曲:
g ( t 1 − α t 2 , t 2 ) ⟷ G ( f 1 , f 2 + α f 1 ) g\left(t_{1}-\alpha t_{2}, t_{2}\right) \longleftrightarrow G\left(f_{1}, f_{2}+\alpha f_{1}\right) g(t1−αt2,t2)⟷G(f1,f2+αf1)
g ( t 1 , t 2 − α t 1 ) ⟷ G ( f 1 + α f 2 , f 2 ) g\left(t_{1}, t_{2}-\alpha t_{1}\right) \longleftrightarrow G\left(f_{1}+\alpha f_{2}, f_{2}\right) g(t1,t2−αt1)⟷G(f1+αf2,f2)
某一域中的角度旋转将导致另一域中同样的角度旋转:
g ( t 1 ′ , t 2 ′ ) ⟷ G ( f 1 ′ , f 2 ′ ) g\left(t_{1}^{\prime}, t_{2}^{\prime}\right) \longleftrightarrow G\left(f_{1}^{\prime}, f_{2}^{\prime}\right) g(t1′,t2′)⟷G(f1′,f2′)
由以上两式可知:图像的垂直扭曲会导致频谱的水平扭曲,图像旋转则导致频谱相同的旋转。MATLAB中使用fftshift使峰值出现在图像中心。
2.4 卷积的DFT计算
由于DFT和IDFT的周期假设和循环寻址,卷积实际上是周期卷积或循环卷积。通过将序列补零至合适的长度,就可以利用DFT进行线性卷积.卷积的循环性质如下图所示:
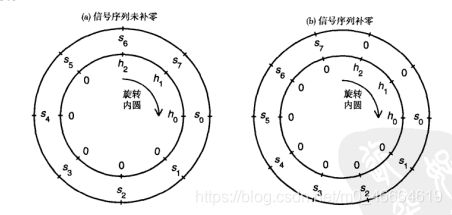
图3 使用DFT时卷积的循环特性
注意区分有效点、弃置点以及部分卷积点
2.5 信号采样
对时域信号采样,一般只考虑有限长度的信号;当对采样信号进行N点DFT时,输出序列第一个样本的频率为零,最后一个样本的频率为(N - 1)f,/N ~f,。通常将DFT输出序列的左右两半互相交换。这种操作在MATLAB中是通过fftshift完成的。互换后,序列第一个样本频率为-fs/2,最后一个样本频率为(N 一2)f,/2N 一f,/2。对于实信号,DFT输出序列的前一半就可以完整地描述信号,后一半则是冗余的。
2.5.1 奈奎斯特采样率和混叠
实信号采样:对于有限带宽的连续基带实信号,采样率必须高于最高信号频率的两倍
非基带实信号(带通信号):采样率必须高于非基带实信号带宽的两倍
复信号采样:复信号的奈奎斯特采样率与信号带宽相等
2.6 平滑窗
在脉冲压缩中使用窗来控制旁瓣,同时保持高的分辨率。通常使用凯kaiser窗,该窗可以均衡旁瓣和分辨率。在MATLAB中命令为:Kaiser(N,beat)
2.7 插值
插值可以实现样本的位置移动,通过DFT的平移/调制或频谱的补零实现插值,前者仅能得到一定偏移后的初始信号采样点,而后者仅能得到间隔为1/M的采样点,其中M是扩展系数(必须为整数)
下面通过卷积来实现插值:
g ( x ) = ∑ i g d ( i ) h ( x − i ) g(x)=\sum_{i} g_{d}(i) h(x-i) g(x)=∑igd(i)h(x−i)
h(x)称为插值因子或插值核。在实际应用时,核是x的偶函数,故h(x - i)= h(i -x)。i处的样本被核(i-x)加权。插值点x处的g(x)等于插值核内的样本 g d ( i ) g_{d}(i) gd(i)与h(i-x)的乘积之和,即g(x)等于x邻域样本的加权和。
sinc插值
条件:1.信号是带限的,即最高频率有界;2采样满足麦奎斯特频率
重建方程
sinc核h(x),插值信号g(x)
h ( x ) = sinc ( x ) = sin ( π x ) π x g ( x ) = ∑ i g d ( i ) sinc ( x − i ) \begin{array}{l} h(x)=\operatorname{sinc}(x)=\frac{\sin (\pi x)}{\pi x} \\ g(x)=\sum_{i} g_{d}(i) \operatorname{sinc}(x-i) \end{array} h(x)=sinc(x)=πxsin(πx)g(x)=∑igd(i)sinc(x−i)
注意插值核的归一化
2.8 点目标分析
IRW:冲击响应宽度指冲击响应的3dB主瓣宽度,在SAR处理中又称为图像分辨率。
PSLR:峰值旁瓣比指最大旁瓣与主瓣的高度比,sinc函数为-13dB,比较大。
一维ISLR:
ISLR = 10 log 10 { P total − P main P main } \text { ISLR }=10 \log _{10}\left\{\frac{P_{\text {total }}-P_{\text {main }}}{P_{\text {main }}}\right\} ISLR =10log10{Pmain Ptotal −Pmain }
峰值位置:指二维样本空间中的冲击响应峰值位置。一般用于几何定标(图像的相对或绝对几何定位精度)
信号峰值幅度:指峰值点处目标响应幅度。可用于辐射定标(测量目标的雷达截面积)
相位:相位是干涉和极化等应用中的重要参数,由于压缩后目标在冲激响应峰值两侧存在斜坡,故某一方向上测量出的点目标相位特性可能与另一方向不同。


