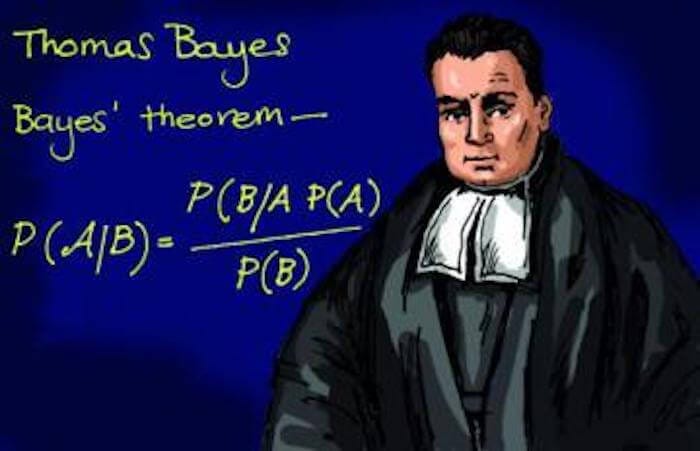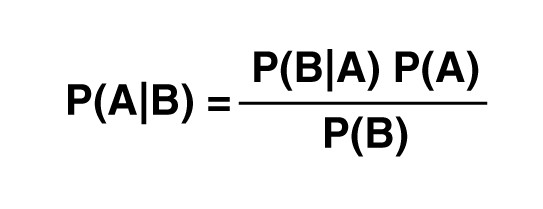【概率论教程01】对贝叶斯定理的追忆
一、说明
贝叶斯定理,是一个需要反复体悟的道理,不是说公式解释清除就算Grasp,而是需要反复在实际项目中发挥,才能算掌握了。而实际应用中,并不是简单给出条件就可以套用,而是隐藏在迷雾一样的事实中,本人认为,最难办的两个事情是:1)隐变元问题,2)连续性假设。3)分布和分布的比较。总之,用好贝叶斯理论是需要下点苦功的。
二、提要
概率分布是统计推断的支柱,要理解这些分布,我们至少应该对概率论有一些基本的了解。
2.1 这篇文章的目的是建立概率基础,我们将在本文中介绍的主题是:
- 对概率的理解
- 基本术语,如样本空间、事件、实验和结果。
- 概率公理
- 事件类型:独立事件、从属事件等
- 概率规则:加法和乘法规则。
- 条件概率的概念
- 贝叶斯定理
2.2 了解概率论
概率论涉及不确定性和随机性的研究,提供分析事件和量化其发生可能性的工具。
三、基本术语
3.1 概率
概率是事件发生的可能性。
3.2 实验和结果
实验是指生成一组可能的结果或结果的过程或活动。这是我们有兴趣从概率角度研究的基本行为。
结果是作为实验结果而发生的单个结果。 它代表了给定实验中可能发生的单个结果之一。例如,当掷出公平的六面骰子时,可能的结果是数字 1、2、3、4、5 或 6。
等可能结果:当样本空间中的所有结果都有相同的发生机会时,它们被称为等可能结果。例如,在抛出一枚公平的硬币时,结果(正面或反面)的可能性相同。
3.3 样品空间和活动:
样本空间包含实验或观察的所有可能结果。
事件是样本空间的子集,表示感兴趣的特定结果。
3.4 不同类型的事件:
- Simple Event and Compound Event: If an event consists of a single result from the sample space, it is termed a simple event. For example, in rolling a fair six-sided dice we have a sample space of 1,2,3,4,5,6, but getting a “3” is a simple event. However, if want to have a number less than 3, then the event has more than two outcomes that is 1 and 2. Such events are known as compound events.
- 详尽的活动:穷举事件是一组共同覆盖整个样本空间的事件。换句话说,这些事件的并集等于整个样本空间。例如,在掷出一个公平的六面骰子时,得到一个小于 7 和大于 0 的数字将给我们整个空间“1”、“2”、“3”、“4”、“5”或“6”。此类事件是详尽无遗的事件,因为它们涵盖了所有可能的结果。
- 互斥活动:互斥事件是不能同时发生的事件。如果两个事件是相互排斥的,则意味着它们没有共同的结果。在数学上,如果 A 和 B 是互斥事件,则它们的交集 (A ∩ B) 是一个空集 (∅)。例如,在掷硬币时,事件“正面”和“反面”是相互排斥的。
- 独立活动:如果一个事件的发生不影响另一个事件的概率,则两个事件 A 和 B 是独立的。换句话说,一个事件发生的概率不取决于另一个事件发生。在数学上,对于独立事件 A 和 B,P(A ∩ B) = P(A) * P(B)。
- 依赖事件:如果一个事件的发生影响另一个事件的概率,则两个事件 A 和 B 是相关的。在这种情况下,一个事件发生的概率取决于另一个事件发生。在数学上,对于相关事件 A 和 B,P(A ∩ B) ≠ P(A) * P(B)。
四、如何找到事件的概率?
要找到概率中事件发生的可能性,步骤如下:
- 确定样本空间或实验可能结果的总数。
- 确定事件的有利结果的数量。
- 将步骤 2 中的值除以步骤 1 中获得的值以获得所需的概率。
4.1 概率公理
- 非负性:任何事件的概率都是非负值。也就是说,对于任何事件 A,P(A) ≥ 0。
- 规范化:事件的概率是介于 0 和 1 之间的数字,其中 0 表示不可能,1 表示确定性,介于两者之间的值表示发生的可能性。
- 加法:对于任何互斥事件(不能同时发生的事件),它们的并集概率等于它们各自概率的总和。也就是说,对于互斥事件 A 和 B,其中 A ∩ B = ∅(空集),P(A ∪ B) = P(A) + P(B)。
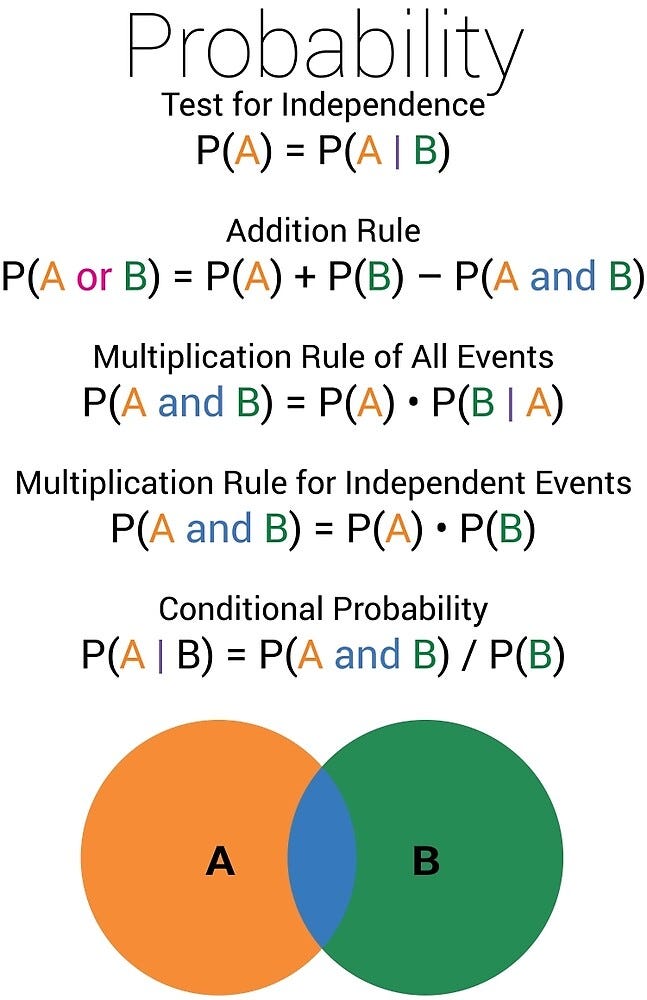
4.2 概率规则
加法规则和乘法规则是概率论中的基本原理,有助于计算复合事件的概率。
4.3.1 乘法规则
乘法规则指出,两个独立事件(A ∩ B)相交的概率等于它们各自概率的乘积:
P(A ∩ B) = P(A) * P(B)
如果有两个以上的独立事件,则规则将扩展到:
P(A ∩ B ∩ C ∩ ...) = P(A) * P(B) * P(C) * ...
4.3.2 加法规则
加法规则指出,两个互斥事件(A ∪ B)并集的概率等于它们各自概率的总和:
P(A ∪ B) = P(A) + P(B)
如果有两个以上的互斥事件,则规则将扩展到:
P(A ∪ B ∪ C ∪ ...) = P(A) + P(B) + P(C) + ...
4.3.3 补充规则
每当一个事件是另一个事件的补充时,它们的总和等于 1。
P(A') + P(A) = 1
或
P(A') = 1 — P(A)
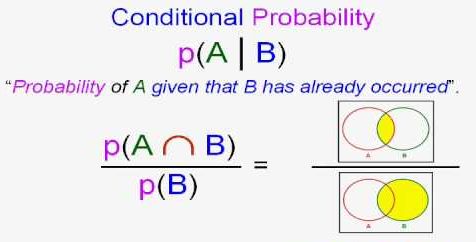
4.3.4 条件概率
条件概率是指在另一个事件已经发生的情况下,一个事件发生的概率。
条件概率的公式由条件概率的乘法规则给出:
哪里:
- P(A |B) 是给定事件 B 的事件 A 的条件概率。
- P(A ∩ B) 是事件 A 和 B 交集(两个事件都发生)的概率。
- P(B) 是事件 B 发生的概率。
例:
一个罐子里有4个绿色弹珠和6个黄色弹珠。从罐子里抽出了两个弹珠。第二颗大理石已经绘制出来,没有更换。两个绘制的弹珠都是黄色的概率是多少?
溶液
设 A = 第一个弹珠为黄色的事件;并设 B = 第二个弹珠为黄色的事件。我们知道以下内容:
- 一开始,盒子里有 10 个弹珠,其中 6 个是黄色的。因此,P(A) = 6/10
- 第一次选择后,罐子里有 9 个弹珠,其中 5 个是黄色的。因此,P(B|A) = 5/9
因此,根据乘法规则:
P(A∩B) = P(A)。P(B∣A)P(A∩B) = (6/10)∗(5/9)
= 30/90 = 1/3 = 0.33
五、贝叶斯定理
贝叶斯定理描述了基于可能与事件相关的条件的先验知识的事件概率。
似乎令人困惑?不用担心!我会让你变得简单。
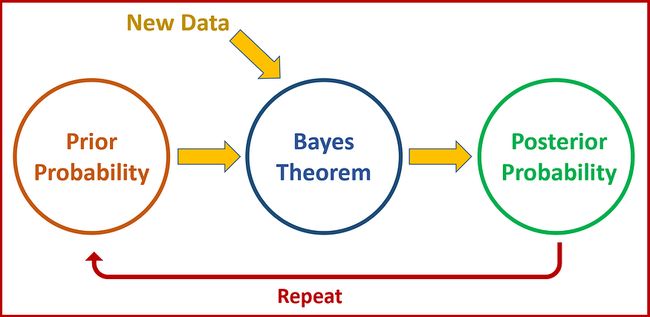
贝叶斯定理作为一个逻辑框架,将新证据纳入我们现有的信念,使我们能够做出更明智的决定。它提供了一种系统的方法,可以在我们遇到新数据、观察或测试结果时更新概率。
它是概率论中最显着的发展之一,将人类认知纳入其应用。正如人类用新的经验来调整他们的信念一样,贝叶斯定理在结合一条新证据后增强了概率。
5.2 让我们举一个例子:
想象一下,您是一名医生,面临着诊断患者的疾病。根据您的经验和知识,您对不同疾病的可能性有先验信念(先验概率)。现在,患者已经接受了诊断测试(新证据),该测试提供了某些测试结果(条件概率)。您需要更新您的初始信念(先验概率)以得出更准确的诊断(后验概率)。
5.3 数学之旅:从先验概率到后验概率
但是它如何在数学上更新概率呢?让我们理解这一点。
在这里,P(A) = 在任何证据存在之前假设(先验知识)为真的概率。
P(B) = 通过考虑证据变量的所有可能值来计算事件 B 的概率
P(B|A) = 看到给定假设的证据的概率为真。
P(A|B) = (后验)-给定证据的假设概率为真。
注意:由于存在先验事件或信念,因此事件A和B是独立的事件。
注意:分母 (P(B)) 充当归一化因子,确保概率总和为 1。
让我们通过一个数值示例来逐步说明贝叶斯定理。
六、考虑一个医疗场景,其中患者正在接受罕见疾病的检测。
假设我们有以下信息:
- 先验概率:P(疾病)= 0.01(患者患有该疾病的先验概率为 1%,因为它在一般人群中是一种罕见疾病。
- 灵敏度:P(阳性测试结果 |疾病)= 0.95(诊断测试的灵敏度为95%,这意味着在患者实际患有疾病的情况下获得阳性测试结果的概率。
- 特异性:P(阴性检测结果 |无疾病)= 0.90(诊断测试的特异性为 90%,这意味着在患者没有疾病的情况下获得阴性测试结果的概率。
现在,患者接受诊断测试,测试结果为阳性(事件B)。我们想计算患者实际患有该疾病的概率(事件 A |B).
第 1 步:从先验概率开始:P(疾病) = 0.01
第 2 步: 计算可能性:P(阳性测试结果 |疾病) = 0.95
第 3 步: 计算边际概率:P(阳性测试结果)= P(阳性测试结果 |疾病) * P(疾病) + P(阳性测试结果 |无疾病) * P(无疾病) = 0.95 * 0.01 + (1–0.90) * (1–0.01) = 0.0495 + 0.009 = 0.0585
第 4 步:应用贝叶斯定理:P(疾病 |阳性检测结果) = (P(阳性检测结果 |疾病) * P(疾病)) / P(阳性检测结果) = (0.95 * 0.01) / 0.0585 = 0.0095 / 0.0585 ≈ 0.1624
第 5 步: 获得后验概率:P(疾病 |阳性测试结果) ≈ 0.1624
在这个例子中,尽管测试结果为阳性,但患者实际患有该疾病的概率仅为16.24%左右。然而,患有这种疾病的先前信息仅为1%,尽管在给出证据后,它有所增加。
虽然,对于被诊断患有某种疾病的人来说,它仍然很低。疾病的先验概率低,检验精度不高,导致后验概率相对较低。因此,这让我们想到测试实验室的概率可能不太准确。
所以,这就是我这篇文章的结尾,涵盖了概率论的基础知识。