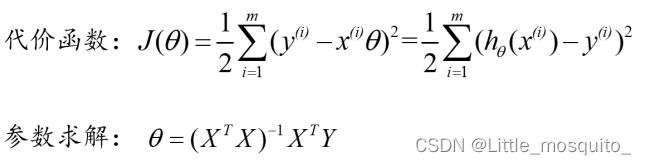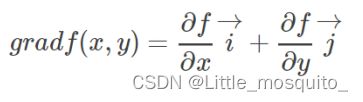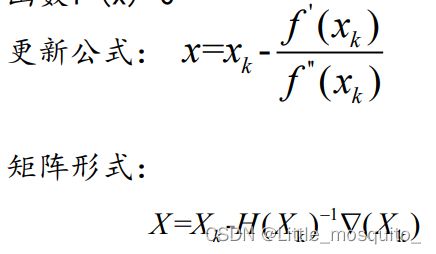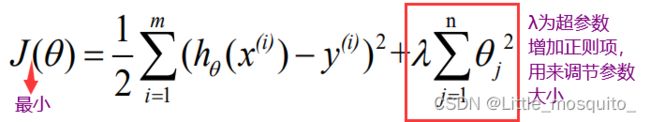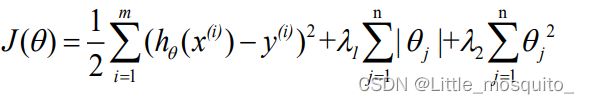机器学习：线性回归

一、线性回归&最小二乘法

1、回归

• 回归：了解两个或多个变量间是否相关、及其相关方向与强度，并建立数学模型来预测变量；
• 回归分析可以由给出的自变量估计因变量的条件期望；
• 找到最合适的一个超平面来拟合我们的数据点；

2、数学推导：x0 = 1

3、误差分布

误差是独立并且具有相同的分布，服从均值为0，方差为σ2的高斯分布；

4、最小二乘法推导

推导过程：https://download.csdn.net/download/Little_mosquito_/86746462

5、最小二乘法代码实现线性回归

jupyter notebook目录安装_修沟的修勾在修沟的博客-CSDN博客_jupyter安装目录

import warnings
warnings.filterwarnings("ignore") # 忽略警告
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# 读取文件
data=pd.read_csv(r"C:\Users\Administrator\Desktop\jqxx\data_line.txt",sep='	',names=['x1','y'])
data['x0']=1
feature=data[['x0','x1']]  # 特征
label=data['y']            # 标签
 
#画原始数据图
plt.figure(figsize=(8,4),dpi=100)   # inch，100   dpi：分辨率
plt.scatter(data['x1'],label,color='black')  # 原始数据
plt.title("original_data")

#最小二乘法求解系数
feature_matrix=np.mat(feature)   # 转为矩阵，X
label_matrix=np.mat(label).T     # 转置变成一列
theta = (feature_matrix.T * feature_matrix).I * feature_matrix.T * label_matrix
y_predict=feature_matrix * theta
plt.figure(figsize=(8,4),dpi=100)
plt.scatter(data['x1'],label,color='black')               # 原始数据
plt.plot(data['x1'],y_predict,color ='blue',linewidth=3)  # 拟合曲线
plt.title("least_square")

6、最小二乘法回归的问题：

• 矩阵必须可逆；
• 当特征数较多时，求逆运算时间开销较大；

二、梯度下降法

1、原理：

使得代价函数达到最小的经典方法之一；

2、梯度

函数z=f(x,y)在点P沿哪个方向变化的速率最大，这个方向就是梯度的方向；

z=f(x,y) 在 点 P(x,y) 处 的梯 度方 向 与 点 P 的等高线 f(x,y)=c在这点的法向量的方向相同，且从数值较低的等高线指向数值较高的等高线；

3、梯度下降法

4、代码实现

4.1、梯度下降法理解：

import numpy as np
%matplotlib inline
# 构建函数
x = np.linspace(-5,9)
y = x**2-4*x

# 梯度下降法求解最小值
def f_prime(x_old):         # f(x)的导数
    return 2 * x_old - 4
x_old = -200                # 初始值
alpha = 0.001               # 步长，也就是学习速率，控制更新的幅度
for i in range(10000):      # 参数循环迭代
    x_new = x_old - alpha * f_prime(x_old)
    x_old = x_new 
print(x_new)

4.2、梯度下降法求最小值：

#梯度下降法
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
# y = kx + b,k is slope, b is y-intercept

#更新一次，单次迭代
def step_gradient(b_current, k_current, points, learningRate):
    b_gradient = 0
    k_gradient = 0
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        k_gradient += (((k_current * x) + b_current)-y)*x
        b_gradient += (((k_current * x) + b_current)-y)*1
    new_b = b_current - (learningRate * b_gradient)
    new_k = k_current - (learningRate * k_gradient)
    return [new_b, new_k]

#误差函数 ，单次迭代后计算误差
def compute_error_for_line_given_points(b, k, points):
    totalError = 0
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        totalError += (y - (k * x + b)) ** 2
    return totalError/len(points)


#多次迭代
def gradient_descent_runner(points, starting_b, starting_k, learning_rate, num_iterations):
    b = starting_b
    k = starting_k
    error=[]
    for i in range(num_iterations):  #迭代多少次
        b, k = step_gradient(b, k, np.array(points), learning_rate) #单次迭代
        error.append(compute_error_for_line_given_points(b, k, points))
    return [b, k,error]
    

#画原始数据图
points = np.array(pd.read_csv(r"C:\Users\Administrator\Desktop\jqxx\data.csv", delimiter=",",names=['x1','y']))
plt.figure(figsize=(8,4),dpi=100)
plt.scatter(points[:,0],points[:,1],color='black')
plt.title("original_data")


#梯度下降法
plt.figure(figsize=(8,4),dpi=100)
plt.scatter(points[:,0],points[:,1],color='black')

learning_rate = 0.000001  #学习率
initial_b = 0 # initial y-intercept guess
initial_k = 0 # initial slope guess
num_iterations = 10000
[b, k, error1] = gradient_descent_runner(points, initial_b, initial_k, 0.0000001, num_iterations)
y_predict=points[:,0]*k+b #预测
plt.plot(points[:,0],y_predict,color='blue')
plt.title("GradientDescent")

#迭代次数与误差的关系
plt.figure(figsize=(8,4),dpi=100)
plt.plot(range(num_iterations)[0:1000],np.array(error1)[0:1000],color='blue')
plt.xlabel("iteration number")                                   #添加x轴的名称
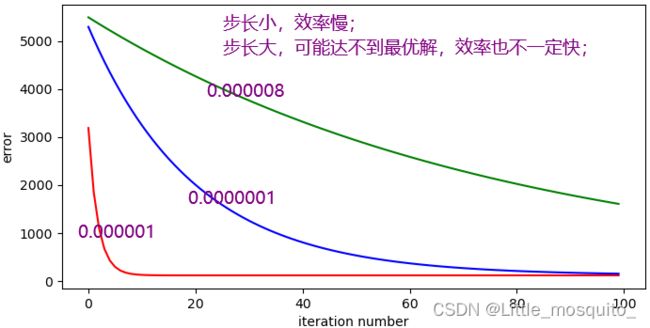
plt.ylabel("error") 

5、算法调优

算法的步长选择：

[b, k, error1] = gradient_descent_runner(points, initial_b, initial_k, 0.000001, num_iterations)
[b, k, error2] = gradient_descent_runner(points, initial_b, initial_k, 0.0000001, num_iterations)
[b, k, error3] = gradient_descent_runner(points, initial_b, initial_k, 0.000008, num_iterations)

# 迭代次数与误差的关系
plt.figure(figsize=(8,4),dpi=100)
plt.plot(range(num_iterations)[0:100],np.array(error1)[0:100],color='red')
plt.plot(range(num_iterations)[0:100],np.array(error2)[0:100],color='blue')
plt.plot(range(num_iterations)[0:100],np.array(error3)[0:100],color='green')
plt.xlabel("iteration number")              
plt.ylabel("error") 

算法参数的初始值选择：

单个初始值可能只能达到局部最优，需要放置多个初始值，迭代选取最优的参数；

归一化：

距离算法（KNN、KMeans）通过归一化消除量纲的影响；

梯度下降，主要是为降低迭代次数，提升迭代效率；

6、分类

批量梯度下降算法：

• 每一次迭代使用全部的样本；
• 能达到全局最优解（凸函数情况下）；
• 当样本数目很多时，训练过程缓慢；

随机梯度下降算法：

• 每一次更新参数只使用一个样 本，进行多次更新；
• 迭代速度快；
• 准确度下降，每次不一定朝着收敛的方向；

***小批量梯度下降算法：

• 更新每一参数时都使用一部分样本来进行更新；
• 参数更新方差更加稳定，每次学习的速度更高；

三、牛顿法

泰勒公式_百度百科

最优化方法之梯度下降法和牛顿法_thatway1989的博客-CSDN博客

常见的几种最优化方法（梯度下降法、牛顿法、拟牛顿法、共轭梯度法等） - 蓝鲸王子 - 博客园

基本原理：利用迭代点Xk处的一阶导数（梯度）和二阶导数 对目标函数进行二次函数近似，然后把二次函数的极小点作 为新的迭代点

四、模型误差

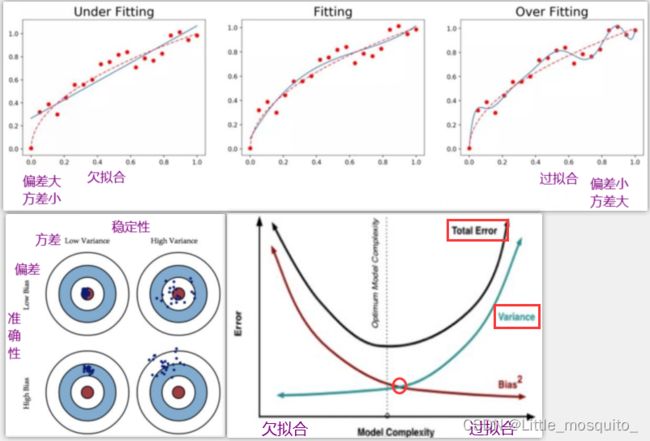
1、模型误差：数据本身 + 偏差 + 方差

• 偏差：度量学习算法的期望预测与真实结果的偏离程度，刻画算法本身的拟合能力；
• 方差：度量同样大小的训练集的变动所导致的学习性能变化，刻画数据扰动所造成的影响；
• 当模型欠拟合时，就会出现较大的偏差；当模型过拟合时，会出现较大的方差；

2、偏差、方差解决思路：

偏差：避免欠拟合

• 寻找更好的特征 -- 具有代表性
• 用更多的特征 -- 增大输入向量的维度（增加模型复杂度）

方差：避免过拟合

• 增大数据集合 -- 使用更多的数据，噪声点比减少（减少数据扰动所造成的影响）
• 减少数据特征 -- 减少数据维度，高维空间密度小（减少模型复杂度）
• 正则化方法
• 交叉验证法

五、岭回归（L2正则化）

1、原理：

• 在平方误差的基础上增加正则项（L2正则），减小参数，避免过拟合；

•  λ>0,通过确定λ的值在模型方差和偏差之间达到平衡，随着λ的增大，模型方差减小而偏差增大；
• 最小二乘法求解岭回归模型参数，可得：

  

2、代码

正则项的理解：

# 特征之间相关
x=np.mat([[1,2],[2,4.1]])   
(x.T*x).I                   # 求逆值较大，导致系数较大
# 特征微小变化导致系数变化较大，模型不稳定，模型过拟合
x=np.mat([[1,2],[2,4.2]])
(x.T*x).I  

#特征不相关
x=np.mat([[1.1,2],[2,4.2]])  
(x.T*x).I                   # 求逆值较小，系数较小  
#特征微小变化导致的系数变化较小，模型稳定
x=np.mat([[1.1,2],[2,4.3]])
(x.T*x).I   

岭回归实现：

# 岭回归
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
def load_data():
    data=pd.read_table('data_ridge.txt',sep='	',names=['x1','y'])
    data['x0']=1
    feature=data[['x0','x1']]
    label=data['y']
    return np.mat(feature), np.mat(label).T

def ridge_regression(feature, label, lam):
    n = np.shape(feature)[1]
    theta = (feature.T * feature + lam * np.mat(np.eye(n))).I * feature.T * label
    return theta

# 导入数据
feature, label = load_data()
plt.figure(figsize = (8,4),dpi = 100)
feature1=feature[:,1].getA()
label1 = label.getA()             # 从矩阵里面取数组
plt.scatter(feature1,label1,color = 'black')

# 训练模型
theta = ridge_regression(feature, label, 0.0001)  
y_fit = feature * theta
plt.plot(feature1,y_fit,color ='blue',linewidth=3)
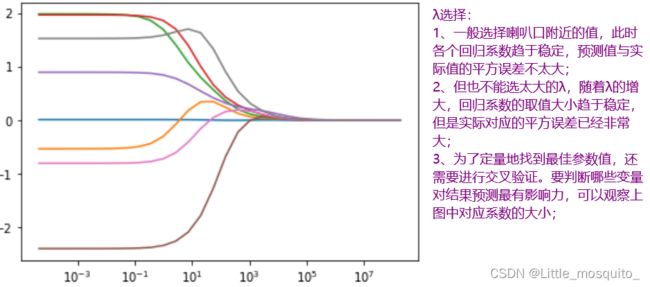
plt.title("ridge_regression")

曲线绘制：

# 岭回归系数选择
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from math import exp
def load_data():
    data=pd.read_table('abalone.txt',sep='	',names=['x1','x2','x3','x4','x5','x6','x7','x8','y'])
    feature=data.loc[:,'x1':'x8']
    label=data['y']
    return np.mat(feature), np.mat(label).T

def standarize(X):
    std_deviation = np.std(X)
    mean = np.mean(X)
    return (X - mean)/std_deviation

def ridge_regression(X, y, lambd=0.2):
    m,n = X.shape
    I = np.matrix(np.eye(n))
    w = (X.T*X + lambd*I).I*X.T*y
    return w

def ridge_traj(X, y, k=20):
    m, n = X.shape
    ws = np.zeros((k, n))
    for i in range(k):
        w = ridge_regression(X, y, lambd=exp(i-10))
        ws[i, :] = w.T
    return ws

# 加载数据
X, y = load_data()
# 标准化
X, y = standarize(X), standarize(y)
# 绘制岭轨迹
k = 30
ws = ridge_traj(X, y, k)
lambdas = [exp(i-10) for i in range(k)]
plt.semilogx(lambdas, ws)
plt.show()

六、Lasso回归

1、原理

• 在平方误差的基础上增加正则项（L1正则）：

• λ>0，通过确定λ值使得在方差和偏差之间达到平衡，随着λ值的增大，模型方差减小而偏差增大；
• 与L2正则的不同，损失函数在参数=0处是不可导，因此基于梯度的方法不能直接用于损失函数的求解；

2、坐标轴下降法

• 坐标轴下降法沿着坐标轴的方向去下降（非梯度负方向），通过一步步迭代求解函数的最小值；
• 坐标轴下降在整个过程中依次循环使用不同的坐标方向进行迭代，一个周期的一维搜索迭代过程相当于一个梯度下降的迭代；

import itertools
from math import exp
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def load_data():
    data=pd.read_table('abalone.txt',sep='	',names=['x1','x2','x3','x4','x5','x6','x7','x8','y'])
    feature=data.loc[:,'x1':'x8']
    label=data['y']
    return np.mat(feature), np.mat(label).T

def standarize(X):
    ''' 标准化数据 (零均值, 单位标准差)
    '''
    std_deviation = np.std(X)
    mean = np.mean(X)
    return (X - mean)/std_deviation

def lasso_regression(X, y, lambd=0.2, threshold=0.1):
    ''' 通过坐标下降(coordinate descent)法获取LASSO回归系数
    '''
    # 计算残差平方和
    rss = lambda X, y, w: (y - X*w).T*(y - X*w)

    # 初始化回归系数w.
    m, n = X.shape
    w = np.matrix(np.zeros((n, 1)))
    r = rss(X, y, w)

    # 使用坐标下降法优化回归系数w
    niter = itertools.count(1)

    for it in niter:
        for k in range(n):
            # 计算常量值z_k和p_k
            z_k = (X[:, k].T*X[:, k])[0, 0]
            p_k = 0
            for i in range(m):
                p_k += X[i, k]*(y[i, 0] - sum([X[i, j]*w[j, 0] for j in range(n) if j != k]))

            if p_k < -lambd/2:
                w_k = (p_k + lambd/2)/z_k
            elif p_k > lambd/2:
                w_k = (p_k - lambd/2)/z_k
            else:
                w_k = 0

            w[k, 0] = w_k

        r_prime = rss(X, y, w)
        delta = abs(r_prime - r)[0, 0]
        r = r_prime
        #print('Iteration: {}, delta = {}'.format(it, delta))

        if delta < threshold:
            break

    return w

def lasso_traj(X, y, k=20):
    ''' 获取回归系数轨迹矩阵
    '''
    m, n = X.shape
    ws = np.zeros((k, n))
    for i in range(k):
        w = lasso_regression(X, y, lambd=exp(i-10))
        ws[i, :] = w.T
        #print('lambda = e^({}), w = {}'.format(i-10, w.T[0, :]))
    return ws


X, y = load_data()
X, y = standarize(X), standarize(y)
w = lasso_regression(X, y, lambd=10)
# 绘制轨迹
k = 20
ws = lasso_traj(X, y, k)
fig = plt.figure()
lambdas = [exp(i-10) for i in range(k)]
plt.semilogx(lambdas, ws)
plt.show()

七、弹性网

• 使用L1和L2作为正则化矩阵的线性回归模型，是岭回归和Lasso回归的组合；
• 弹性网结合了岭回归的计算精准的优点，同时又结合了Lasso回归特征选择的优势；

三种方法的选择：

• 岭回归优缺点：计算精准（没有丢失特征），不具备特征选择功能；
• Lasso回归优缺点：具有特征选择功能，但是将某些θ化为0，可能导致特征丢失，使得最终的模型的偏差比较大；
• 在进行正则化的过程中，通常要先使用岭回归
• 当特征非常多时，尤其当多个特征和另一个特征相关的时弹性网非常有用；

八、sklearn：线性回归

算法库：

https://scikit-learn.org/stable/

1、标准线性回归

# 标准线性回归
from sklearn import linear_model
reg = linear_model.LinearRegression()         # 创建模型：用默认参数即可
reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])  # 训练，拟合
reg.predict([[4,4],[5,6]])                    # 预测

reg.coef_       # 系数
reg.intercept_  # 截距

2、岭回归

from sklearn import linear_model
reg = linear_model.Ridge(alpha=0.5)          # 需要优化alpha参数
reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1]) 
reg.predict([[4,4],[3,4]])                   # 预测

3、lasso回归

from sklearn import linear_model
reg = linear_model.Lasso(alpha=0.1)
reg.fit([[0, 0], [1, 1]], [0, 1])
reg.predict([[1, 1]])

 4、弹性网

from sklearn.linear_model import ElasticNet
reg = ElasticNet(alpha=1.0,l1_ratio=0.5)     # 需要优化alpha和l1_ratio
reg.fit([[0, 0], [1, 1]], [0, 1])
reg.predict([[1, 1]])

九、模型优化：交叉验证+网格搜索

• 训练集：训练模型；
• 验证集：优化超参数；   --  交叉验证 + 网格搜索
• 测试集：评估模型的泛化能力；

1、岭回归：

from sklearn import linear_model
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import GridSearchCV
def load_data():
    data=pd.read_csv(r'D:\CDA\File\abalone.txt',sep='	',names=['x1','x2','x3','x4','x5','x6','x7','x8','y'])
    feature=data.loc[:,'x1':'x8']
    label=data['y']
    return np.mat(feature), np.mat(label).T
X, y = load_data()
X, y = StandardScaler().fit_transform(X), StandardScaler().fit_transform(y)  # 标准化
params={'alpha':[0.001,0.01,0.1,1,10,100]}                                   # 粗调节，确定数量级
ridge = linear_model.Ridge()
grid_search=GridSearchCV(ridge,param_grid=params,cv=10,verbose=2,n_jobs=-1) # verbose：日志信息
grid_search.fit(X, y)
grid_search.best_params_

params={'alpha':np.arange(1,25)}                # 细调节
ridge = linear_model.Ridge()#
grid_search=GridSearchCV(ridge,params,cv=10,verbose=2,n_jobs=-1)
grid_search.fit(X, y)
grid_search.best_params_

2、弹性网

from sklearn.linear_model import ElasticNet
params = {'alpha':[0.00001,0.001,0.01,0.1,1,10,100],'l1_ratio':[0.1,0.2,0.3,0.4,0.5]}
elasticNet = ElasticNet()
grid_search = GridSearchCV(elasticNet,param_grid=params,cv=10,verbose=2,n_jobs=-1)
grid_search.fit(X, y)
grid_search.best_params_

params = {'alpha':np.linspace(0.001,0.1,10),'l1_ratio':np.linspace(0.1,0.3,10)}
elasticNet = ElasticNet()
grid_search = GridSearchCV(elasticNet,param_grid=params,cv=10,verbose=2,n_jobs=-1)
grid_search.fit(X, y)
grid_search.best_params_

十、波士顿房价预测

• 波士顿房价数据集（Boston House Price Dataset）
• 该数据集是一个回归问题。每个类的观察值数量是均等的，共有 506 个观察，13 个输入变量和1个输出变量。
• 每条数据包含房屋以及房屋周围的详细信息。其中包含城镇犯罪率，一氧化氮浓度，住宅平均房间数，到中心区域的加权距离以及自住房平均房价等等。
• CRIM：城镇人均犯罪率。
• ZN：住宅用地超过 25000 sq.ft. 的比例。
• INDUS：城镇非零售商用土地的比例。
• CHAS：查理斯河空变量（如果边界是河流，则为1；否则为0）。
• NOX：一氧化氮浓度。
• RM：住宅平均房间数。
• AGE：1940 年之前建成的自用房屋比例。
• DIS：到波士顿五个中心区域的加权距离。
• RAD：辐射性公路的接近指数。
• TAX：每 10000 美元的全值财产税率。
• PTRATIO：城镇师生比例。
• B：1000（Bk-0.63）^ 2，其中 Bk 指代城镇中黑人的比例。
• LSTAT：人口中地位低下者的比例。
• MEDV：自住房的平均房价，以千美元计。

1、加载数据集

from sklearn.linear_model import LinearRegression, Ridge,Lasso
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt 
from sklearn.metrics import mean_squared_error

ld = load_boston()

2、拆分数据集&标准化

# 拆分数据集
x_train,x_test,y_train,y_test = train_test_split(ld.data,ld.target,test_size=0.25)
# 标准化
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)

3、标准线性回归

lr = LinearRegression().fit(x_train,y_train)
y_lr_predict = lr.predict(x_test)
print("lr的均方误差为：",mean_squared_error(y_test,y_lr_predict))
plt.figure(figsize=(8,4),dpi=100)
plt.title("LinearRegression")
plt.plot(y_test,y_lr_predict, 'rx')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'b-.', lw=4)  #  y=x
plt.ylabel("Predieted Price")
plt.xlabel("Real Price")
plt.show()

4、岭回归

params={'alpha':[0.001,0.01,0.1,1,10,100]}  # 粗调节
ridge = Ridge()
grid_search=GridSearchCV(ridge,param_grid=params,cv=10)
grid_search.fit(x_train,y_train)
grid_search.best_params_

y_rd_predict = grid_search.predict(x_test)
print("Ridge的均方误差为：",mean_squared_error(y_test,y_rd_predict))
plt.figure(figsize=(8,4),dpi=100)
plt.title("RidgeRegression")
plt.plot(y_test,y_lr_predict, 'rx')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'b-.', lw=4)
plt.ylabel("Predieted Price")
plt.xlabel("Real Price")
plt.show()

5、lasso回归

params={'alpha':[0.001,0.01,0.1,1,10,100]}     # 粗调节
ridge = Lasso()
grid_search=GridSearchCV(ridge,param_grid=params,cv=10)
grid_search.fit(x_train,y_train)
grid_search.best_params_

y_rd_predict = grid_search.predict(x_test)
print("Lasso的均方误差为：",mean_squared_error(y_test,y_rd_predict))
plt.figure(figsize=(8,4),dpi=100)
plt.title("RidgeRegression")
plt.plot(y_test,y_lr_predict, 'rx')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'b-.', lw=4)
plt.ylabel("Predieted Price")
plt.xlabel("Real Price")
plt.show()