从2-3树谈到左倾红黑树
2-3树
定义
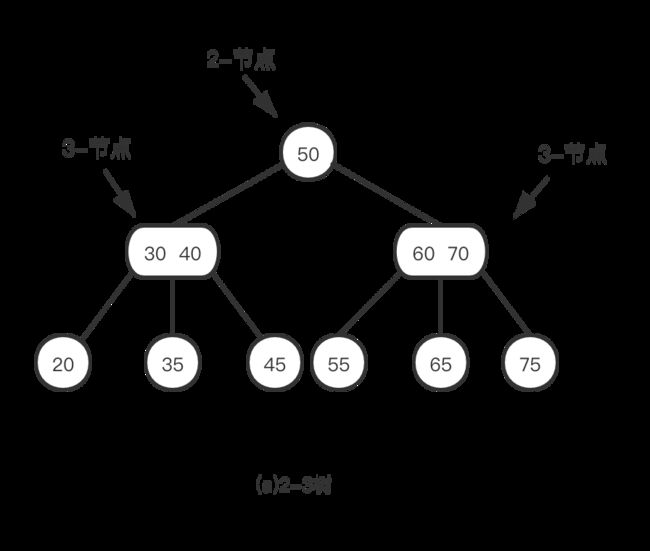
顾名思义，2-3树，就是有2个儿子或3个儿子的节点。2-3树就是由这些节点构成。所以2-3-4树的每个节点都是下面中的一个：
- 空节点：空节点。
- 2-节点：包含一个元素和两个儿子。
- 3-节点：包含二个元素和三个儿子。
2-3树是有序的：每个元素必须大于或等于它左边的任何元素。
操作
2-3 树实现起来相对困难，因为在树上的操作涉及大量的特殊情况。2-3树可以用一种左倾红黑树来替代(后面会发现2-3树和左倾红黑树是等价的)，实现起来更简单一些，所以用它来替代（左倾红黑树稍后介绍）。
查找
查找可以分为以下几个步骤：
- 先将它和根节点的的值就行比较，如果它和其中任意一个相等，查找命中。
- 根据左小右大的原则，找到指向相应区间的链接，并在其指向的子树中递归地继续查找。
- 如果是空链接，则查找未命中。
查找具体过程如下：
插入
可以看到2-3树的节点不像其他的树一个节点只有一个值，所以插入会有4种不同的情况：
- 向2-节点插入新值。
- 向一颗只有一个3-节点的树插入新值。
- 向一个父结点为2-节点的3-节点插入新值。
- 向一个父结点为3-节点的3-节点插入新值。
二叉查找树的插入是先进行一次未命中的查找，然后把要插入的节点插入到树的底部。但是这样的树就无法保持完美的平衡(所有空链接到根结点的距离都是相同的)了。2-3树可以做到插入后继续保持平衡。
插入情形一(向2-节点插入新值)
查找80，没有查找到80，则在含有75的节点中插入80，
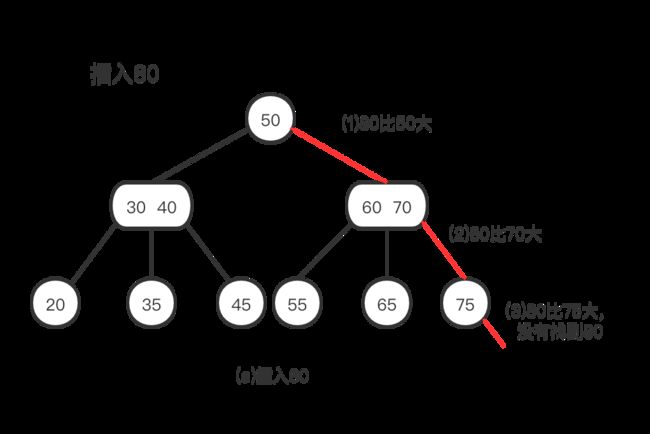
我们怎么插入才可以保持2-3树的完美平衡呢？我们可以把2-节点变成一个3-节点。
插入情形二(向一颗只有一个3-节点的树插入新值)
插入80，这颗只有一个3-节点的树只有2个值在节点中，根据2-3树的性质可以做到已经没有位置插入新值。我们把新值插入到3-节点中，变成一个临时的4-节点，然后在把4-节点分解成一个2-3树。
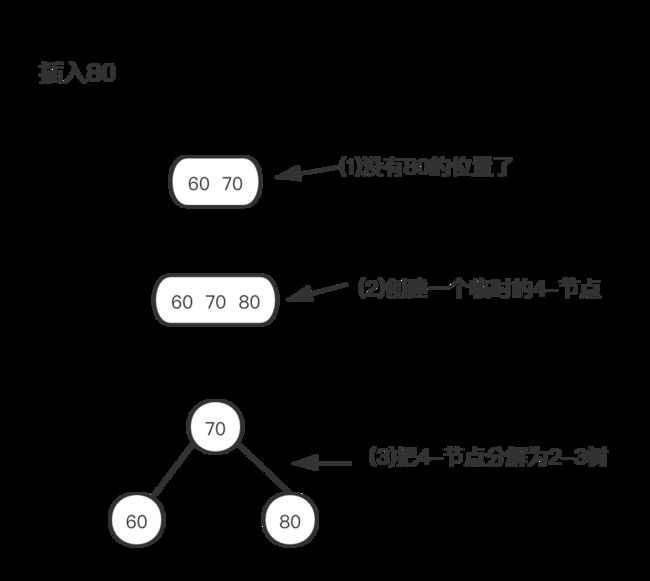
插入情形三(向一个父结点为2-节点的3-节点插入新值)
查找80，没有查找到80，则在含有70、75的节点中插入80，这个节点是一个3-节点已经插入不进值了。
所以我们创建一个临时的4-节点，分解把中值移到父节点。在分解剩下的成两个2-节点。
插入情形四(向一个父结点为3-节点的3-节点插入新值)
插入情形四的处理可以说是包含了情形三和情形二和情形一的处理。按照情形三将3-节点替换为4-节点，然后分解，把它的中节点插入到它的父结点。但父结点也是个3-节点，因此我们在替换为4-节点，然后在这个节点上做相同的变换。一直不停的向上替换为4-节点，在分解，直到遇到一个2-节点并将它替换为一个不需要继续分解的3-节点(情形一的处理)，或者是到达了3-节点的根(情形二的处理)。
我们将临时的4-节点分解为3个2-节点，使得树高加1，如上图右下所示。我们可以发现这次的变化仍然保持了树的完美平衡性，因为它变换的是根节点。不是根节点这样变换，就会出现左/右子树比右/左子树高多1。
例子
下图是逐步在2-3树中依次插入10、40、70、30、60、20和50。
删除
删除节点比较复杂，如果不太关心删除的话可以不看删除的，直接看下面的"左倾红黑树"，看到左倾红黑树中的"删除"在回来看这里。
删除最小值
根据性质我们可以知道最小键就是树的左下角。我们分节点来讨论删除的情况：
- 2-节点：从2-节点删除一个键会留下一个空节点，这样就破坏了树的完美平衡性。
- 3-节点：从3-节点删除一个键，3-节点就变成了2-节点，这是可以接受的。
删除2-节点时，为了保证不会破坏树的完美平衡性，我们要让2-节点变成3-节点或4-节点。我们来看一下下面这个例子，根据2-3树的大小关系定义，我们可以把它铺平(b)(实际上不是这样操作的，只是感觉这样说清楚一点)，然后重构(c)，就发现最小值中的2-节点变成了4-节点，将最小值删除就变成3-节点(d)。我们要做的事情就是这种，下面我们一一分析各种情况下的转换。
我们可以把整棵树分为树根、树中和树底。
树根：如果根是2-节点且它的两个子节点都是2-节点，我们可以直接将这三个节点变成一个4-节点。否则我们需要保证根节点的左子节点不是2-节点。怎么保证呢？像上面提到的我们利用2-3树的大小关系，从右侧的兄弟节点借一个节点，因为大小关系，右侧兄弟节点是无法直接移到左侧节点(左<根<右)，我们可以把右侧节点最小的节点移到根节点，在把根节点最小的移到左侧节点。
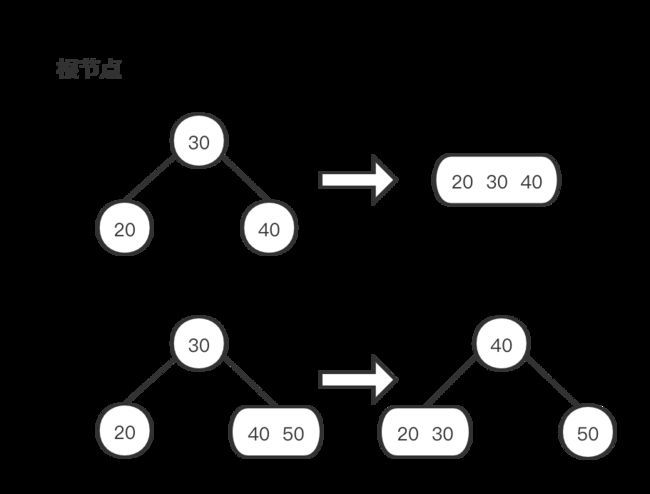
树中：在沿着左链接向下的过程中，需要保证以下情况之一成立：
- 当前节点的左子节点不是2-节点。不用处理
- 当前节点的左子节点是2-节点而它的兄弟节点不是2-节点。处理：从兄弟节点借一个节点，和上图提到的差不多。
- 当前节点的左子节点和它的兄弟节点都是2-节点。处理：将左子节点、当前结点中的最小节点和左子节点最近的兄弟节点合并成一个4-节点。
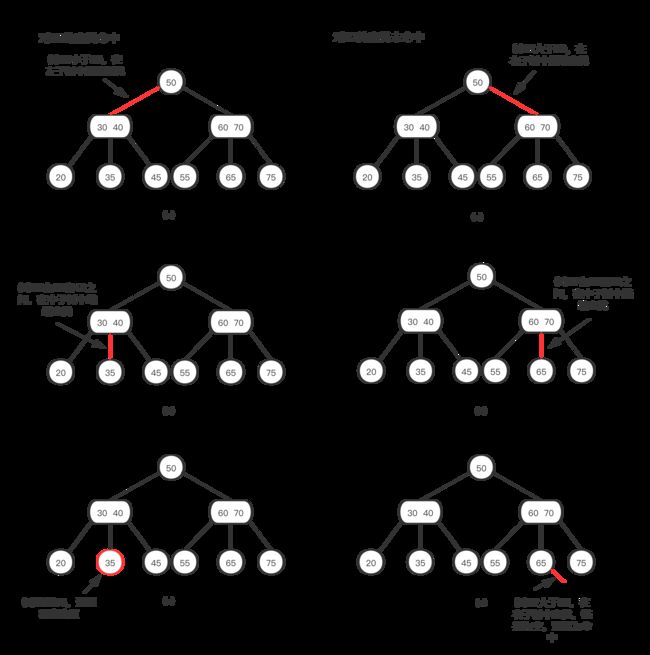
情况二：当前节点的左子节点是2-节点而它的兄弟节点不是2-节点。如下图：
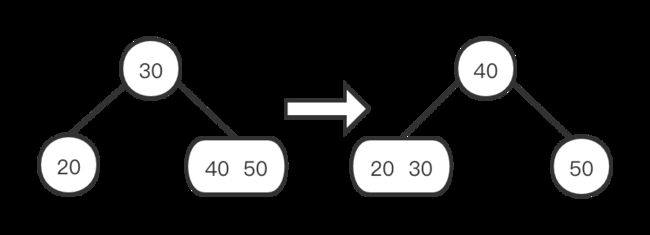
情况三：当前节点的左子节点和它的兄弟节点都是2-节点，将左子节点、当前节点中的最小节点和左子节点最近的兄弟节点合并成一个4-节点。如下图：
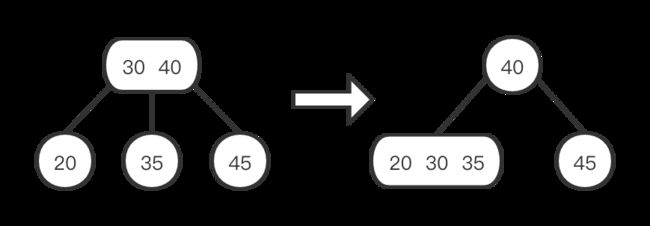
或许有人会奇怪，为什么情况三不能和情况二一样来处理，我们来看一下情况三按情况二来处理是怎么样的，我们会发现35和50的节点少了一个儿子节点，破坏了平衡。
需要注意的就是上面的条件要用于沿着左链接向下的过程中的所有节点。看到这里你有没有疑惑，为什么删除一个节点要那么多节点进行操作？只应用于要删除的节点不可以吗？让我们来看下图中的例子：我们发现因为节点‘10’是个2-节点，就无法处理。如果用于沿着左链接向下的过程中的所有节点，根据情况1，‘10’节点就不可能是个2-节点。硬要处理我们也会发现会破坏树的平衡。
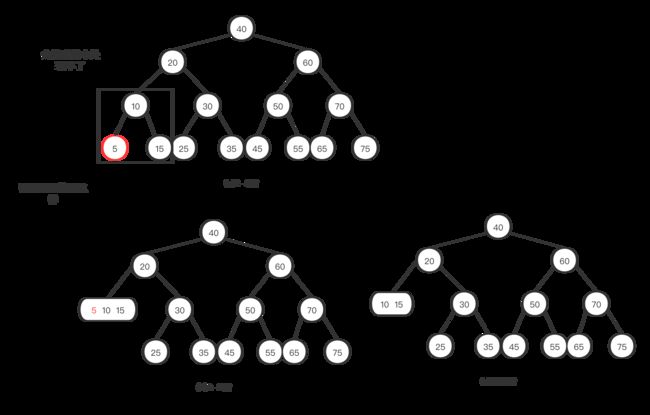
树底：树底就是执行删除的地方了。通过上面的沿着左链接向下的过程中，最后树底左下角会得到一个含有最小值的3-节点或4-节点，我们就可以直接从中将其删除，将3-节点变为2-节点，或者将4-节点变为3-节点。
因为这遍历的过程中，会有临时的4-节点，所以做完删除的操作后，我们还需要回头向上分解所有的临时4-节点。
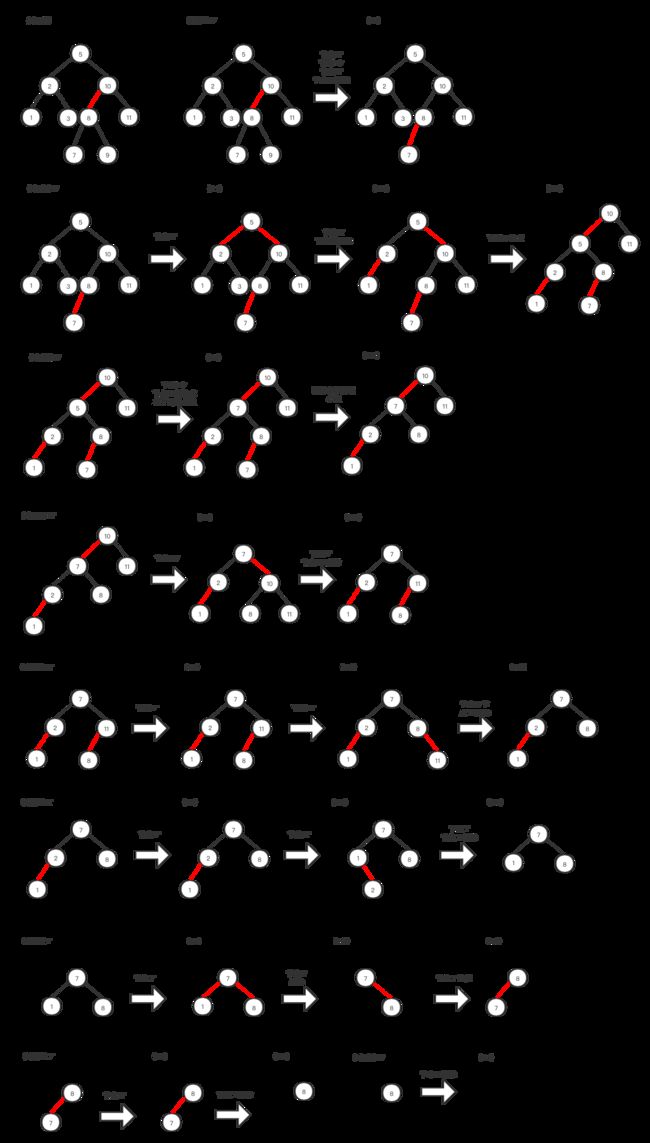
看下面删除最小值的例子：
删除最大值
删除最大和删除最小差不多，直接演示一个例子吧。
删除
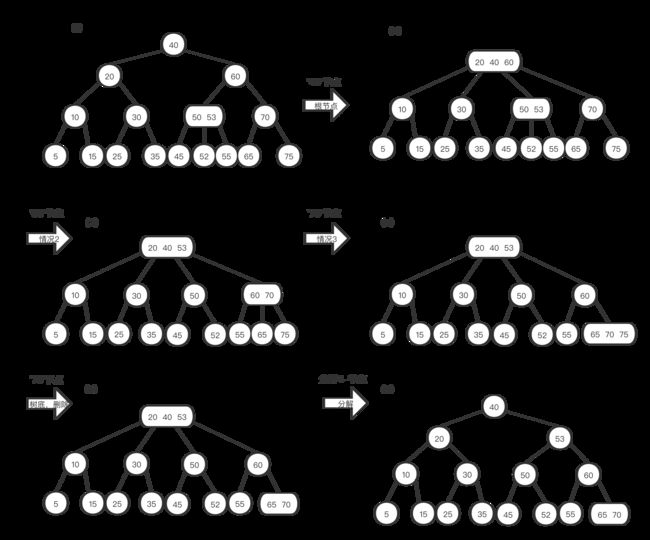
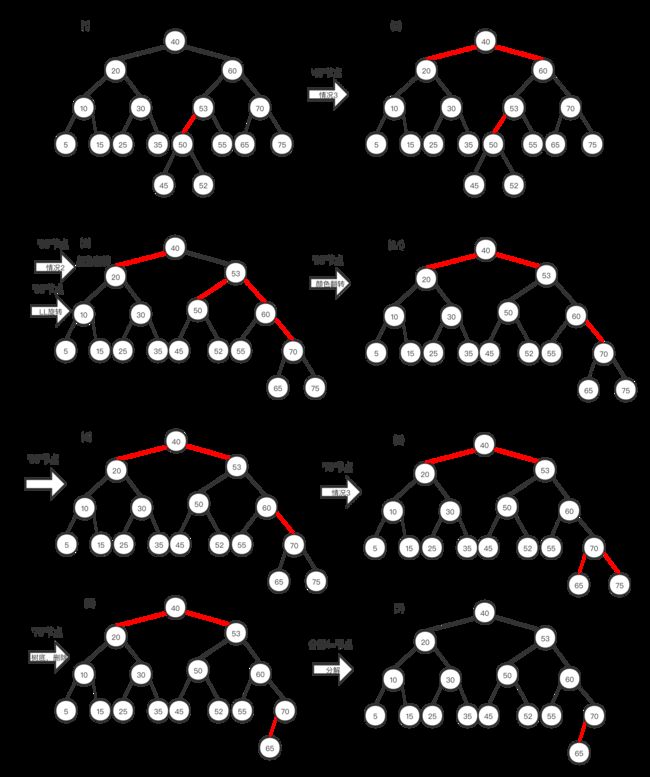
在查找路径上进行和删除最小值相同的变换，可以保证在查找过程中任意当前节点均不是2-节点。如果被查找的值在树的底部就可以直接删除。如果不在，我们需要将其右子树的最小的值代替该节点的值，并删除那个节点(右子树最小)，和二叉查找树的删除一样。因为当前节点肯定不是2-节点，问题已经转化为在一棵根节点不是2-节点的子树中删除最小的值，我们可以使用“删除最小值”的算法，删除之后我们还是需要回头向上分解所有的临时的4-节点。下面是删除60的例子。
左倾红黑树
红黑树是一种二叉查找树。红黑树本质上和2-3树没什么区别，基本思想是用标准的二叉树(2-节点)和一些额外的信息(识别3-节点)来表示2-3树。树中的链接分为两种类型：
- 红链接：两个2-节点红链接起来构成一个3-节点。
- 黑链接：2-3树中的普通链接。
不难发现对于任意的2-3树，通过红和黑链接，我们都可以变换成一棵对应的二叉树。这种方式表示2-3树的二叉树称为红黑树。左倾红黑树即红链接只能是左链接，左倾红黑树比红黑树好理解。
定义
左倾红黑树的另一种定义是含有红黑链接并满足下面这些条件的二叉树：
- 红链接都是左链接。(左倾红黑树)
- 如果一个节点是红色的，那么它的子节点必须是黑色的(没有任何一个节点同时和两条红链接相连)
- 从一个节点到一个null引用的每一条路径必须包含相同数目的黑色节点。
和2-3树是一一对应的。
红链接都是左链接：
因为2-3树没有4-节点所以不会出现下图的情况，2-3-4树对应的红黑树才会有，左倾红黑树没有。
如果一个节点是红色的，那么它的子节点必须是黑色的：
我们先来看一下它的反例，即一个节点同时和两条红链接相连的红黑树转换成2-3树是怎么样的。如下图所示，因为2-3树不存在3-节点，所以反例不成立(左倾红黑树可以这样理解，红黑树就不行了)。
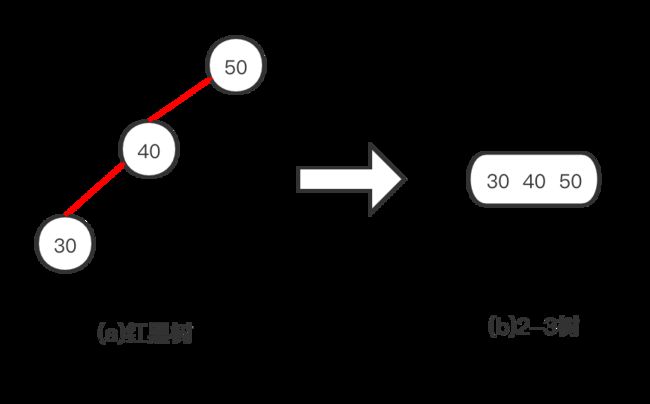
从一个节点到一个null引用的每一条路径必须包含相同数目的黑色节点：
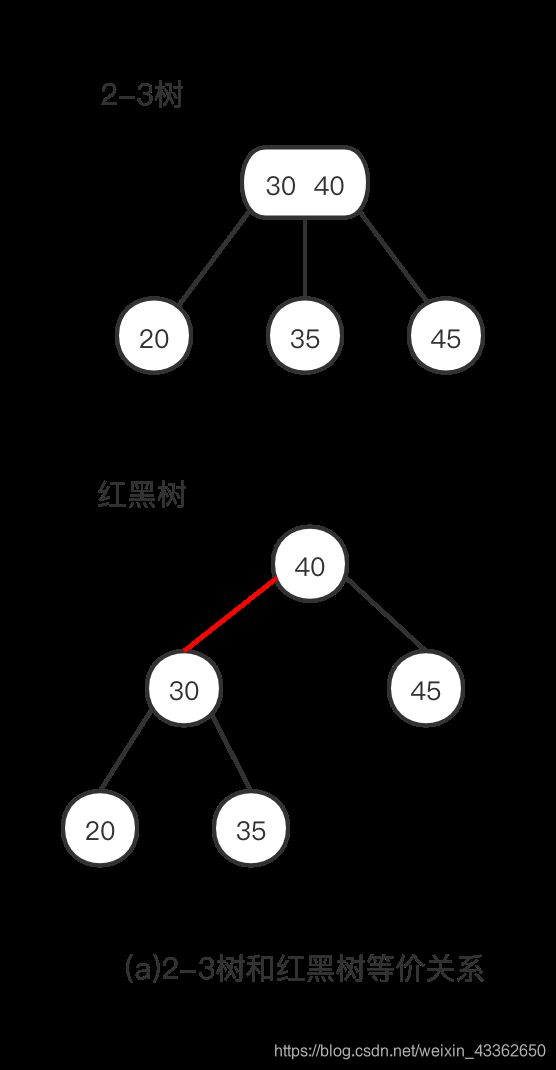
如果从一个节点到一个null引用的每一条路径包含相同数目的黑色节点，我们将一棵红黑树中的红链接画平，那么所有的空链接到根节点的距离都将是相同的，树是完美黑色平衡的，如下图(b)所示。如果我们将红链接相连的节点合并，得到的就是一棵2-3树，所以才说它们是等价的，如下图(c)所示。
根据定义这些链接必然是完美平衡的。红黑树即是二叉查找树，也是2-3树。那么我们就可以把他们的优点结合起来：二叉查找树高效的查找方法和2-3树中高效的插入方法。
代码表示：我们怎么表示红链接和黑链接？每个节点都只会有一条指向自己的链接，我们可以利用这个唯一性。将链接的颜色保存在表示节点的TreeNode数据类型的布尔变量color中。如果指向它的链接是红色该变量为true，黑色则为false。空链接为黑色。即color为true该节点为红色节点，为false该节点为黑色节点。
private class TreeNode{
int data; //值
TreeNode left; //左子树
TreeNode right; //右子树
boolean color; //颜色,true红，false黑
}
操作
为了方便，数据类型直接写死，是int类型，如果需要更改类型，需要注意的只有类型的值比大小。Java泛型可以
public class RedBlackTree<T entends Comparable<? super T>>{
private class TreeNode<T{}
}
有些语言可能没有这种写法，所以我也没有用这种写法，直接int类型。
旋转
在实现一些操作中可能会出现红色右链接或者两条连续的红链接，就会破坏红黑树的性质，为了维持红黑树的性质，要进行旋转，旋转会恢复红黑树的性质。x旋转的细讲可以看这个AVL树。这里不细讲，直接上操作。需要注意的是我们要保留颜色。
LL单旋转：
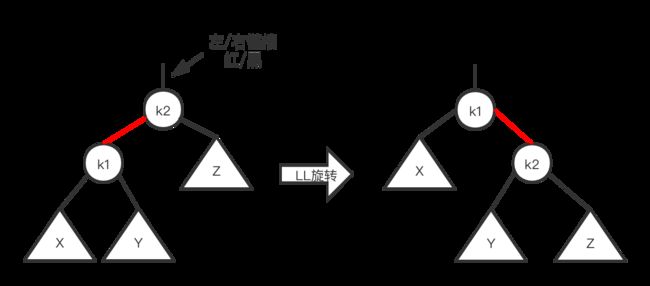
private TreeNode rotateWithLeft(TreeNode k2){
TreeNode k1 = k2.left;
k2.left = k1.right;
k1.right = k2;
k1.color = k2.color;
k2.color = RED;
return k1;
}
RR单旋转：
private TreeNode rotateWithRight(TreeNode k1){
TreeNode k2 = k1.right;
k1.right = k2.left;
k2.left = k1;
k2.color = k1.color;
k1.color = RED;
return k2;
}
插入
插入2种情况：
- 向2-节点中插入新值
- 向一个3-节点中插入新值
插入情形一(向2-节点中插入新值)
插入一个新值在2-节点，有两种可能：
- 新值小于老值，那么就新增了一个红色节点在左子树，和单个3-节点等价。
- 新值大于老值，那么就新增了一个红色节点在右子树，这个时候就要用到上面的LL单旋转，将其旋转为红色左链接。
插入情形二(向3-节点中插入新值)
插入一个新值在3-节点，有三中可能：
- 新值大于原树中的两个值。
- 新值小于用树中的两个值。
- 新值在原树中的两个值之间。
新值大于原树中的两个值：它被链接到3-节点的右链接。如下图所示，我们将两条链接的颜色都由红变黑，就得到了一颗由三个节点组成、高比原树多1的树。可以发现(a)和(c)、(b)和(d)是等价的，正好对应着2-3树的操作。
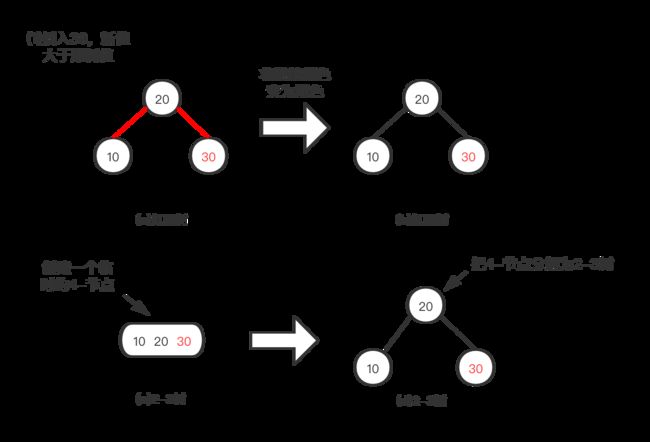
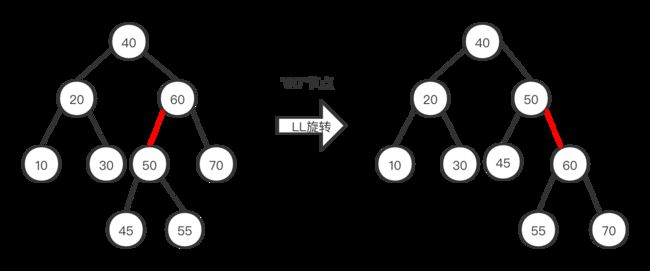
新值小于用树中的两个值：它被链接到最左边，这样就产生了两条连续的红链接，破坏了性质，此时我们就需要进行一次LL旋转即可得到第一种情况(新值大于原树中的两个值)，如下图(b)，按第一种情况处理即可。
新值在原树中的两个值之间：这也会产生两条连续的红链接，破坏了性质，如下图(a)，此时就需要双旋转，先对节点‘10’进行一次RR旋转，图(b)。这个时候就变成第二种情况了(新值小于用树中的两个值)，如下图(b)，按第二种情况处理即可。
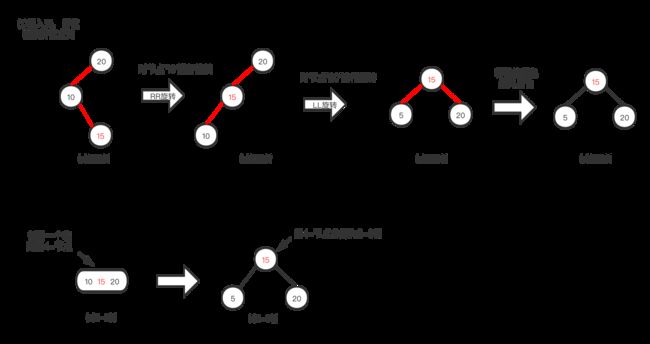
我们会发现不管是情况1、情况2还是情况3，最后都会回到情况1，而且不管是那种情况，对应的2-3树都是一种类型的，这也说明红黑树在处理3-节点时2-3树的本质是一样的。
修复红黑树性质的方法：
private TreeNode balance(TreeNode t){
if (isRed(t.right) && !isRed(t.left)) t = rotateWithRight(t); //有红色右链接便RR旋转
if (isRed(t.left) && isRed(t.left.left)) t= rotateWithLeft(t); //连续两条连续的红链接便LL旋转
if (isRed(t.left) && isRed(t.right)) colorConversion(t); //两个孩子都红链接便颜色转换
return t;
}
颜色翻转
插入时，会经常用到下图中的操作，我们专门写一个方法来转换节点的两个红色子节点的颜色。
写代码前我们先看看下面2-3树的例子，我们可以发现除了两个红色子节点的颜色要转换，它自己的颜色也要转换为红色才符合2-3树是性质。这个性质的背后意义是：不会影响整颗树的黑色平衡。如下图，如果’20’节点不设置为红色，就会破坏红黑树的性质(从一个节点到一个null引用的每一条路径必须包含相同数目的黑色节点)，左边比右边多1条黑色节点。
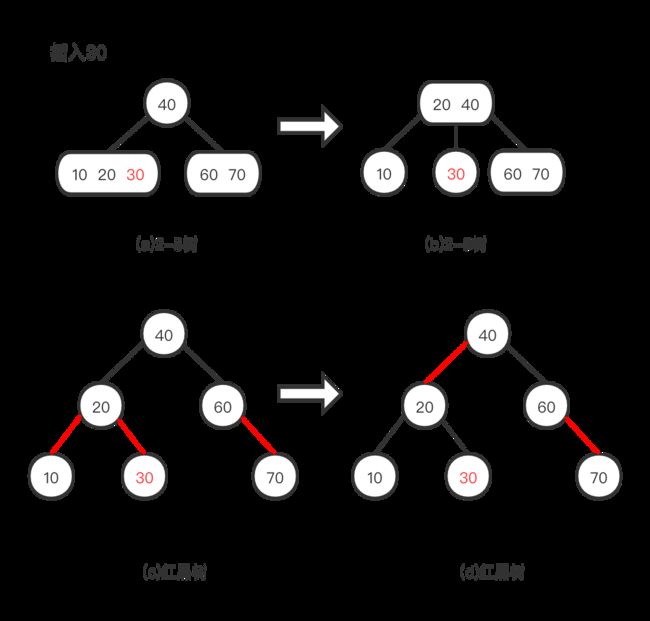
代码：
private void colorConversion(TreeNode node){
node.color = RED;
node.left.color = BLOCK;
node.right.color = BLOCK;
}
有一种情况我们需要注意，就是节点是根节点的时候，这个时候如果使用上面的转换代码就会使根节点变成红色，如下图(b)所示，说明根节点是一个3-节点的一部分，因为根节点之上没有了结点，所以实际情况并不是这样。我们可以得出根节点总是黑色的。因此我们在每次插入后都会将根节点设为黑色。
总结一下上面的操作：
插入代码
就和上面说的一样，一步步操作即可。
- 第一个if：插入情形一(向2-节点中插入新值)
- 第二个if：插入情形二(向3-节点中插入新值)里的情形二(新值小于用树中的两个值)
- 第三个if：颜色转换，插入情形二(向3-节点中插入新值)里的情形一(新值大于原树中的两个值)
- 第一个if+父递归的第二个if：插入情形二(向3-节点中插入新值)里的情形三(新值在原树中的两个值之间)
需要注意的是颜色转换是第三个if，也就是说经过第一个if和第二个if之后，需要颜色转换就会进行颜色转换，这也符合上面提到的：不管是情况1、情况2还是情况3，最后都会回到情况1。
public void insert(int data){
root = insert(root,data);
root.color = BLOCK; //每次插入后根节点都要设置为黑色
}
private TreeNode insert(TreeNode t,int data){
if (t == null){return new TreeNode(data,RED);} //插入，和父节点用红链接相连
if (data < t.data){
t.left = insert(t.left,data);
}else if (data > t.data) {
t.right = insert(t.right,data);
}else ;
return balance(t);
}
例子
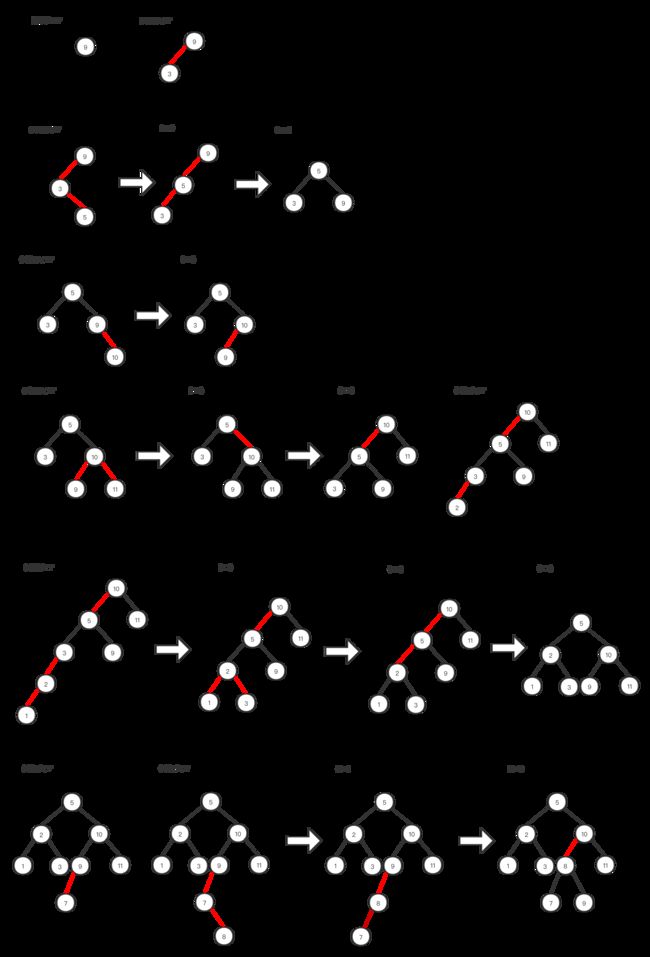
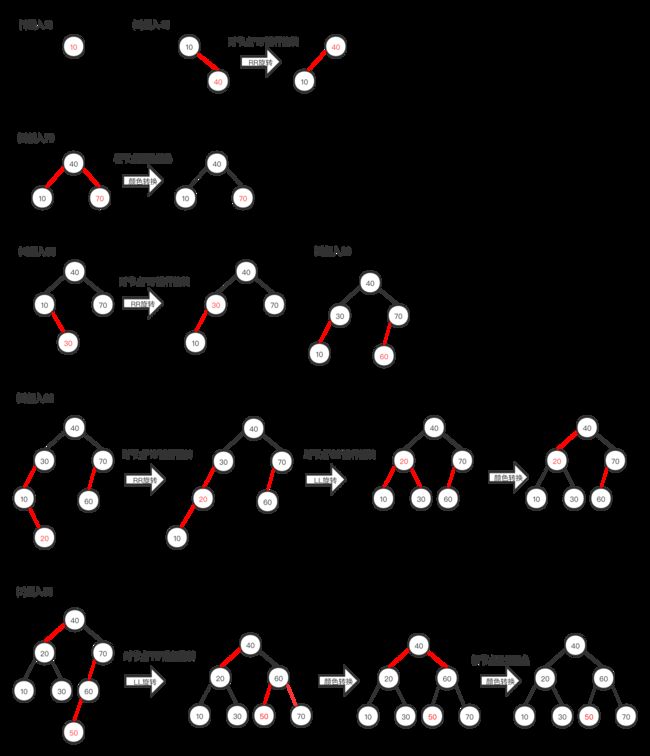
下图是逐步在左倾红黑树中依次插入10、40、70、30、60、20和50(和2-3树插入例子一样)。
删除
红黑树的删除就如2-3树谈到的一般，我们只需要把2-3树谈到的逻辑转换为红黑树的代码就完成了。
删除最小值
根据2-3树中的删除最小值，我们一直沿着左节点递归处理节点，我们需要转换的代码有下面这些：
- 当前节点左子树为空时，表示当前节点就是最小节点。处理：删除该节点。
- 当前节点的左子节点是2-节点而它的兄弟节点不是2-节点。处理：从兄弟节点借一个节点。
- 当前节点的左子节点和它的兄弟节点都是2-节点。处理：将左子节点、当前结点和左子节点最近的兄弟节点合并成一个4-节点。
还记得我们在2-3树中删除最小节点中讨论的树根、树中和树底的情况吗？都是用上面的处理方法。
1.这个就简单了。
if (t.left == null) return null;
2.这个处理麻烦一点，需要用到旋转。我们先看一下2-3树的处理对应的红黑树。
这时候就要用到旋转，通过两次旋转，就和我们想达到的红黑树差不多了。只相差了颜色，直接看代码。
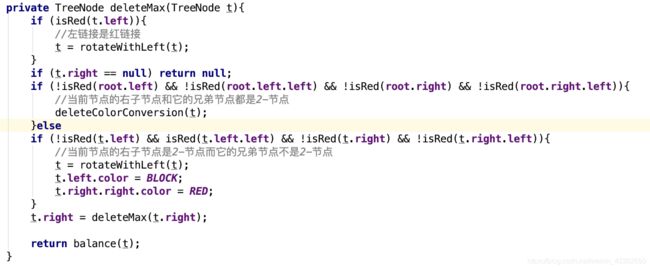
if (!isRed(t.left) && !isRed(t.left.left) && !isRed(t.right) && isRed(t.right.left)){
//当前节点的左子节点是2-节点而它的兄弟节点不是2-节点
t.right = rotateWithLeft(t.right);
t = rotateWithRight(t);
t.right.color = BLOCK;
t.left.left.color = RED;
}
3.将左子节点、当前结点和左子节点最近的兄弟节点合并成一个4-节点。我们先看一下2-3树的处理对应的红黑树。
还记得我们在插入中的颜色翻转吗？上图中就是和它相反。
if (!isRed(root.left) && !isRed(root.left.left) && !isRed(root.right) && !isRed(root.right.left)){
//当前节点的左子节点和它的兄弟节点都是2-节点
node.color = BLOCK;
node.left.color = RED;
node.right.color = RED;
}
代码
private void deleteColorConversion(TreeNode node){
node.color = BLOCK;
node.left.color = RED;
node.right.color = RED;
}
public void deleteMin(){
root = deleteMin(root);
if (!isEmpty()) root.color = BLOCK;
}
private TreeNode deleteMin(TreeNode t){
if (t.left == null) return null;
if (!isRed(root.left) && !isRed(root.left.left) && !isRed(root.right) && !isRed(root.right.left)){
//当前节点的左子节点和它的兄弟节点都是2-节点
deleteColorConversion(t);
}else
if (!isRed(t.left) && !isRed(t.left.left) && !isRed(t.right) && isRed(t.right.left)){
//当前节点的左子节点是2-节点而它的兄弟节点不是2-节点
t.right = rotateWithLeft(t.right);
t = rotateWithRight(t);
t.right.color = BLOCK;
t.left.left.color = RED;
}
t.left = deleteMin(t.left);
return balance(t);
}
看个例子,和2-3树删除最小值的例子一样的数据。
优化
我们会发现上面的代码是对应2-3树一步一步的直接实现，我们可以考虑把他优化一下。我们拿删除最小值最后的例子中的(2)(3.1)(3.2)来看代码实现的结果。
我们在看一下开始与结束。
我们可以注意到运行前和运行后’40’节点的左子树与其两棵子树的颜色都是不变的。如果在旋转前’20’节点左右子树都是红色的话，旋转后(3.2)的’30’节点左右子树叶也会是红色的。如下图所示
可以看到结果和之前是一样的，而这两种颜色的翻转我们之前也写过。这两种颜色翻转的方法我们也可以优化成一个方法
private void colorConversion(TreeNode node){
node.color = !node.color;
node.left.color = !node.left.color;
node.right.color = !node.right.color;
}
if (!isRed(t.left) && !isRed(t.left.left) && !isRed(t.right) && isRed(t.right.left)){
//当前节点的左子节点是2-节点而它的兄弟节点不是2-节点
colorConversion(t); //颜色翻转
t.right = rotateWithLeft(t.right);
t = rotateWithRight(t);
colorConversion(t); //颜色翻转
}
乍一看好像没什么区别，我们在来看一下整个方法的优化。
优化前：
我们可以注意到两个if里面都有colorConversion()方法，而它们之间都有个共同点：当前节点的左子节点不为2-节点。所以我们可以优化。
优化后的代码：
private TreeNode moveRedLeft(TreeNode t){
colorConversion(t);
if (isRed(t.right.left)){
//当前节点的左子节点是2-节点而它的兄弟节点不是2-节点
t.right = rotateWithLeft(t.right);
t = rotateWithRight(t);
colorConversion(t); //颜色翻转
}
return t;
}
public void deleteMin(){
root = deleteMin(root);
if (!isEmpty()) root.color = BLOCK;
}
private TreeNode deleteMin(TreeNode t){
if (t.left == null) return null;
if (!isRed(t.left) && !isRed(t.left.left)){ //左子节点不为2-节点
t = moveRedLeft(t);
}
t.left = deleteMin(t.left);
return balance(t);
}
优化后的删除最小值例子：
删除最大值
根据2-3树中的删除最大值，我们一直沿着右节点递归处理节点，我们需要转换的代码有下面这些：
- 当前节点右子树为空时，表示当前节点就是最小节点。处理：删除该节点。
- 当前节点的右子节点是2-节点而它的兄弟节点不是2-节点。处理：从兄弟节点借一个节点。
- 当前节点的右子节点和它的兄弟节点都是2-节点。处理：将右子节点、当前结点和右子节点最近的兄弟节点合并成一个4-节点。
删除最小值与删除最大值有个地方不一样，在删除最小值时，是一直沿着左节点递归处理，也就意味着当前节点的右节点一定是左节点的兄弟节点。在删除最大值时，是一直沿着右节点递归处理，而红链接是左链接，所以当前节点的左节点不一定是右链接的兄弟节点。所以我们遇到左链接是红链接时我们要进行一个旋转。
if (isRed(t.left)){t = rotateWithLeft(t);}
1.这个就简单了。
if (t.right == null) return null;
2.这个处理麻烦一点，需要用到旋转。我们先看一下2-3树的处理对应的红黑树。需要注意的是要注意下图中的(b)，因为要删除的节点在右边，所以我们需要给它红色右链接，这是允许的，因为这只是临时的，并且如果删除了节点50，也不存在红色右链接了。
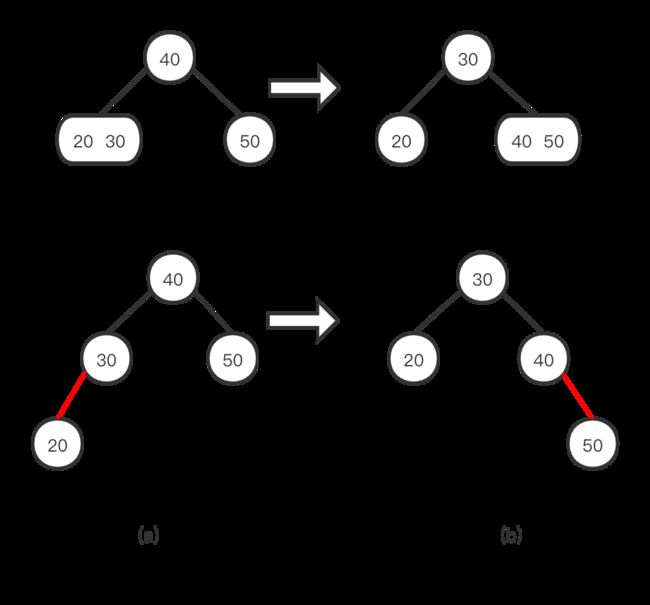
这时候就要用到旋转，通过一次旋转，就和我们想达到的红黑树差不多了。只相差了颜色，直接看代码。
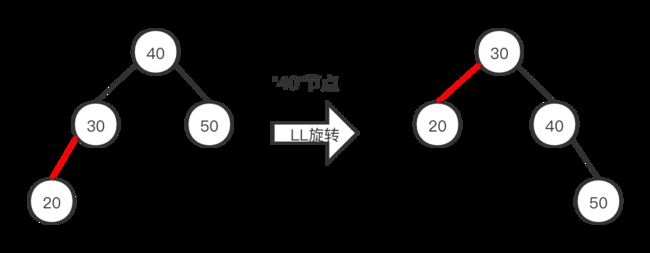
if (!isRed(t.left) && isRed(t.left.left) && !isRed(t.right) && !isRed(t.right.left)){
//当前节点的右子节点是2-节点而它的兄弟节点不是2-节点
t = rotateWithLeft(t);
t.left.color = BLOCK;
t.right.right.color = RED;
}
3.将左子节点、当前结点和左子节点最近的兄弟节点合并成一个4-节点。和删除最小的处理一样
if (!isRed(root.left) && !isRed(root.left.left) && !isRed(root.right) && !isRed(root.right.left)){
//当前节点的右子节点和它的兄弟节点都是2-节点
node.color = BLOCK;
node.left.color = RED;
node.right.color = RED;
}
代码
private void deleteColorConversion(TreeNode node){
node.color = BLOCK;
node.left.color = RED;
node.right.color = RED;
}
public void deleteMax(){
root = deleteMax(root);
if (!isEmpty()) root.color = BLOCK;
}
private TreeNode deleteMax(TreeNode t){
if (isRed(t.left)){
//左链接是红链接
t = rotateWithLeft(t);
}
if (t.right == null) return null;
if (!isRed(root.left) && !isRed(root.left.left) && !isRed(root.right) && !isRed(root.right.left)){
//当前节点的右子节点和它的兄弟节点都是2-节点
deleteColorConversion(t);
}else
if (!isRed(t.left) && isRed(t.left.left) && !isRed(t.right) && !isRed(t.right.left)){
//当前节点的右子节点是2-节点而它的兄弟节点不是2-节点
t = rotateWithLeft(t);
t.left.color = BLOCK;
t.right.right.color = RED;
}
t.right = deleteMax(t.right);
return balance(t);
}
看两个例子,第一个例子和2-3树删除最大值的例子一样的数据。第二个例子提到了左红链接的处理。
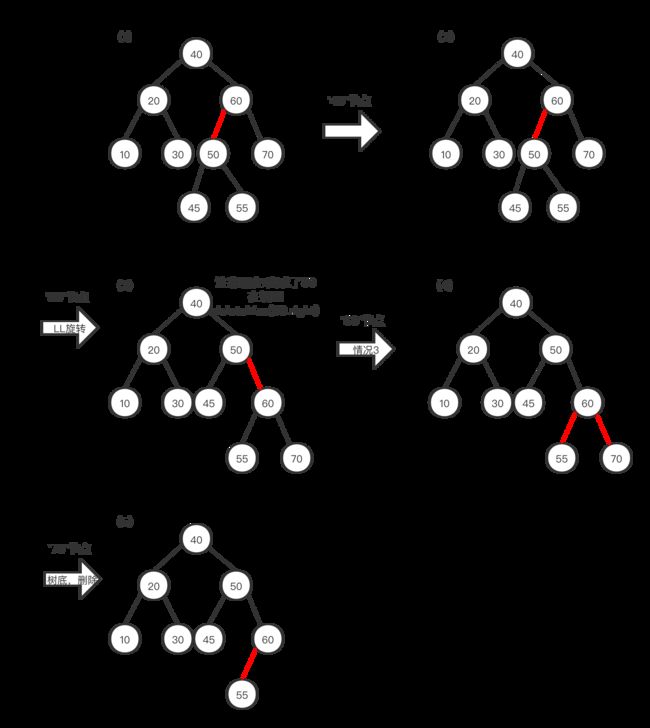
优化
和删除最小的优化思路一样。优化前：
优化后：
private TreeNode moveRedRight(TreeNode t){
colorConversion(t);
if (!isRed(t.left.left)){
//当前节点的右子节点是2-节点而它的兄弟节点不是2-节点
t = rotateWithLeft(t);
colorConversion(t);
}
return t;
}
public void deleteMax(){
root = deleteMax(root);
if (!isEmpty()) root.color = BLOCK;
}
private TreeNode deleteMax(TreeNode t){
if (isRed(t.left)){
//左链接是红链接
t = rotateWithLeft(t);
}
if (t.right == null) return null;
if (!isRed(t.right) && !isRed(t.right.left)){ //右子节点不为2-节点
t = moveRedRight(t);
}
t.right = deleteMax(t.right);
return balance(t);
}
优化后的删除最大值例子：
删除
在查找路径上进行和删除最小值或删除最大值相同的变换同样可以保证在查找过程中任意当前节点平不是2-节点。如果被查找的值在树的底部，我们可以直接删除它。如果不在，我们需要和二叉查找树中的删除一样：用其右子树的最小的值代替该节点的值，并删除那个节点(右子树的最小的值)。问题已经转化为在一棵根节点的子树中删除最小值，可以使用上面写的删除最小值的方法。
private TreeNode findMin(TreeNode t){
if (t == null) return null;
else if (t.left == null) return t;
return findMin(t.left);
}
public void delete(int data){
root = delete(root,data);
if (!isEmpty()) root.color = BLOCK;
}
private TreeNode delete(TreeNode t,int data) {
if (data < t.data) {
if (!isRed(t.left) && !isRed(t.left.left)){ //左子节点不为2-节点
t = moveRedLeft(t);
}
t.left = delete(t.left,data);
}
else
{
if (isRed(t.left)){
t = rotateWithLeft(t);
}
if (t.data == data && t.right == null){ //树底，删除
return null;
}
if (!isRed(t.right) && !isRed(t.right.left)){ //右节点不为2-节点
t = moveRedRight(t);
}
if (t.data == data){
t.data = findMin(t.right).data;
t.right = deleteMin(t.right);
}else{
t.right = delete(t.right,data);
}
}
return balance(t);
}
删除例子:
可运行代码
public class RedBlockTree{
private TreeNode root;
private static final boolean RED = true;
private static final boolean BLOCK = false;
private class TreeNode{
int data; //值
TreeNode left; //左子树
TreeNode right; //右子树
boolean color; //颜色
public TreeNode(int data,boolean color){
this.data = data;
this.color = color;
}
}
//判断节点颜色是否是红色，红色返回true，黑色或空返回false
private boolean isRed(TreeNode t){
if (t == null) return false;
return t.color == RED;
}
//判断树是否为空,为空返回true，不为空返回false
private boolean isEmpty(){
return root == null;
}
//寻找树中最小节点
private TreeNode findMin(TreeNode t){
if (t == null) return null;
else if (t.left == null) return t;
return findMin(t.left);
}
//寻找树中最大节点
private TreeNode findMax(TreeNode t){
if (t!= null){
while (t.right != null){
t = t.right;
}
}
return t;
}
//LL单旋转
private TreeNode rotateWithLeft(TreeNode k2){
TreeNode k1 = k2.left;
k2.left = k1.right;
k1.right = k2;
k1.color = k2.color;
k2.color = RED;
return k1;
}
//RR单旋转
private TreeNode rotateWithRight(TreeNode k1){
TreeNode k2 = k1.right;
k1.right = k2.left;
k2.left = k1;
k2.color = k1.color;
k1.color = RED;
return k2;
}
//翻转节点及其两个子节点的颜色
private void colorConversion(TreeNode node){
node.color = !node.color;
node.left.color = !node.left.color;
node.right.color = !node.right.color;
}
/**
* 插入数据到树中
* @param data 数据
*/
public void insert(int data){
root = insert(root,data);
root.color = BLOCK; //每次插入后根节点都要设置为黑色
}
//把data插入到以t为根的树中
private TreeNode insert(TreeNode t,int data){
if (t == null){return new TreeNode(data,RED);} //插入，和父节点用红链接相连
if (data < t.data){
t.left = insert(t.left,data);
}else if (data > t.data) {
t.right = insert(t.right,data);
}else ;
return balance(t);
}
//恢复红黑树性质
private TreeNode balance(TreeNode t){
if (isRed(t.right) && !isRed(t.left)) t = rotateWithRight(t); //有红色右链接便RR旋转
if (isRed(t.left) && isRed(t.left.left)) t= rotateWithLeft(t); //连续两条连续的红链接便LL旋转
if (isRed(t.left) && isRed(t.right)) colorConversion(t); //两个孩子都红链接便颜色转换
return t;
}
private TreeNode moveRedLeft(TreeNode t){
colorConversion(t);
if (isRed(t.right.left)){
//当前节点的左子节点是2-节点而它的兄弟节点不是2-节点
t.right = rotateWithLeft(t.right);
t = rotateWithRight(t);
colorConversion(t); //颜色翻转
}
return t;
}
public void deleteMin(){
root = deleteMin(root);
if (!isEmpty()) root.color = BLOCK;
}
private TreeNode deleteMin(TreeNode t){
if (t.left == null) return null;
if (!isRed(t.left) && !isRed(t.left.left)){ //左子节点不为2-节点
t = moveRedLeft(t);
}
t.left = deleteMin(t.left);
return balance(t);
}
private TreeNode moveRedRight(TreeNode t){
colorConversion(t);
if (isRed(t.left.left)){
//当前节点的右子节点是2-节点而它的兄弟节点不是2-节点
t = rotateWithLeft(t);
colorConversion(t);
}
return t;
}
public void deleteMax(){
root = deleteMax(root);
if (!isEmpty()) root.color = BLOCK;
}
private TreeNode deleteMax(TreeNode t){
if (isRed(t.left)){
//左链接是红链接
t = rotateWithLeft(t);
}
if (t.right == null) return null;
if (!isRed(t.right) && !isRed(t.right.left)){ //右子节点不为2-节点
t = moveRedRight(t);
}
t.right = deleteMax(t.right);
if (isRed(t.right) && !isRed(t.left)) t = rotateWithRight(t); //有红色右链接便RR旋转
if (isRed(t.left) && isRed(t.left.left)) t= rotateWithLeft(t); //连续两条连续的红链接便LL旋转
if (isRed(t.left) && isRed(t.right)) colorConversion(t); //两个孩子都红链接便颜色转换
return t;
}
public void delete(int data){
root = delete(root,data);
if (!isEmpty()) root.color = BLOCK;
}
private TreeNode delete(TreeNode t,int data) {
if (data < t.data) {
if (!isRed(t.left) && !isRed(t.left.left)){ //左子节点不为2-节点
t = moveRedLeft(t);
}
t.left = delete(t.left,data);
}
else
{
if (isRed(t.left)){
t = rotateWithLeft(t);
}
if (t.data == data && t.right == null){ //树底，删除
return null;
}
if (!isRed(t.right) && !isRed(t.right.left)){ //右节点不为2-节点
t = moveRedRight(t);
}
if (t.data == data){
t.data = findMin(t.right).data;
t.right = deleteMin(t.right);
}else{
t.right = delete(t.right,data);
}
}
return balance(t);
}
public void inorderTraversal(){
inorderTraversal(root);
}
//递归的中序遍历
private void inorderTraversal(TreeNode t){
if (t != null){
inorderTraversal(t.left);
System.out.print(t.data+" ");
inorderTraversal(t.right);
}
}
public static void main(String[] args) {
RedBlockTree tree = new RedBlockTree();
int arr[] = new int[]{9,3,5,10,11,2,1,7,8};
for (int i = 0;i < arr.length;i++){
tree.insert(arr[i]);
}
tree.inorderTraversal();
for (int i = 0;i < arr.length;i++){
tree.delete(arr[i]);
}
tree.inorderTraversal();
}
}
运行结果：
插入过程：9，3，5，10，11，2，1，7，8
删除过程：9，3，5，10，11，2，1，7，8
