浅析对称加密与非对称加密算法

1 对称加密

对称加密算法又称为传统密码算法，加密密钥和解密密钥是相同的。对称加密算法要求通信双方在开始通信前，要首先商定一个用于加密和解密的密钥。算法的安全性就依赖于这个密钥，如果这个密钥被泄露了，就意味着通信不再安全。

1.1 加密类型

根据加密方式不一样，对称加密算法又分为两种加密类型：流加密和块加密。

1.1.1 流加密

流加密：每次只对明文中的单个位或单个字节进行加密操作。优点是能够实时进行数据传输和解密，缺点是抗攻击能力比较弱。

1.1.2 块加密

块加密(也称为分组加密)：每次对明文中的一组数据进行加密操作。现在使用的分组加密算法典型的分组长度是64位，这个长度大到足以防止破译攻击，而又小到足以方便使用。块加密算法优点是抗攻击能力强，但实时性稍差。

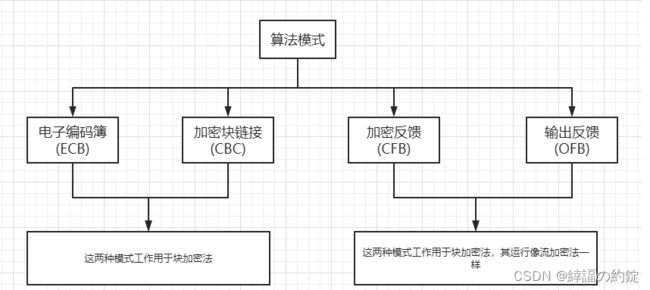
算法模式是块加密法中一系列基本算法步骤的组合。块加密法常用的加密模式：电子编码簿模式(ECB)，加密块链接模式(CBC)，加密反馈模式(CFB)，输出反馈模式(OFB)，计数器模式(CTR)。

1.1.2.1 电子编码簿模式(ECB)

电子编码簿模式是最简单的操作模式，将输入明文消息分为64位块，然后单独加密每个块，消息中所有块使用相同密钥加密。

加密步骤如下：

从加密步骤我们可以看出，ECB模式中用同一个密钥加密消息的所有块，如果原消息中重复明文块，则加密消息中的相应密文块也会重复。如果输入中一个明文块多次出现，则输出中相应的密文块也会多次出现，从而让攻击者找到漏洞进行破解。

1.1.2.2 加密块链接模式(CBC)

为了解决ECB模式中相同明文产生相同密文的问题，出现了CBC加密模式。CBC加密模式保证了即使输入中明文块相同，也能得到不同的密文块。CBC加密模式使用了反馈机制。

加密步骤如下：

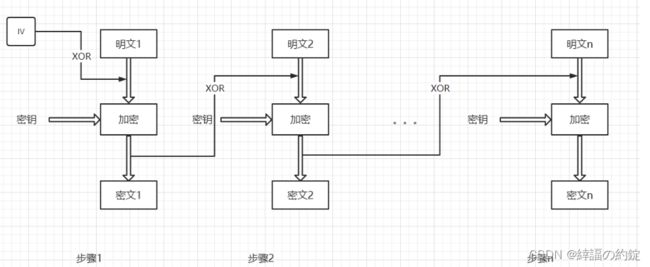
第一步接收两个输入：明文块1和一个随机文本块IV(Initialization Vector)，称为初始化向量。

初始向量没有什么特别意义，只是使每个消息唯一。初始化向量是随机生成的，可以保证明文块1即使相同也能产生不同密文块1(随机生成的初始化向量相同的概率是很小的)。

加密时第一步使用IV和明文1作异或运算，加密后得到密文1，第二步用密文1和明文2作异或运算，加密后得到密文2，后面依此类推。

初始化向量只在第一个明文块中使用，但所有明文块加密依旧使用相同密钥。

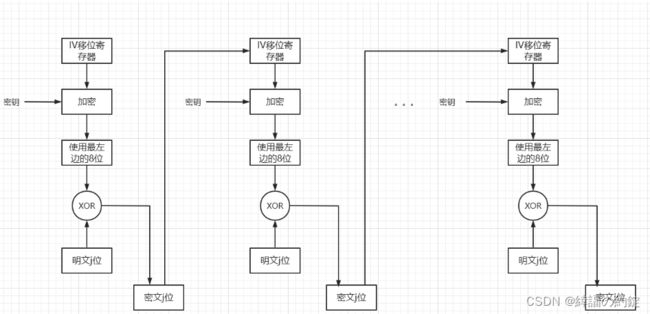
1.1.2.3 加密反馈模式(CFB)

不是所有应用程序都能处理数据块，面向字符的应用程序也需要安全性。这时要使用流加密法，可以使用加密反馈模式。

加密反馈模式中，数据用更小的单元加密(可以是8位，即一个字符的长度)，这个长度小于定义的块长(通常是64位)。假设我们一次处理j位(j通常取8)。

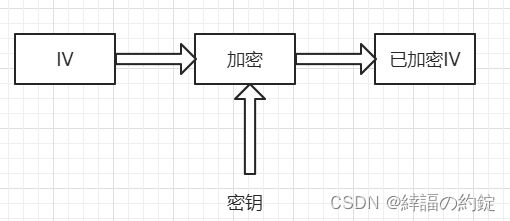
第一步：

    与CBC模式一样，加密反馈模式也使用64位的初始化向量。初始化向量放在移位寄存器中，第一步产生相应的64位初始化向量密文

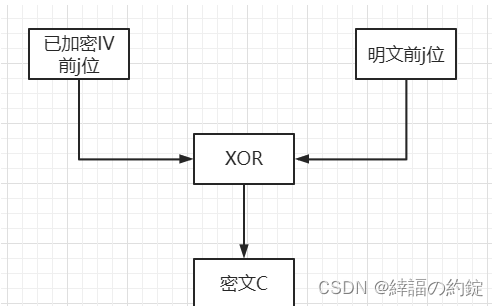
第二步：

     加密初始化向量最左边的j位与明文前j位进行异或运算，产生密文第一部分密文C。

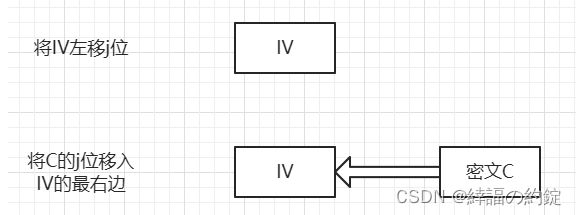
第三步：

     初始化向量的位左移j位，使移位寄存器最右边的j位为不可预测的数据，在其中填入C的内容。

第四步：

    重复1~3步，直到加密所有明文单元

总体加密过程如下：

1.1.2.4 输出反馈模式(OFB)

输出反馈模式与CFB很相似，唯一差别是，CFB中密文填入加密过程下一阶段，而在OFB中，IV加密过程的输入填入加密过程下一阶段。

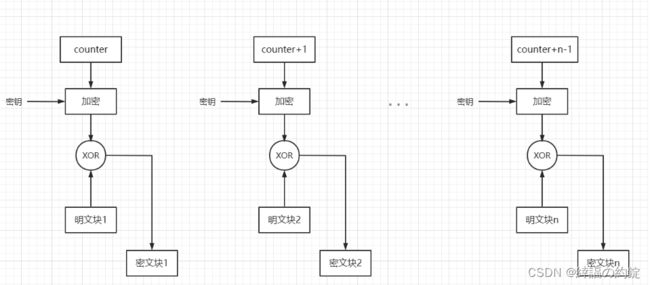
1.1.2.5 计数器模式(CTR)

计数器模式与OFB模式非常类似。它使用序号(称为计数器)作为算法的输入。每个块加密后，要填充到寄存器中，使用下一个寄存器值。通常使用一个常数作为初始计数器的值，并且每次迭代后递增(通常是增加1)。计数器块的大虚哎等于明文块的大小。

加密时，计数器加密后与明文块作XOR运算，得到密文。

1.2 对称加密算法

1.2.1 DES

全称为Data Encryption Standard，即数据加密标准。

DES是一种块加密算法，按64位块长加密数据，即把64位明文作为DES的输入，产生64位密文输出。DES工作原理:

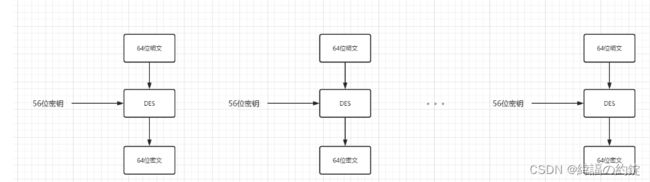
DES使用56位密钥。实际上，最初的密钥为64位，但在DES过程开始之前放弃密钥的每个第八位，从而得到56位密钥，即放弃第8、16、24、32、40、48、56、64位。

1.2.2 3DES

即三重DES，就是三次执行DES，分为两个大类

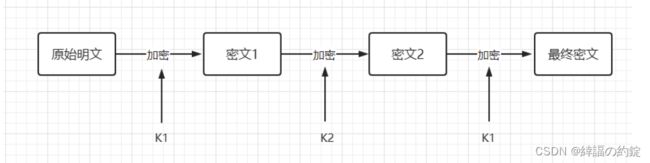
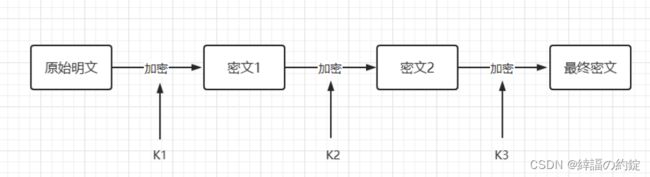
• 三个密钥的三重DES

首先用密钥K1加密明文块P，然后用密钥K2加密，最后用密钥K3加密，其中K1，K2，K3各不相同

• 两个密钥的三重DES：
  

1.2.3 AES

全称为Advanced Encryption Standard，即高级加密标准，这个标准用来替代原先的DES。

1998年6月，Rijndael算法提交给美国国家标准与技术协会(NIST)，作为AES的候选算法之一。最初有15种候选算法。2000年10月，NIST宣布AES最终选择Rijndael。

Rijndael使用的密钥和区块长度可以是32位的整数倍，以128位为下限，256位为上限。AES只选择了区块长度固定为128位，密钥长度为128，192或256位。

2006年，高级加密标准已然成为对称密钥加密中最流行的算法之一。

1.2.4 SM1

SM1 为对称加密。其加密强度与AES相当。该算法不公开，调用该算法时，需要通过加密芯片的接口进行调用。

1.2.5 SM4

SM4由我国国家密码管理局在2012年发布，常用于无线互联网加密等领域。与DES和AES算法类似，SM4算法也是一种分组加密算法。其分组长度为128位，密钥长度也为128位。

1.2.6 RC2

RC2是一种块加密算法。输入和输出块大小都是64位。而密钥是可变的，从1字节到128字节。

1.2.7 RC4

RC4是一种流加密算法。

1.2.8 RC5

RC5是一种块加密算法。块长、轮数、密钥长度都是可变的。块长可取16，32和64位。密钥长度为0~2040位。

RC5算法的特定实例记作R5-w/r/b，其中w为分组长度，r为轮数，b为密钥长度。

RC5-32/16/16 表示RC5的块长为64位(RC5一次加密2字节)，16轮和16字节(128位)密钥。

说明：

上面介绍的几种对称加密算法，只有RC4是流加密，其他都是分组加密。上面这些只是对对称加密算法进行了一个简单介绍，没有介绍这些算法的加密步骤，如果你对这些加密算法的步骤感兴趣，推荐两本书籍，可以自行去查阅：

《密码编码学与网络安全》 -[美] William Stallings 著 电子工业出版社

《密码学与网络安全》-Atul Kahate著 清华大学出版社

2 非对称加密

    非对称加密算法是现代密码学取得的最大成就之一，也是密码学近20年来能够快速发展和推广应用的主要原因之一。非对称加密算法中加密密钥和解密密钥不一样，并且解密密钥理论上很难根据加密密钥推算出来。

    非对称加密算法的加密密钥是公开的，理论上任何人都可以获得这个公开的加密密钥进行数据加密。但是，使用公开的加密密钥加密的信息只有相应的解密密钥才能解开，而这个解密密钥一般是不公开的。在非对称加密算法中，加密密钥也叫公钥，解密密钥称为私钥。

2.1 非对称加密算法

2.1.1 RSA

    RSA是被研究得最广泛的公钥算法，从提出到现在，经历了各种攻击的考验，逐渐为人们接受，普遍认为是目前最优秀的公钥方案之一。

    RSA公开密钥密码体制的原理是：根据数论，寻求两个大素数比较简单，而将它们的乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥。

    RSA算法生成密钥对以及加解密过程：

    (1) 选择两个大素数P，Q

    设P = 7，Q = 17

    (2) 计算N = P x Q

    N = 7 x 17 = 119

    (3) 选择一个公钥E，使其不是(P - 1)与(Q - 1)的因子

    (P - 1) = 6 = 2 x 3

    (Q - 1) = 16 = 2 x 2 x 2 x 2

    因此我们选的公钥E不能有因子2和3。我们取E = 5

    (4) 选择私钥D，满足：(D x E) mod (P - 1) x (Q - 1) = 1

    (D x 5) mod 6 x 16 = 1

    (D x 5) mod 96 = 1

    经计算，取D = 77

    (5) 加密时，从明文PT计算密文CT：CT =   mod N

    假设明文为10

    CT =  mod 119 = 40

    (6) 将密文CT发送给接收方

    将40发送给接收方

    (7) 解密时，从密文CT得到明文PT：PT =  mod N

     PT =  mod 119 = 10

    从上述例子可以看出，RSA算法本身很简单，关键是选择正确的密钥。

    假设B要接收A的加密消息，首先生成公钥E和私钥D，私钥D自己保留，公钥E和数字N发布出去，攻击者拿到公钥E和数字N，似乎可以通过试错法计算出私钥D。这里就到了问题的关键，从上述例子可以看出，攻击者只要从N中分解出P和Q，就可以破解私钥。我们上述例子中选择的N很小，实际N是很大的，而大素数分解是极其困难的。

2.1.2 ECC

大多数使用公钥密码学进行加密和数字签名的产品和标准都使用RSA算法。我们知道，为了保证RSA使用的安全性，最近这些年来密钥的位数一直在增加，这对使用RSA的应用是很重的负担，对进行大量安全交易的电子商务更是如此(从上面RSA加解密的例子可以推测，当要使用1024位密钥时，计算量是很大的)。

与RSA相比，ECC可以使用比RSA短得多得密钥得到相同得安全性，因此可以减少处理负荷。另一方面，虽然关于ECC的理论已经很成熟，但ECC的可信度还没有RSA高。

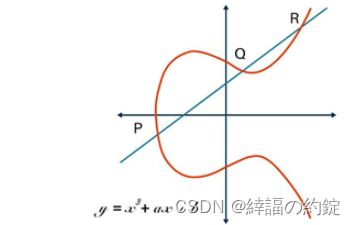
ECC全称为elliptic curve cryptography，即椭圆曲线密码学算法。安全性建立在以下数学困难问题基础之上：

椭圆曲线上的离散对数问题：

已知有限域Fp 椭圆曲线点群Ep (a,b) 及其生成元点P∈Ep (a,b)，P的阶是一个大素数。已知整数k∈Fp 和点P，求点Q=kP是容易的，但已知点P和Q求整数k则是困难的。

椭圆曲线上的两个点P和Q，k为整数，Q = kP，椭圆曲线加密的数学原理：点P称为基点，k为私钥，Q为公钥。

给定k和P，计算Q很容易。但给定P和Q，求k非常困难。

椭圆曲线方程：y = + a + b

加解密过程：

(1) 用户选定一条椭圆曲线Ep(a, b)， 并取椭圆曲线上一点作为基点P

(2) 用户A选择大数k作为私钥，并生成公钥Q = kP

(3) 用户A将Ep(a, b)，公钥Q和基点P传给B用户

(4) 用户B接受到信息后，将待传输的明文编码到Ep(a,b)上的一点M，并产生一个随机整数r。

(5) 用户B计算点C1 = M + rQ，C2 = rP

(6) 用户B将C1和C2传给A

(7) 用户A接收到信息后，计算C1 - kC2，就可以得到点M(C1 - kC2 = M + rQ - krP = M + r(Q - kP) = M)。

(8) 再对M进行解码就可以得到明文。

假设在加密过程中，有一个第三者H，H只能知道椭圆曲线 Ep(a,b)、公钥Q、基点P、密文点C(C1, C2)，而通过公钥Q、基点P求私钥k或者通过密文点C(C1, C2)、基点P求随机数r都是非常困难的，因此得以保证数据传输的安全。

密码学中，描述一条Fp上的椭圆曲线，常用到六个参量：T=(p，a，b，n，x，y)。（p 、a 、b） 用来确定一条椭圆曲线，p为素数域内点的个数，a和b是其内的两个大数；x，y为G基点的坐标，也是两个大数；n为点G基点的阶；以上六个量就可以描述一条椭圆曲线。

2.1.3 SM2

SM2算法是我国自主知识产权的商业密码算法，是ECC的一种。

ECC是基于椭圆曲线方程 y = + a + b，SM通过指定系数a，b确定了唯一的一条曲线。简单理解就是ECC选取的椭圆曲线可以有无数个，而SM2只是选取了唯一的一条椭圆曲线。

SM2椭圆曲线公钥密码算法推荐曲线参数

推荐使用素数域256位椭圆曲线。

椭圆曲线方程：y = + a + b

曲线参数：

p=FFFFFFFE FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF 00000000 FFFFFFFF FFFFFFFF

a=FFFFFFFE FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF 00000000 FFFFFFFF FFFFFFFC

b=28E9FA9E 9D9F5E34 4D5A9E4B CF6509A7 F39789F5 15AB8F92 DDBCBD41 4D940E93

n=FFFFFFFE FFFFFFFF FFFFFFFF FFFFFFFF 7203DF6B 21C6052B 53BBF409 39D54123

Gx=32C4AE2C 1F198119 5F990446 6A39C994 8FE30BBF F2660BE1 715A4589 334C74C7

Gy=BC3736A2 F4F6779C 59BDCEE3 6B692153 D0A9877C C62A4740 02DF32E5 2139F0A0

国家密码管理局已经发布了《SM2椭圆曲线公钥密码算法》公告，对SM2算法有非常详细的说明，感兴趣的读者可以自行去查阅。
国家密码管理局关于发布《SM2椭圆曲线公钥密码算法》公告（国密局公告第21号）_国家密码管理局 (oscca.gov.cn)
https://oscca.gov.cn/sca/xxgk/2010-12/17/content_1002386.shtml

3 对称加密与非对称加密技术比较

3.1 对称加密与非对称加密对比

• 对称加密

  优点：加密速度快
  缺点：密钥管理分配困难，安全性较低

• 非对称加密

  优点：安全性较高
  缺点：加密速度慢

对称加密技术加密和解密使用的都是同一个密钥，因此密钥的管理非常困难，在分发密钥的过程中，如果一方密钥被截获，那后面的通信就是不安全的。

而非对称加密技术就很好的解决了这一问题，非对称加密技术使用公钥加密，私钥加密。通信前把公钥发布出去，私钥只有自己保留，即便你的公钥被攻击者拿到，没有私钥，就无法进行解密。

那有了非对称加密技术，对称加密是不是就被淘汰了？当然不是，因为非对称加密技术加解密比较慢，不适合对大量数据的加解密。

3.2 MD5是对称加密还是非对称加密？

• 对称算法有哪些？

对称密码算法又叫传统密码算法，也就是加密密钥能够从解密密钥中推算出来，反过来也成立。在大多数对称算法中，加密解密密钥是相同的。常见的对称算法有：DES、IDEA、AES、SM1和SM4。

• 非对称算法有哪些？

非对称密钥也叫公开密钥加密,它是用两个数学相关的密钥对信息进行编码。在此系统中，其中一个密钥叫公开密钥，可随意发给期望同密钥持有者进行安全通信的人。公开密钥用于对信息加密。第二个密钥是私有密钥，属于密钥持有者，此人要仔细保存私有密钥。密钥持有者用私有密钥对收到的信息进行解密。常见的非对称算法有：RSA、ECC、SM2。

这个问题有人吐槽过，面试官竟然问MD5是对称加密还是非对称加密？其实，MD5不是加密算法，md5实际上既不是对称算法，也不是非对称加密算法。它是消息摘要（安全散列）算法。

• 对称加密和非对称加密有哪些优缺点？

  对称加密优点： 速度快，对称性加密通常在消息发送方需要加密大量数据时使用，具有算法公开、计算量小、加密速度快、加密效率高的特点。对称加密算法的优点在于加解密的高速度和使用长密钥时的解密性。

  对称加密的缺点： 密钥的管理和分发非常困难，不够安全。在数据传送前，发送方和接收方必须商定好密钥，并且双方都要保存好密钥，如果一方的密钥被泄露，那么加密信息也就不安全了，安全性得不到保证。

  非对称加密优点：安全性更高，公钥是公开的，秘钥是自己保存的，不需要将私钥给别人。

  非对称加密缺点：加密和解密花费时间长、速度慢，只适合对少量数据进行加密

• MD5优缺点

  MD5的优点：计算速度快，加密速度快，不需要密钥；可以检查文件的完整性，一旦文件被更改，MD5值会改变；防止被篡改，传输中一旦被篡改，计算出的MD5值也会改变；防止看到明文，公司存放密码存放的是MD5值。

  MD5的缺点：作为散列算法，经过证实，仍然会存在两种不同数据会发生碰撞；MD5的安全性。将用户的密码直接MD5后存储在数据库中是不安全的。很多人使用的密码是常见的组合，威胁者将这些密码的常见组合进行单向哈希，得到一个摘要组合，然后与数据库中的摘要进行比对即可获得对应的密码。

综上所述，md5是消息摘要算法，既不是对称算法也不是非对称算法。大部分情况下使用对称加密具有不错的安全性，如果需要分布式进行密钥分发，那么就考虑使用非对称加密；如果不需要可逆计算，则考虑散列算法（md5）。

参考资料：https://www.eolink.com/news/post/28567.html

4 实践部分

接下来我们就实际操作一下，先介绍一下开源库openssl。

OpenSSL 是一个开源且功能强大的包含丰富的密码算法和 SSL/TLS 协议的库，主要包括的密码算法、常用的密钥和证书封装管理功能及 SSL 协议，并提供了多用途的命令行工具。使用 c 语言编写，跨平台性能好，支持 Linux、Windows、BDS、Mac、VMS 等平台。

    Openssl由3部分组成

            - The Crypto library(密码学算法库)

            - The SSL library(SSL/TLS协议库)         

            - Command line tool(命令行工具) 

ubuntu下安装命令：

sudo apt-get install openssl

sudo apt-get install libssl-dev

安装后就可以直接使用openssl命令行工具。

windows可以通过源码安装或者直接下载安装包安装

安装包下载地址：
Win32/Win64 OpenSSL Installer for Windows - Shining Light Productions (slproweb.com)
http://slproweb.com/products/Win32OpenSSL.html

4.1 对称加密工具

enc是openssl提供的一个对称加解密命令行工具。安装openssl后，执行命令openssl enc -list，可以看到enc支持的所有对称加密算法

lng@ubuntu:~$ openssl enc -list
Supported ciphers:
-aes-128-cbc               -aes-128-cfb               -aes-128-cfb1             
-aes-128-cfb8              -aes-128-ctr               -aes-128-ecb              
-aes-128-ofb               -aes-192-cbc               -aes-192-cfb              
-aes-192-cfb1              -aes-192-cfb8              -aes-192-ctr              
-aes-192-ecb               -aes-192-ofb               -aes-256-cbc              
-aes-256-cfb               -aes-256-cfb1              -aes-256-cfb8             
-aes-256-ctr               -aes-256-ecb               -aes-256-ofb              
-aes128                    -aes128-wrap               -aes192                   
-aes192-wrap               -aes256                    -aes256-wrap              
-aria-128-cbc              -aria-128-cfb              -aria-128-cfb1            
-aria-128-cfb8             -aria-128-ctr              -aria-128-ecb             
-aria-128-ofb              -aria-192-cbc              -aria-192-cfb             
-aria-192-cfb1             -aria-192-cfb8             -aria-192-ctr             
-aria-192-ecb              -aria-192-ofb              -aria-256-cbc             
-aria-256-cfb              -aria-256-cfb1             -aria-256-cfb8            
-aria-256-ctr              -aria-256-ecb              -aria-256-ofb             
-aria128                   -aria192                   -aria256                  
-bf                        -bf-cbc                    -bf-cfb                   
-bf-ecb                    -bf-ofb                    -blowfish                 
-camellia-128-cbc          -camellia-128-cfb          -camellia-128-cfb1        
-camellia-128-cfb8         -camellia-128-ctr          -camellia-128-ecb         
-camellia-128-ofb          -camellia-192-cbc          -camellia-192-cfb         
-camellia-192-cfb1         -camellia-192-cfb8         -camellia-192-ctr         
-camellia-192-ecb          -camellia-192-ofb          -camellia-256-cbc         
-camellia-256-cfb          -camellia-256-cfb1         -camellia-256-cfb8        
-camellia-256-ctr          -camellia-256-ecb          -camellia-256-ofb         
-camellia128               -camellia192               -camellia256              
-cast                      -cast-cbc                  -cast5-cbc                
-cast5-cfb                 -cast5-ecb                 -cast5-ofb                
-chacha20                  -des                       -des-cbc                  
-des-cfb                   -des-cfb1                  -des-cfb8                 
-des-ecb                   -des-ede                   -des-ede-cbc              
-des-ede-cfb               -des-ede-ecb               -des-ede-ofb              
-des-ede3                  -des-ede3-cbc              -des-ede3-cfb             
-des-ede3-cfb1             -des-ede3-cfb8             -des-ede3-ecb             
-des-ede3-ofb              -des-ofb                   -des3                     
-des3-wrap                 -desx                      -desx-cbc                 
-id-aes128-wrap            -id-aes128-wrap-pad        -id-aes192-wrap           
-id-aes192-wrap-pad        -id-aes256-wrap            -id-aes256-wrap-pad       
-id-smime-alg-CMS3DESwrap  -rc2                       -rc2-128                  
-rc2-40                    -rc2-40-cbc                -rc2-64                   
-rc2-64-cbc                -rc2-cbc                   -rc2-cfb                  
-rc2-ecb                   -rc2-ofb                   -rc4                      
-rc4-40                    -seed                      -seed-cbc                 
-seed-cfb                  -seed-ecb                  -seed-ofb                 
-sm4                       -sm4-cbc                   -sm4-cfb                  
-sm4-ctr                   -sm4-ecb                   -sm4-ofb

enc完整命令:

openssl enc -ciphername [-in filename] [-out filename] [-pass arg] [-e ] [-d ] [-a ] [-A] [-k password ] [-kfile filename] [-K key] [-iv IV] [-p] [-P] [-bufsize number] [-nopad] [-debug]

-ciphername：对称算法名称(就是上面执行openssl enc -list命令后展示的那些)

-in filename：输入文件，默认为标准输入。

-out filename：输出文件，默认为标准输出。

-pass arg：输入文件如果有密码保护，指定密码来源。

-e：进行加密操作，默认操作。

-d：进行解密操作。

-a：当进行加解密时，它只对数据进行运算，有时需要进行base64转换。设置此选项后，加密结果进行base64编码；解密前先进行base64解码。

-A：默认情况下，base64编码结果在文件中是多行的。如果要将生成的结果在文件中只有一行，需设置此选项；解密时，必须采用同样的设置，否则读取数据时会出错。

-k password：指定加密口令，不设置此项时，程序会提示用户输入口令。

-kfile filename：指定口令存放的文件。

-K key：密钥，为16进制。

-iv IV：初始化向量，为16进制。

-p：打印出使用的salt、口令以及初始化向量IV。

-P：打印使用的salt、口令以及IV，不做加密和解密操作。

-bufsize number：设置I/O操作的缓冲区大小，因为一个文件可能很大，每次读取的数据是有限的。

-debug：打印调试信息。

4.1.1 AES加解密

加密命令:

openssl enc -aes-128-cbc -in in.txt -out out.txt -a -K 001122334455BBCCDDEEFF0011223344 -iv 0123456789ABCDEF0123456789ABCDEF

我们选择的密钥长度为128位，从上面列表可以知道，密钥长度可以选取128位，192位，256位。选择的加密模式为cbc，加密模式可以选取ecb，cbc，cfb，ofb，ctr。加密模式是什么意思在上面已经将的很清楚了。

演示:

lng@ubuntu:~/CSDN/enc$ cat in.txt 
hello word
lng@ubuntu:~/CSDN/enc$ openssl enc -aes-128-cbc -in in.txt -out out.txt -a -K 001122334455BBCCDDEEFF0011223344 -iv 0123456789ABCDEF0123456789ABCDEF
lng@ubuntu:~/CSDN/enc$ ls
in.txt  out.txt
lng@ubuntu:~/CSDN/enc$ cat out.txt 
Bqbu9rk0uOXRgahyZWW7tA==
lng@ubuntu:~/CSDN/enc$ 

解密命令:

openssl enc -aes-128-cbc -in out.txt -out inin.txt -d -a -K 001122334455BBCCDDEEFF0011223344 -iv 0123456789ABCDEF0123456789ABCDEF

演示：

lng@ubuntu:~/CSDN/enc$ openssl enc -aes-128-cbc -in out.txt -out inin.txt -d -a -K 001122334455BBCCDDEEFF0011223344 -iv 0123456789ABCDEF0123456789ABCDEF
lng@ubuntu:~/CSDN/enc$ ls
inin.txt  in.txt  out.txt
lng@ubuntu:~/CSDN/enc$ cat inin.txt 
hello word
lng@ubuntu:~/CSDN/enc$ 

注意：如果你要阅读密文，要指定参数-a进行base64编码，否则密文是二进制文件，解密时也要指定-a参数，先进行base64解码，再进行解密。可以选择不同的密钥长度和不同的加密模式，看看密文有什么不同，我这里就不演示了。

• 默认是加密操作，加密时可以不指定参数，但解密时我们要指定参数-d

• ecb模式是没有初始化向量的，所以ecb模式我们不用指定-iv参数

4.1.2 DES加解密

des密钥长度是固定的，为64位，所以我们只需要选择加密模式。

lng@ubuntu:~/CSDN/enc$ cat  in.txt 
hello word
lng@ubuntu:~/CSDN/enc$ openssl enc -des-ecb -K 0123456789AAAAAA -in in.txt -out out.txt -a
lng@ubuntu:~/CSDN/enc$ ls
in.txt  out.txt
lng@ubuntu:~/CSDN/enc$ cat out.txt 
munBF17bqEeZ28tiddZVxg==
lng@ubuntu:~/CSDN/enc$ openssl enc -des-ecb -d -K 0123456789AAAAAA -in out.txt -out inin.txt -a
lng@ubuntu:~/CSDN/enc$ ls
inin.txt  in.txt  out.txt
lng@ubuntu:~/CSDN/enc$ cat inin.txt 
hello word
lng@ubuntu:~/CSDN/enc$ 

4.2 非对称加密工具

4.2.1 RSA加密

这里介绍下openssl命令行工具的两个命令

genrsa 生成rsa密钥

rsa 用于处理rsa密钥，格式转换和打印信息

生成私钥

# private.key 为私钥文件，其中包含公钥和私钥，1024为密钥长度
openssl genrsa -out private.key 1024

导出公钥

# 从私钥文件中导出公钥
openssl rsa -in private.key -pubout -out public.key

使用公钥加密

openssl rsautl -encrypt -pubin -inkey public.key -in in.txt -out out.txt

使用私钥解密

openssl rsautl -decrypt -inkey private.key -in out.txt -out inin.txt

4.2.2 ECC加密

ecparam 椭圆曲线密钥参数生成及操作

ec 椭圆曲线密钥处理工具

查看支持的椭圆曲线

openssl ecparam -list_curves

可以看到支持的所有椭圆曲线，最前面的就是曲线名称。

  secp112r1 : SECG/WTLS curve over a 112 bit prime field
  secp112r2 : SECG curve over a 112 bit prime field
  secp128r1 : SECG curve over a 128 bit prime field
  secp128r2 : SECG curve over a 128 bit prime field
  secp160k1 : SECG curve over a 160 bit prime field
  secp160r1 : SECG curve over a 160 bit prime field
  secp160r2 : SECG/WTLS curve over a 160 bit prime field
  secp192k1 : SECG curve over a 192 bit prime field
  secp224k1 : SECG curve over a 224 bit prime field
  secp224r1 : NIST/SECG curve over a 224 bit prime field
  secp256k1 : SECG curve over a 256 bit prime field
  secp384r1 : NIST/SECG curve over a 384 bit prime field
  secp521r1 : NIST/SECG curve over a 521 bit prime field
  prime192v1: NIST/X9.62/SECG curve over a 192 bit prime field
  prime192v2: X9.62 curve over a 192 bit prime field
  prime192v3: X9.62 curve over a 192 bit prime field
  prime239v1: X9.62 curve over a 239 bit prime field
  prime239v2: X9.62 curve over a 239 bit prime field
  prime239v3: X9.62 curve over a 239 bit prime field
  prime256v1: X9.62/SECG curve over a 256 bit prime field
  sect113r1 : SECG curve over a 113 bit binary field
  sect113r2 : SECG curve over a 113 bit binary field
  sect131r1 : SECG/WTLS curve over a 131 bit binary field
  sect131r2 : SECG curve over a 131 bit binary field
  sect163k1 : NIST/SECG/WTLS curve over a 163 bit binary field
  sect163r1 : SECG curve over a 163 bit binary field
  sect163r2 : NIST/SECG curve over a 163 bit binary field
  sect193r1 : SECG curve over a 193 bit binary field
  sect193r2 : SECG curve over a 193 bit binary field
  sect233k1 : NIST/SECG/WTLS curve over a 233 bit binary field
  sect233r1 : NIST/SECG/WTLS curve over a 233 bit binary field
  sect239k1 : SECG curve over a 239 bit binary field
  sect283k1 : NIST/SECG curve over a 283 bit binary field
  sect283r1 : NIST/SECG curve over a 283 bit binary field
  sect409k1 : NIST/SECG curve over a 409 bit binary field
  sect409r1 : NIST/SECG curve over a 409 bit binary field
  sect571k1 : NIST/SECG curve over a 571 bit binary field
  sect571r1 : NIST/SECG curve over a 571 bit binary field
  c2pnb163v1: X9.62 curve over a 163 bit binary field
  c2pnb163v2: X9.62 curve over a 163 bit binary field
  c2pnb163v3: X9.62 curve over a 163 bit binary field
  c2pnb176v1: X9.62 curve over a 176 bit binary field
  c2tnb191v1: X9.62 curve over a 191 bit binary field
  c2tnb191v2: X9.62 curve over a 191 bit binary field
  c2tnb191v3: X9.62 curve over a 191 bit binary field
  c2pnb208w1: X9.62 curve over a 208 bit binary field
  c2tnb239v1: X9.62 curve over a 239 bit binary field
  c2tnb239v2: X9.62 curve over a 239 bit binary field
  c2tnb239v3: X9.62 curve over a 239 bit binary field
  c2pnb272w1: X9.62 curve over a 272 bit binary field
  c2pnb304w1: X9.62 curve over a 304 bit binary field
  c2tnb359v1: X9.62 curve over a 359 bit binary field
  c2pnb368w1: X9.62 curve over a 368 bit binary field
  c2tnb431r1: X9.62 curve over a 431 bit binary field
  wap-wsg-idm-ecid-wtls1: WTLS curve over a 113 bit binary field
  wap-wsg-idm-ecid-wtls3: NIST/SECG/WTLS curve over a 163 bit binary field
  wap-wsg-idm-ecid-wtls4: SECG curve over a 113 bit binary field
  wap-wsg-idm-ecid-wtls5: X9.62 curve over a 163 bit binary field
  wap-wsg-idm-ecid-wtls6: SECG/WTLS curve over a 112 bit prime field
  wap-wsg-idm-ecid-wtls7: SECG/WTLS curve over a 160 bit prime field
  wap-wsg-idm-ecid-wtls8: WTLS curve over a 112 bit prime field
  wap-wsg-idm-ecid-wtls9: WTLS curve over a 160 bit prime field
  wap-wsg-idm-ecid-wtls10: NIST/SECG/WTLS curve over a 233 bit binary field
  wap-wsg-idm-ecid-wtls11: NIST/SECG/WTLS curve over a 233 bit binary field
  wap-wsg-idm-ecid-wtls12: WTLS curve over a 224 bit prime field
  Oakley-EC2N-3: 
	IPSec/IKE/Oakley curve #3 over a 155 bit binary field.
	Not suitable for ECDSA.
	Questionable extension field!
  Oakley-EC2N-4: 
	IPSec/IKE/Oakley curve #4 over a 185 bit binary field.
	Not suitable for ECDSA.
	Questionable extension field!
  brainpoolP160r1: RFC 5639 curve over a 160 bit prime field
  brainpoolP160t1: RFC 5639 curve over a 160 bit prime field
  brainpoolP192r1: RFC 5639 curve over a 192 bit prime field
  brainpoolP192t1: RFC 5639 curve over a 192 bit prime field
  brainpoolP224r1: RFC 5639 curve over a 224 bit prime field
  brainpoolP224t1: RFC 5639 curve over a 224 bit prime field
  brainpoolP256r1: RFC 5639 curve over a 256 bit prime field
  brainpoolP256t1: RFC 5639 curve over a 256 bit prime field
  brainpoolP320r1: RFC 5639 curve over a 320 bit prime field
  brainpoolP320t1: RFC 5639 curve over a 320 bit prime field
  brainpoolP384r1: RFC 5639 curve over a 384 bit prime field
  brainpoolP384t1: RFC 5639 curve over a 384 bit prime field
  brainpoolP512r1: RFC 5639 curve over a 512 bit prime field
  brainpoolP512t1: RFC 5639 curve over a 512 bit prime field
  SM2       : SM2 curve over a 256 bit prime field

生成参数文件，选择一条曲线生成参数文件

openssl ecparam -name secp256k1 -out secp256k1.pem

显示参数文件参数

openssl ecparam -in secp256k1.pem -text -param_enc explicit -noout

使用参数文件生成私钥

openssl ecparam -in secp256k1.pem -genkey -out secp256k1-key.key

从私钥中导出公钥

openssl ec -in secp256k1-key.key -pubout -out public.key

参考资料：
《密码编码学与网络安全》 -[美] William Stallings 著 电子工业出版社
《密码学与网络安全》-Atul Kahate著 清华大学出版社

注：
版权声明：本文为CSDN博主「大草原的小灰灰」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/new9232/article/details/122670049

写博客是为了记住自己容易忘记的东西，另外也是对自己工作的总结，希望尽自己的努力，做到更好，大家一起努力进步！

如果有什么问题，欢迎大家一起探讨，代码如有问题，欢迎各位大神指正！

给自己的梦想添加一双翅膀，让它可以在天空中自由自在的飞翔！