CUDA学习(十二):矩阵乘法
博主CUDA学习系列汇总传送门(持续更新):编程语言|CUDA入门
文章目录
-
- 一、CPU下一般矩阵乘法
- 二、CPU下循环交换矩阵乘法
- 三、CPU下转置矩阵乘法
本文章为 《 GPU编程与优化 大众高性能计算》的读书笔记,例子也都取自书中教程。
矩阵乘法的运算量和数据量的关系不再是线性关系,对应的运算量为 O ( n 3 ) O(n^3) O(n3)。
矩阵乘法的数学表达式如下:
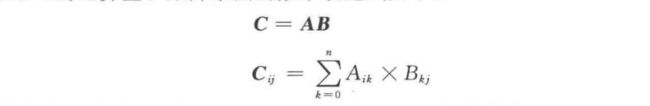 本质上看,矩阵陈发是向量内积的集合, C C C矩阵的每一个元素都是 A A A矩阵一行和 B B B矩阵一列的向量内积。
本质上看,矩阵陈发是向量内积的集合, C C C矩阵的每一个元素都是 A A A矩阵一行和 B B B矩阵一列的向量内积。
在C语言中,数据是按行存储的,所以 B B B矩阵的访存不连续,导致catch命中失效。
一、CPU下一般矩阵乘法
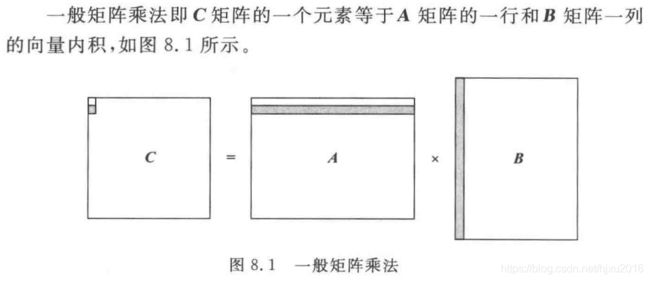 其中 A A A矩阵大小为 m m m行 l l l列, B B B矩阵的大小为 l l l行 n n n列,相乘后得到 C C C矩阵大小为 m m m行 n n n列。
其中 A A A矩阵大小为 m m m行 l l l列, B B B矩阵的大小为 l l l行 n n n列,相乘后得到 C C C矩阵大小为 m m m行 n n n列。
这种方法的思路是一次完成 C C C矩阵中一个元素的计算,然后通过循环迭代的方法完成 C C C矩阵所有元素的运算。
平均耗时为 4458ms
#include 二、CPU下循环交换矩阵乘法
 本例子平均耗时 2479ms;
本例子平均耗时 2479ms;
注意,因为这种方法没有采用中间变量,所以当矩阵数字很大时,超出float能表示的范围会导致结果不正确。
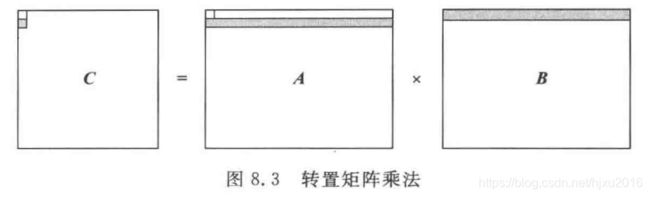
#include 三、CPU下转置矩阵乘法
为了解决访存不连续,无法向量化的问题,除了内部两层循环交换的方法,还可以采用转置矩阵的方法。
即对 B B B矩阵转置,转置后,就编程 A A A矩阵的一行和 B B B矩阵的一行做向量内积运算。因为 B B B矩阵是按行访问的,因此具有cache命中率、数据连续访存、可向量化等有点。
#include 未完待续。。。