【数据挖掘 | 关联性分析】万字长文详解关联性分析，详解Apriori算法为例，确定不来看看？

‍♂️ 个人主页: @AI_magician
主页地址： 作者简介：CSDN内容合伙人，全栈领域优质创作者。
‍景愿：旨在于能和更多的热爱计算机的伙伴一起成长！！‍
‍♂️声明：本人目前大学就读于大二，研究兴趣方向人工智能&硬件（虽然硬件还没开始玩，但一直很感兴趣！希望大佬带带）

【数据挖掘 | 关联性分析】万字长文详解关联性分析，详解Apriori算法为例，确定不来看看？ 作者： 计算机魔术师 版本： 1.0 （ 2023.10.27 ）

---

摘要： 本系列旨在普及那些深度学习路上必经的核心概念，文章内容都是博主用心学习收集所写，欢迎大家三联支持！本系列会一直更新，核心概念系列会一直更新！欢迎大家订阅

该文章收录专栏
[✨— 《深入解析机器学习：从原理到应用的全面指南》 —✨]

@toc

关联性分析

数据挖掘中的关联分析是一种用于发现数据集中不同项之间的关联关系的方法。关联分析通常用于在大规模数据集中发现频繁项集和关联规则。总的来说，关联规则通过量化的数字决定某物品甲对物品乙的出现有多大的影响。该模式属于描述性模式，属于**无监督学习**的方法

下面是几种常见的关联分析方法及其详细解释：

1. 频繁项集挖掘（Frequent Itemset Mining）：频繁项集是指在数据集中同时出现的项的集合。频繁项集挖掘的目标是找到在数据集中出现频率高于预定义阈值的项集。常用的频繁项集挖掘算法包括Apriori算法和FP-Growth算法。

2. 关联规则挖掘（Association Rule Mining）：关联规则是指项集之间的条件关系，例如"A->B"表示项集A出现时，项集B也可能出现。关联规则挖掘的目标是从频繁项集中找到具有一定置信度的关联规则。关联规则通常使用支持度和置信度来衡量规则的重要性。常用的关联规则挖掘算法包括Apriori算法和FP-Growth算法。

3. 序列模式挖掘（Sequential Pattern Mining）：序列模式是指在时间序列数据中出现的一系列项的序列。序列模式挖掘的目标是发现在时间序列数据中频繁出现的序列模式。序列模式挖掘算法需要考虑项的出现顺序和时间跨度，常用的算法包括GSP（Generalized Sequential Pattern）算法和PrefixSpan算法。

4. 关联网络分析（Association Network Analysis）：关联网络分析是通过构建关联网络来分析数据集中的关联关系。关联网络由节点和边组成，其中节点代表项集，边代表项集之间的关联关系。关联网络分析可以帮助识别关键节点和关联子图，从而揭示数据集的结构和关联模式。

5. 多层次关联分析（Multilevel Association Analysis）：多层次关联分析是一种用于发现数据集中多个层次的关联关系的方法。它可以在不同的抽象层次上进行关联分析，从而揭示数据集中的多个关联模式。多层次关联分析可以通过层次划分、多层次关联规则和多层次关联网络来实现。

这些关联分析方法在数据挖掘中被广泛应用，可以帮助发现数据集中的隐含关系和模式，提供有价值的洞察和决策支持。根据具体的应用场景和数据特点，选择适合的关联分析方法进行数据挖掘分析。

下面是常用的关联规则算法的详细解释、优缺点以及以Markdown表格格式给出的总结：

算法名称	算法描述	优缺点
Apriori算法	基于频繁项集的挖掘算法。通过迭代生成候选项集，并利用候选项集的频率计算支持度，从而找到频繁项集。然后，使用频繁项集生成关联规则，并计算置信度。	优点：简单易懂，易于实现。 缺点：需要多次扫描数据集，计算复杂度较高；随着项集的增长，候选项集的数量呈指数级增加，导致算法效率较低。
FP-Growth算法	使用频繁模式树（FP-Tree）的挖掘算法。首先构建FP-Tree，然后通过递归将FP-Tree划分为条件模式基，从而找到频繁项集。最后，使用频繁项集生成关联规则，并计算置信度。	优点：相对于Apriori算法，减少了多次扫描数据集的开销，提高了算法效率；对于大规模数据集，效果更好。 缺点：构建FP-Tree的过程可能需要占用较大的内存空间；在某些情况下，FP-Growth算法的性能可能略差于Apriori算法。
ECLAT算法	基于垂直数据格式的挖掘算法。将事务数据转换为垂直格式，其中每个项与对应的事务列表相关联。通过递归搜索和交集操作，找到频繁项集。然后，使用频繁项集生成关联规则，并计算置信度。	优点：相对于Apriori算法，减少了候选项集的生成和扫描开销，提高了算法效率；对于稠密数据集，效果更好。 缺点：在稀疏数据集中，性能可能不如Apriori算法和FP-Growth算法。
FPMax算法	一种寻找最大频繁项集的算法。与FP-Growth算法类似，但不生成所有频繁项集。首先找到频繁项集，然后通过计算每个频繁项集的闭包，将非最大频繁项集排除。	优点：相对于FP-Growth算法，减少了频繁项集的生成和存储开销，提高了算法效率；仅保留最大频繁项集，减少了关联规则的数量，提高了结果的可解释性。 缺点：对于频繁项集较多或具有很大差异的数据集，性能可能不如FP-Growth算法。
Direct Hashing算法	一种基于哈希表的挖掘算法。通过构建候选项集哈希表和事务哈希表，生成候选项集，并计算支持度。然后，通过哈希表的操作，找到频繁项集。最后，使用频繁项集生成关联规则，并计算置信度。	优点：对于稠密数据集和小规模数据集，效果较好；在一些特定情况下，算法性能可能优于其他算法。 缺点：对于稀疏数据集和大规模数据集，性能可能不如其他算法；哈希表的构建和操作可能占用于关联规则挖掘的常见算法有：
灰色关联分析算法	灰色关联分析算法是一种用于处理灰色系统的分析方法。它通过将不确定的数据序列转化为确定的关联度序列，从而揭示因素之间的关联性和影响程度。算法的基本思想是通过计算序列数据的关联度，来评估不同因素对于系统演化的影响程度。灰色关联分析算法主要包括数据序列预处理、关联度计算和排序三个步骤。在关联度计算中，常用的方法有灰色关联度、绝对关联度和相对关联度等。灰色关联分析算法可以广泛应用于各种领域，如经济、环境、工程等。	优点： - 能够处理不完整、不确定和不精确的数据，适用于灰色系统建模。 - 相对简单易用，计算速度较快。 - 能够揭示因素之间的关联性和影响程度，有助于分析决策和预测。 缺点： - 对于数据的选择和预处理要求较高，需要根据具体问题进行合理的处理。 - 算法的结果受到数据质量和特征选择的影响，可能存在一定的主观性。 - 算法基于关联度的计算，对于高维数据或者复杂关系的分析可能存在局限性。

以上方法中实现较好的为Apriori算法，以及灰色关联分析算法。

Apriori 算法

Apriori算法的名称来源于拉丁语词汇"priori"，意为"在之前"或"在前面"。这个名称反映了Apriori算法的基本思想，即通过先前的频繁项集来生成更大的候选项集，并通过剪枝操作来减少搜索空间。

该算法最早由R.Agrawal和R.Srikant在1994年的论文《Fast Algorithms for Mining Association Rules》中提出。在该论文中，作者提出了一种基于频繁项集的关联规则挖掘方法，其中的核心思想就是利用"先验知识"（prior knowledge）来加速挖掘过程。

下面详细介绍Apriori算法的步骤和数学推导：

1. 数据预处理：首先，需要对数据进行预处理，确保数据集的格式适用于Apriori算法。通常，数据集采用事务表示，每个事务由若干项组成，项可以是商品、产品或其他类型的数据。

2. 构建候选项集：根据预处理的数据集，首先生成所有可能的单个项集作为候选项集。对于大规模数据集，可以使用特殊的数据结构（如FP树）来加速候选项集的生成。

3. 计算候选项集的支持度：遍历数据集，统计每个候选项集在数据集中出现的次数，即候选项集的支持度。支持度表示项集在数据集中出现的频率。

4. 剪枝操作：根据设定的最小支持度阈值，将支持度低于阈值的候选项集剪枝，去除非频繁项集。这样可以减少后续步骤中的搜索空间。

5. 组合生成更大的候选项集：从频繁项集中生成新的候选项集。对于频繁项集Lk-1，将其两两组合生成候选项集Ck，其中k表示项集的大小。

6. 重复步骤3-5，直到无法生成更多的候选项集。

7. 生成关联规则：对于每个频繁项集，生成关联规则。关联规则的生成可以通过逐个项集的方式，或者通过递归方式生成更多的规则。

8. 计算置信度：计算每个关联规则的置信度。置信度表示规则的可信程度，即前项和后项同时出现的概率。

9. 根据设定的最小置信度阈值，筛选出满足置信度要求的关联规则。

10. 返回满足条件的关联规则作为挖掘结果。

    我们举一个实际例子来更好理解

    假设我们有以下数据集：

    数据集：
    Transaction 1: {牛奶, 面包, 蛋}
    Transaction 2: {面包, 小麦, 橙汁}
    Transaction 3: {牛奶, 小麦, 蛋}
    Transaction 4: {面包, 牛奶, 小麦, 蛋}
    Transaction 5: {面包, 牛奶, 橙汁}

    现在我们将按照Apriori算法的步骤进行求解：

    步骤1：准备数据集
    数据集已经给定如上所示。

    步骤2：确定最小支持度阈值
    假设我们选择最小支持度阈值为2，表示一个项目集在数据集中至少出现2次才被认为是频繁项集。

    步骤3：生成候选项集
    初始候选项集包含单个项目，即C1 = {牛奶, 面包, 蛋, 小麦, 橙汁}。

    步骤4：计算候选项集的支持度
    计算候选项集的支持度，统计每个候选项集在数据集中的出现次数。

    C1的支持度计数：
    牛奶: 2
    面包: 4
    蛋: 2
    小麦: 3
    橙汁: 2

    步骤5：筛选频繁项集
    根据最小支持度阈值，筛选出支持度大于或等于2的项集作为频繁项集。

    L1 = {面包, 小麦}

    步骤6：生成关联规则
    对于频繁项集L1，生成其所有可能的关联规则。

    关联规则集R1 = {面包 -> 小麦, 小麦 -> 面包}

    步骤7：计算关联规则的置信度
    计算关联规则的置信度，即计算规则的条件发生时，结论也发生的概率。

    置信度计算：
    面包 -> 小麦：支持度(面包, 小麦) / 支持度(面包) = 3/4 = 0.75
    小麦 -> 面包：支持度(面包, 小麦) / 支持度(小麦) = 3/3 = 1.00

    步骤8：筛选强关联规则
    根据设定的最小置信度阈值，筛选出置信度大于或等于0.7的关联规则作为强关联规则。

    强关联规则集R1 = {面包 -> 小麦, 小麦 -> 面包}

    通过以上步骤，我们完成了Apriori算法对给定数据集的求解。不过还有的是这里只展示两个

    此外得到的频繁项集中还有以下各项指标

    • lift（提升度）是关联规则分析中的一个度量，用于衡量两个事件之间的关联程度。它表示两个事件同时发生的概率与它们各自独立发生的概率之比。当提升度大于1时，表示两个事件之间存在正向关联，即它们的出现是相互促进的。当提升度等于1时，表示两个事件之间不存在关联。当提升度小于1时，表示两个事件之间存在负向关联，即它们的出现是相互抑制的。

    • leverage（杠杆率）是关联规则分析中的另一个度量，用于衡量两个事件之间的关联程度。它表示两个事件同时发生的概率与在假设它们是独立事件的情况下预期同时发生的概率之间的差异。当杠杆率大于0时，表示两个事件之间存在正向关联。当杠杆率等于0时，表示两个事件之间不存在关联。当杠杆率小于0时，表示两个事件之间存在负向关联。

    • conviction（确信度）是关联规则分析中的另一个度量，用于衡量规则的可靠性。它表示如果前提事件发生，则导致结论事件不发生的概率与假设前提事件和结论事件是独立事件的情况下导致结论事件不发生的概率之比。当确信度大于1时，表示前提事件对于导致结论事件的发生有积极影响。当确信度等于1时，表示前提事件对于导致结论事件的发生没有影响。当确信度小于1时，表示前提事件对于导致结论事件的发生具有负面影响。

    • zhangs_metric（张氏度量）是关联规则分析中的另一个度量，用于衡量规则的置信度和支持度之间的关系。它的计算方式是将置信度和支持度相乘后开方。张氏度量的取值范围在0到1之间，值越接近1表示规则越强。

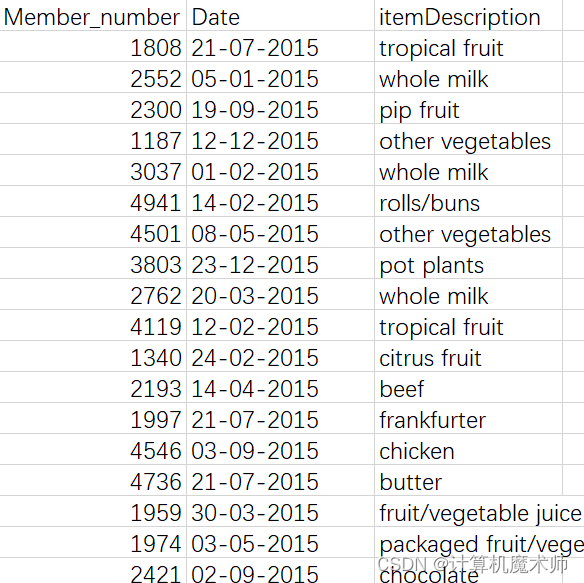
    经典案例：
    我们将使用一个经典的数据集，称为"Groceries"，该数据集包含一段时间内超市顾客购买的物品清单。我们将使用Python中的mlxtend库来实现Apriori算法。

    数据集获取链接: https://www.kaggle.com/datasets/heeraldedhia/groceries-dataset （Dataset of 38765 rows for Market Basket Analysis）

    最流行的是mlxtend包。mlxtend是一个Python库（Machine Learning Extensions)，旨在为机器学习领域提供额外的功能和扩展，以丰富机器学习工具箱，其中包括Apriori算法。

    下面是一个使用mlxtend库的模板代码：

    from mlxtend.preprocessing import TransactionEncoder
    from mlxtend.frequent_patterns import apriori, association_rules
    import pandas as pd
    
    # 加载数据集(简单)
    dataset = [["牛奶", "洋葱", "鸡蛋"],
               ["洋葱", "肉", "鸡蛋", "香蕉"],
               ["牛奶", "苹果", "鸡蛋"],
               ["牛奶", "洋葱", "肉", "鸡蛋"],
               ["洋葱","苹果", "鸡蛋"],
               ["鸡蛋", "苹果"],
               ["洋葱", "牛奶", "苹果", "鸡蛋"]]
    
    # 处理数据
    # 读取数据集
    data = pd.read_csv('grocery_store.csv', header=None)
    
    # 数据预处理
    transactions = []
    for i in range(len(data)):
        transactions.append([str(data.values[i, j]) for j in range(len(data.columns))])
    # 根据同一名用户同一时间作为一行数据
    
       
    # 转换数据集为布尔矩阵
    te = TransactionEncoder()
    te_ary = te.fit(dataset).transform(dataset)
    df = pd.DataFrame(te_ary, columns=te.columns_)
    
    # 使用Apriori算法找出频繁项集
    frequent_itemsets = apriori(df, min_support=0.2, use_colnames=True)
    
     # 计算关联规则的置信度和支持度
      rules = association_rules(frequent_itemsets, metric="confidence", min_threshold=0.7)
    print(rules)
    

不使用库的模板代码：

#-*- coding: utf-8 -*-
from __future__ import print_function
import pandas as pd

#自定义连接函数，用于实现L_{k-1}到C_k的连接
def connect_string(x, ms):
  x = list(map(lambda i:sorted(i.split(ms)), x))
  l = len(x[0])
  r = []
  for i in range(len(x)):
    for j in range(i,len(x)):
      if x[i][:l-1] == x[j][:l-1] and x[i][l-1] != x[j][l-1]:
        r.append(x[i][:l-1]+sorted([x[j][l-1],x[i][l-1]]))
  return r

#寻找关联规则的函数
def find_rule(d, support, confidence, ms = u'--'):
  result = pd.DataFrame(index=['support', 'confidence']) #定义输出结果
  
  support_series = 1.0*d.sum()/len(d) #支持度序列
  column = list(support_series[support_series > support].index) #初步根据支持度筛选
  k = 0
  
  while len(column) > 1:
    k = k+1
    print(u'\n正在进行第%s次搜索...' %k)
    column = connect_string(column, ms)
    print(u'数目：%s...' %len(column))
    sf = lambda i: d[i].prod(axis=1, numeric_only = True) #新一批支持度的计算函数
    
    #创建连接数据，这一步耗时、耗内存最严重。当数据集较大时，可以考虑并行运算优化。
    d_2 = pd.DataFrame(list(map(sf,column)), index = [ms.join(i) for i in column]).T
    
    support_series_2 = 1.0*d_2[[ms.join(i) for i in column]].sum()/len(d) #计算连接后的支持度
    column = list(support_series_2[support_series_2 > support].index) #新一轮支持度筛选
    support_series = support_series.append(support_series_2)
    column2 = []
    
    for i in column: #遍历可能的推理，如{A,B,C}究竟是A+B-->C还是B+C-->A还是C+A-->B？
      i = i.split(ms)
      for j in range(len(i)):
        column2.append(i[:j]+i[j+1:]+i[j:j+1])
    
    cofidence_series = pd.Series(index=[ms.join(i) for i in column2]) #定义置信度序列
 
    for i in column2: #计算置信度序列
      cofidence_series[ms.join(i)] = support_series[ms.join(sorted(i))]/support_series[ms.join(i[:len(i)-1])]
    
    for i in cofidence_series[cofidence_series > confidence].index: #置信度筛选
      result[i] = 0.0
      result[i]['confidence'] = cofidence_series[i]
      result[i]['support'] = support_series[ms.join(sorted(i.split(ms)))]
  
  result = result.T.sort_values(['confidence','support'], ascending = False) #结果整理，输出
  print(u'\n结果为：')
  print(result)
  
  return result

——————————————————————————————————————————————————————————————————————————————————————————
#-*- coding: utf-8 -*-
#使用Apriori算法挖掘菜品订单关联规则
from __future__ import print_function
import pandas as pd
from apriori import * #导入自行编写的apriori函数

inputfile = '../data/menu_orders.xls'
outputfile = '../tmp/apriori_rules.xls' #结果文件
#data = pd.read_excel(inputfile, header = None)
# 加载数据集(简单)
data = [["牛奶", "洋葱", "鸡蛋"],
           ["洋葱", "肉", "鸡蛋", "香蕉"],
           ["牛奶", "苹果", "鸡蛋"],
           ["牛奶", "洋葱", "肉", "鸡蛋"],
           ["洋葱","苹果", "鸡蛋"],
           ["鸡蛋", "苹果"],
           ["洋葱", "牛奶", "苹果", "鸡蛋"]]

print(u'\n转换原始数据至0-1矩阵...')
ct = lambda x : pd.Series(1, index = x[pd.notnull(x)]) #转换0-1矩阵的过渡函数
b = map(ct, data.as_matrix()) #用map方式执行
data = pd.DataFrame(list(b)).fillna(0) #实现矩阵转换，空值用0填充
print(u'\n转换完毕。')
del b #删除中间变量b，节省内存

support = 0.2 #最小支持度
confidence = 0.5 #最小置信度
ms = '---' #连接符，默认'--'，用来区分不同元素，如A--B。需要保证原始表格中不含有该字符

find_rule(data, support, confidence, ms).to_excel(outputfile) #保存结果

相关学习资源：

1. R. Agrawal, R. Srikant. Fast algorithms for mining association rules , 1994
2. mlxtend官方文档：http://rasbt.github.io/mlxtend/
3. Python数据分析与挖掘实战（朱明星 著）- 第12章 关联规则挖掘

						  到这里，如果还有什么疑问
					欢迎私信博主问题哦，博主会尽自己能力为你解答疑惑的！
					 	 如果对你有帮助，你的赞是对博主最大的支持！！