三维模型相机视角投影详细介绍及python程序解析

【版权声明】
本文为博主原创文章，未经博主允许严禁转载，我们会定期进行侵权检索。
更多算法总结请关注我的博客：https://blog.csdn.net/suiyingy，或”乐乐感知学堂“公众号。
本文章来自于专栏《Python三维模型处理基础》的系列文章，专栏地址为：https://blog.csdn.net/suiyingy/category_12462636.html。    

        三维模型在相机视角中投影是指模拟相机观察到的模型图像，其成像效果与相机位置姿态（外参）和相机参数（内参）密切相关。三维点云或模型向固定平面进行投影的原理及其详细python程序请参考博文《python三维点云投影（一）》、《python三维点云投影（二）》，地址分别为“https://blog.csdn.net/suiyingy/article/details/124111743”、“https://blog.csdn.net/suiyingy/article/details/124136567”。这种平面投影是直接进行投影，通常不存在畸变，属于正交投影。本节所介绍的视角投影则属于一种透视变换，更加接近真实成像结果。

        正交投影和透视投影是计算机图形学中常用的两种投影方式。正交投影，也称为平行投影，是指从一个方向上垂直地投射到平面上，类似于我们看物体时所使用的方法。在正交投影中，物体的所有线段都是平行的，没有近大远小的效果，因此适合于制作平面化的图像，比如建筑图纸、工程制图等。透视投影则是一种更加真实和逼真的投影方式，它模拟了人眼在看远近不同的物体时所产生的远近感。在透视投影中，与观察者距离较远的物体看起来比较小，而距离较近的物体则看起来比较大。透视投影通常应用于视觉效果比较重要的情景，比如电影、游戏、虚拟现实等。需要注意的是，在计算机图形学中，正交投影和透视投影都是用投影矩阵来实现的。而具体使用哪种投影方式取决于应用场景和需求。

        在计算机图形学领域，三维模型的投影和旋转是非常重要的基础操作。通过投影，我们可以将三维模型映射到二维平面上，从而方便进行可视化和分析。而旋转则可以改变模型的角度和姿态，使其在不同的视角下展示。下文也会将结合详细的python程序来对比两种方法的投影或成像结果。文中所涉及的详细Python示例程序下载地址为“https://download.csdn.net/download/suiyingy/88471678”，或者在“乐乐感知学堂”內回复“3d处理基础”即可。

1 python环境准备

        首先，我们需要安装一些必要的python库。在这篇文章中，我们将使用以下库进行三维模型的投影和旋转：

        （1）cv2：用于图像处理和显示

        （2）trimesh：用于加载和处理三维模型

        （3）numpy：用于进行数值计算和矩阵操作

        （4）open3d：用于可视化和操作点云数据

        （5）pyrender：用于渲染三维模型

        其中，pyrender是本节示例程序中的核心，后续博文还将介绍基于pyopengl等python库进行渲染投影。你可以通过pip命令来安装这些库：

pip install opencv-python trimesh numpy open3d pyrender

2 示例模型加载与可视化

        本节示例模型为一个近似三棱柱，近似为一系列直立的三角形从左向右（x方向）堆叠而成，其侧面近似为三角形，底面为矩形。示例模型动画如下图所示，默认不加载图像贴图。

图1 示例模型动画

        MeshLab中示例模型显示结果如下图所示，默认会显示贴图效果，即OBJ文件中的RGB信息（与点云顶点坐标位于同一行，并且已经归一化），后续博文会详细介绍python三维模型的贴图方法。这里在软件中显示出了坐标轴，x轴方向朝右，y轴方向朝上，z轴方向朝外，三个坐标轴方向满足右手定则。可以看到，当前为三维模型的俯视图。大多数软件和程序可视化三维模型时都会默认切换到俯视图视角。这相当于在模型正上方放置一个相机观察到的图像，或者相当于我们从顶部观察图像。相机朝向默认为z轴负方向。

图2 MeshLab可视化效果（含坐标轴与纹理）

        我们使用trimesh库加载示例模型。假设我们的模型文件为'model.obj'，你可以将其替换成你自己的模型文件路径。

mesh = trimesh.load('model.obj', force='mesh')
mesh.show()

3 相机设置

        投影是将三维模型映射到二维平面上的过程，我们将采用透视投影的方式进行投影。在进行投影之前，我们需要设置相机的参数，包括焦距、图像宽度和高度等。这些参数会影响最终投影结果的大小和比例。在示例中，我们假设相机的焦距为800和600，图像的宽度和高度也为800和600。

w, h = 800, 600  # 图像的宽度和高度
fx, fy = 800, 600  # 相机焦距

        假设模型在宽度和高度方向上的实际尺寸为W和H，D表示相机距模型的距离。焦距和像距之间有如下近似关系。假设w=fx, 那么D=W；假设h=fy, 那么D=H。也就是说相机放置距离与视野范围相等（且平移到中心位置）时，即可看全整个视野。

w : W = fx : D
h : H = fy : D

        上述关系如下图所示。

图3 成像示意图

        在理想情况下，上述设置可看到整个视野。但是模型自身形状也会对光线形成阻挡。以下图为例，在没有阻挡的情况下，相机可直接看到模型底部AB。但由于模型顶部CD对光线形成了阻挡，这导致实际模型并不能被观察完整。

图4 视线阻挡

        为了使视野可看到更多内容，即增大H和W，我们需要增大距离D或者减小焦距f。这说明距离越远或者焦距越小，则视野越大。下文示例程序中设置了比例因子ratio，可使得视野按照长边距离进行等比例放大。Ratio为0.7和1.0的模型俯视投影图分别如下图所示。显然，Ratio为1.0时投影成像发生了阻挡。

图5 ratio分别为0.7和1.0时的效果图

        相机姿态位置采用维度为3x4的矩阵来进行表示，即旋转和平移矩阵（RT），如下所示。矩阵前3列（旋转矩阵R）表示相机姿态，用于控制成像所在平面，最后一列（平移矩阵T）则表示相机放置的位置坐标（x, y, z）。Pyrender会在最后一行补充[0, 0, 0, 1]使矩阵转换为方阵，维度为4x4，进而可通过矩阵变换实现平移功能（原始待变换坐标x、y、z需要表示为x、y、z、1）。

RT =[R T]=[X Y Z camera_position]
[[r11, r12, r13, x],
[r21, r22, r23, y],
[r31, r32, r33, z]]

4 俯视图

        Pyrender相机默认位置在模型中央上方，并且相机默认朝向为z轴负方向，因而可得到俯视图。因此，旋转矩阵为单位矩阵，即不需要对相机姿态进行旋转操作。我们可以通过平移矩阵控制相机位置，相机放置在模型xy平面中心，并且位于模型顶端。x方向的中心位置为d[0]*ratio/2，y方向中心位置为0，z方向位置由上述内参计算得到。程序中我们将相机位姿矩阵RT设置如下：

camera_pose = np.array([
        [1.0, 0.0, 0.0, d[0]*ratio/2],#相机x方向的位置
        [0.0, 1.0, 0.0, 0.0],  # 设置相机位置为 (d[0]*0.7/2, 0, max(d[0], d[1]))
        [0.0, 0.0, 1.0, max(d[0], d[1])],
        [0.0, 0.0, 0.0, 1.0]
])

        构建场景：接下来，我们使用pyrender库构建一个场景。场景中包含了三维模型和相机。

scene = Scene(ambient_light=np.array([1.0, 1.0, 1.0, 1.0]), bg_color=[1,0,0,1])
# 添加模型到场景中
scene_mesh = Mesh.from_trimesh(mesh)
scene.add(scene_mesh)
# 添加相机到场景中
camera_pose = np.array([
    [1.0, 0.0, 0.0, d[0]*0.7/2],  # 模型x方向中心位置
    [0.0, 1.0, 0.0, 0.0],
    [0.0, 0.0, 1.0, max(d[0], d[1])],
    [0.0, 0.0, 0.0, 1.0]
])
camera_intrinsics = IntrinsicsCamera(fx=fx, fy=fy, cx=w/2, cy=h/2)
scene.add(camera_intrinsics, pose=camera_pose)

        渲染图像：最后，我们使用OffscreenRenderer类对场景进行渲染，并得到投影后的图像。

renderer = OffscreenRenderer(w, h)
color_image, _ = renderer.render(scene)

        示例模型俯视图成像结果如下图所示。详细Python示例程序下载地址为“https://download.csdn.net/download/suiyingy/88471678”，或者在”乐乐感知学堂“內回复”3d处理基础“即可。

图6 俯视图

5 左视图

        假设三维模型的原始坐标系为x、y、z。三维模型坐标系x轴方向朝右，y轴方向朝里，z轴方向朝上，三个坐标轴方向满足右手定则。左视图成像时，相机从左侧看向右侧，因此其z轴方向朝左，与相机朝向相反，即z=-x（[-1, 0, 0]）。假设将高度方向作为y轴，那么y=z（[0, 0, 1]）。根据右手定则，相机x轴方向朝里，即x=-y（[0, -1, 0]）。因此，相机姿态矩阵R计算结果为

R = [[0, 0, -1],
[-1, 0, 0],
[0, 1, 0]]。

        R的列向量分别对应x轴、y轴和z轴。原始坐标系和变换后坐标系示意图如下。

图7 左视图坐标系变换

        左视图示例程序中将相机放置在x轴上，平移T矩阵设置为 [-max(d[1], d[2]), 0.0, 0.0]。矩阵的坐标位置可通过上述介绍的相机内参变换关系计算得到。因此，相机位姿矩阵RT设置如下：

camera_pose = np.array([
    [0.0, 0.0, -1.0, -max(d[1], d[2])],  # 设置相机位置
    [-1.0, 0.0, 0.0, 0.0],
    [0.0, 1.0, 0.0, 0.0],
    [0.0, 0.0, 0.0, 1.0]
    ])

        示例模型左视图成像结果如下图所示。详细Python示例程序下载地址为“https://download.csdn.net/download/suiyingy/88471678”，或者在“乐乐感知学堂”內回复“3d处理基础”即可。

图8 示例模型左视图

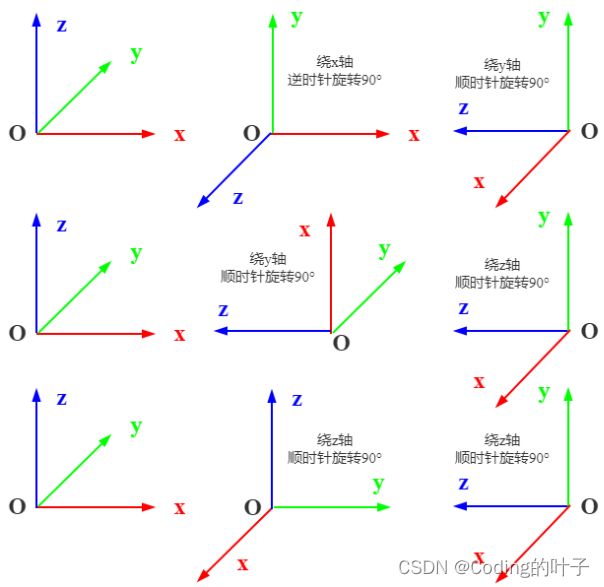
6 旋转投影

        原始坐标方向为x轴朝右、y轴朝里、z轴朝上，左视图中x轴朝外、y轴朝上、z轴朝右。相机放置在z轴正方向，并看向z轴负方向。根据前文所述，相机位姿旋转矩阵R的实际意义表示了相机的朝向，可通过旋转操作得到。

        下图中展示了3种可将原始坐标系转换为左视图坐标系的方案，分别为：

        （1）绕x轴逆时针旋转90°，再绕y轴顺时针旋转90°。

        （2）绕y轴顺时针旋转90°，再绕z轴顺时针旋转90°

        （3）绕z轴顺时针旋转90°，再绕x轴逆时针旋转90°

图8 三种旋转过程示意图

        根据旋转角度可计算得到旋转矩阵，详细计算原理和过程请参考博文《点云旋转平移（一）—基础知识介绍》和《点云旋转平移（三）—python open3d点云旋转》，地址分别为“https://blog.csdn.net/suiyingy/article/details/124374486”和“https://blog.csdn.net/suiyingy/article/details/124403277”。Open3d中提供了相应函数，关键程序如下所示。详细Python示例程序下载地址为“https://download.csdn.net/download/suiyingy/88471678”，或者在“乐乐感知学堂”內回复“3d处理基础”即可。

pcd = o3d.geometry.PointCloud()
# 左视图
R = pcd.get_rotation_matrix_from_xyz((np.pi/2, -np.pi/2, 0))  # 绕x轴逆时针旋转90°，再绕y轴顺时针旋转90
R = pcd.get_rotation_matrix_from_xyz((0, -np.pi/2, -np.pi/2)) # 绕y轴顺时针旋转90°，再绕z轴顺时针旋转90°
R = pcd.get_rotation_matrix_from_zyx((-np.pi/2, 0, np.pi/2))  # 绕z轴顺时针旋转90°，再绕x轴顺时针旋转90°
print('R: ', R)

        Open3d计算结果与上一节完全一致，验证了我们的描述过程。这里需要注意旋转方向。一般情况下，逆时针旋转角度为正，顺时针旋转角度为负。方向判断可通过右手定则。拇指方向沿着旋转轴正方向，当旋转方向与四指弯曲方向一致时，其为逆时针方向；当旋转方向与四指弯曲方向相反时，其为顺时针方向。

7 方向向量投影

        根据上文描述，旋转矩阵关键设置来源于相机朝向，即变换后的z轴方向。假设新的z轴用向量n1来表示，在左视图中n1可表示为[-1, 0, 0]。原始坐标系的z轴用向量n0来表示，取值为[0, 0, 1]。我们的目标是将向量n0旋转到n1，那么旋转轴向量r_axis通过向量叉乘即可得到。在open3d中，旋转轴向量的模长为旋转角度，即n0和n1之间的夹角，并且根据旋转轴向量可求得旋转矩阵，过程如下所示。

# 默认z轴方向
n0 = np.array([0, 0, 1])
# 计算旋转角度
the = np.arccos(np.dot(n0, n1) /  np.linalg.norm(n0) / np.linalg.norm(n1))
# 根据向量叉乘计算旋转轴
r_axis = np.cross(n0, n1)
# open3d中旋转向量的模长表示旋转角度
r_axis = r_axis / np.linalg.norm(r_axis) * the

# 计算旋转矩阵
pcd = o3d.geometry.PointCloud()
R = pcd.get_rotation_matrix_from_axis_angle(r_axis.T)
pcd.rotate(R)

        将z轴调整好之后，我们可以通过控制绕z轴的旋转来控制成像平面的角度。以左视图为例，我们需要绕z轴顺时针旋转90°，并得到相应的旋转矩阵。上述两个旋转矩阵相乘即可得到最终RT矩阵。关键程序如下所示，详细Python示例程序下载地址为“https://download.csdn.net/download/suiyingy/88471678”，或者在“乐乐感知学堂”內回复“3d处理基础”即可。

# 绕z轴再次旋转
rz = pcd.get_rotation_matrix_from_xyz((0, 0, theta))
R = R.dot(rz)
print('R2: ', R)

8 参考文献

        （1）OpenCV官方文档：https://docs.opencv.org/

        （2）trimesh官方文档：https://trimsh.org/

        （3）open3d官方文档：http://www.open3d.org/docs/

        （4）pyrender官方文档：https://pyrender.readthedocs.io/

        本文介绍了如何使用Python进行三维模型的投影和旋转。通过使用开源库，我们可以方便地对模型进行可视化和分析。投影可以将三维模型映射到二维平面上，便于观察和处理。旋转可以改变模型的角度和姿态，从不同的视角来观察模型。希望本文能够对你理解三维图形学领域的投影和旋转有所帮助。

【版权声明】
本文为博主原创文章，未经博主允许严禁转载，我们会定期进行侵权检索。
更多算法总结请关注我的博客：https://blog.csdn.net/suiyingy，或”乐乐感知学堂“公众号。
本文章来自于专栏《Python三维模型处理基础》的系列文章，专栏地址为：https://blog.csdn.net/suiyingy/category_12462636.html。