模拟退火算法（SA）求解旅行商问题（TSP）python

目录

一、模拟退火算法求解TSP（city14）的python代码

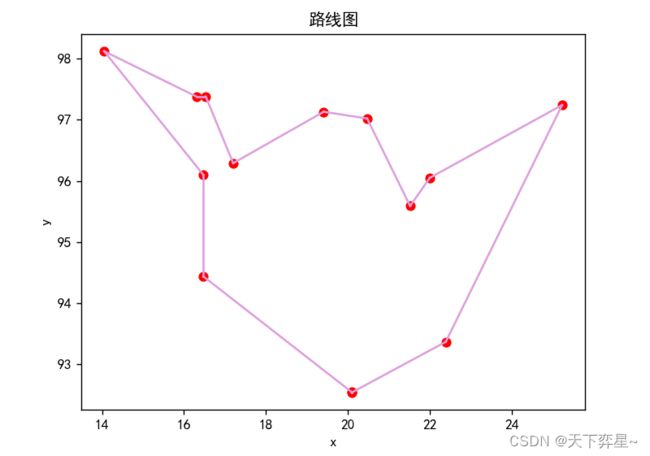
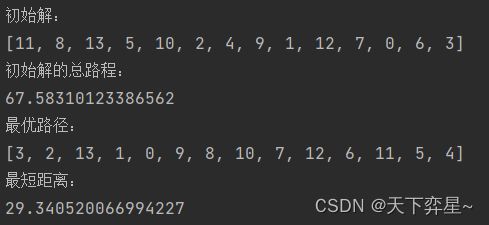
二、city14的运行结果

三、 模拟退火算法求解TSP（city30）的python代码

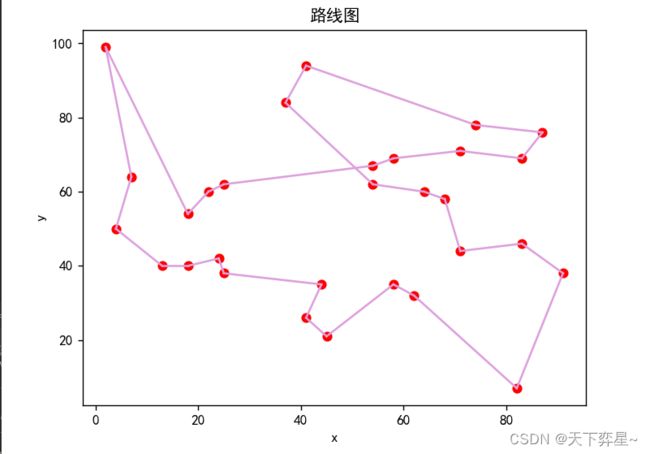
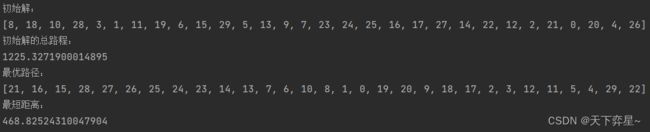
四、city30的运行结果

---

一、模拟退火算法求解TSP（city14）的python代码

import random
import numpy as np
import math
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False


'''计算路径总路程的函数'''
def fitness(n,X,Y,X0):
    '''
    :param n: 城市数量
    :param X: n个城市的横坐标
    :param Y: n个城市的纵坐标
    :param X0: 一个解向量
    :return: 总路程
    '''
    s=0
    for i in range(n):
        if i!=n-1:
            s=s+np.sqrt((X[X0[i]]-X[X0[i+1]])**2+(Y[X0[i]]-Y[X0[i+1]])**2)
        else:
            s=s+np.sqrt((X[X0[i]]-X[X0[0]])**2+(Y[X0[i]]-Y[X0[0]])**2)
    return s


'''定义领域搜索运算操作——交换操作'''
def exchange(X0,q):
    '''
    :param X0: 一个解向量
    :param q: 指定的需要交换的数的两个位置的列表，列表长度为2
    :return: 一个领域解
    '''
    X1=X0.copy()
    temp=X1[q[0]]
    X1[q[0]]=X1[q[1]]
    X1[q[1]]=temp
    return X1


'''定义随机产生初始解的函数'''
def initialX0(n):
    '''
    :param n: 城市数量
    :return: 一个初始解
    '''
    X0=random.sample(range(n),n)
    return X0


'''模拟退火算法——TSP'''
def SA_TSP(n,X,Y,n_TK,r,T_f):
    '''
    :param n: 城市数量
    :param X: n个城市的横坐标
    :param Y: n个城市的纵坐标
    :param n_TK: 内循环的迭代次数
    :param T_down: 降温变化
    :param T_f: 终止温度
    :return: 最优路径和最短距离
    '''

    '''产生一个初始解'''
    X0=initialX0(n)
    print("初始解：\n{}".format(X0))
    print("初始解的总路程：\n{}".format(fitness(n,X,Y,X0)))

    '''初始温度'''
    T0=1000

    '''存储历史最优路径'''
    X_min=[]
    X_min.append(X0)

    '''存储历史最优距离'''
    s_min=[]
    s_min.append(fitness(n,X,Y,X0))

    k=0

    while T0>T_f:
        for i in range(n_TK):
            #随机产生两个位置
            q=random.sample(range(n),2)
            #领域运算得到一个随机领域解
            X1=exchange(X0,q)
            #计算初始解和随机领域解的目标函数值
            s1=fitness(n,X,Y,X0)
            s2=fitness(n,X,Y,X1)

            #更新历史最优解
            if s2R:
                    X0=X1

            k=k+1

        '''降温'''
        T0=T0*r

    '''绘制优化过程'''
    plt.plot(range(k+1),s_min)
    plt.grid()
    plt.title("模拟退火算法——TSP的优化过程")
    plt.xlabel("迭代次数")
    plt.ylabel("总路程")
    plt.show()

    '''绘制路线图'''
    #最优路径
    W=X_min[-1]
    for i in range(n):
        if i!=n-1:
            plt.plot([X[W[i]],X[W[i+1]]],[Y[W[i]],Y[W[i+1]]],c='plum')
        else:
            plt.plot([X[W[i]],X[W[0]]],[Y[W[i]],Y[W[0]]],c='plum')
    plt.scatter(X,Y,c='red')
    plt.title("路线图")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.show()

    return X_min[-1],s_min[-1]



'''主函数'''
if __name__=="__main__":

    '''城市的数量'''
    n=14

    '''定义14个城市的坐标'''
    city_x=[16.47,16.47,20.09,22.39,25.23,22.00,20.47,17.20,16.30,14.05,16.53,21.52,19.41,20.09]
    city_y=[96.10,94.44,92.54,93.37,97.24,96.05,97.02,96.29,97.38,98.12,97.38,95.59,97.13,92.55]

    '''内循环的迭代次数'''
    n_Tk=200

    '''降温变化'''
    r=0.9

    '''终止温度'''
    T_f=0.001

    '''模拟退火算法求解TSP'''
    Xmin,smin=SA_TSP(n,city_x,city_y,n_Tk,r,T_f)

    print("最优路径：\n{}".format(Xmin))
    print("最短距离：\n{}".format(smin))

二、city14的运行结果

 

三、 模拟退火算法求解TSP（city30）的python代码

import random
import numpy as np
import math
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False


'''计算路径总路程的函数'''
def fitness(n,X,Y,X0):
    '''
    :param n: 城市数量
    :param X: n个城市的横坐标
    :param Y: n个城市的纵坐标
    :param X0: 一个解向量
    :return: 总路程
    '''
    s=0
    for i in range(n):
        if i!=n-1:
            s=s+np.sqrt((X[X0[i]]-X[X0[i+1]])**2+(Y[X0[i]]-Y[X0[i+1]])**2)
        else:
            s=s+np.sqrt((X[X0[i]]-X[X0[0]])**2+(Y[X0[i]]-Y[X0[0]])**2)
    return s


'''定义领域搜索运算操作——交换操作'''
def exchange(X0,q):
    '''
    :param X0: 一个解向量
    :param q: 指定的需要交换的数的两个位置的列表，列表长度为2
    :return: 一个领域解
    '''
    X1=X0.copy()
    temp=X1[q[0]]
    X1[q[0]]=X1[q[1]]
    X1[q[1]]=temp
    return X1


'''定义随机产生初始解的函数'''
def initialX0(n):
    '''
    :param n: 城市数量
    :return: 一个初始解
    '''
    X0=random.sample(range(n),n)
    return X0


'''模拟退火算法——TSP'''
def SA_TSP(n,X,Y,n_TK,r,T_f):
    '''
    :param n: 城市数量
    :param X: n个城市的横坐标
    :param Y: n个城市的纵坐标
    :param n_TK: 内循环的迭代次数
    :param T_down: 降温变化
    :param T_f: 终止温度
    :return: 最优路径和最短距离
    '''

    '''产生一个初始解'''
    X0=initialX0(n)
    print("初始解：\n{}".format(X0))
    print("初始解的总路程：\n{}".format(fitness(n,X,Y,X0)))

    '''初始温度'''
    T0=2000

    '''存储历史最优路径'''
    X_min=[]
    X_min.append(X0)

    '''存储历史最优距离'''
    s_min=[]
    s_min.append(fitness(n,X,Y,X0))

    k=0

    while T0>T_f:
        for i in range(n_TK):
            #随机产生两个位置
            q=random.sample(range(n),2)
            #领域运算得到一个随机领域解
            X1=exchange(X0,q)
            #计算初始解和随机领域解的目标函数值
            s1=fitness(n,X,Y,X0)
            s2=fitness(n,X,Y,X1)

            #更新历史最优解
            if s2R:
                    X0=X1

            k=k+1

        '''降温'''
        T0=T0*r

    '''绘制优化过程'''
    plt.plot(range(k+1),s_min)
    plt.grid()
    plt.title("模拟退火算法——TSP的优化过程")
    plt.xlabel("迭代次数")
    plt.ylabel("总路程")
    plt.show()

    '''绘制路线图'''
    #最优路径
    W=X_min[-1]
    for i in range(n):
        if i!=n-1:
            plt.plot([X[W[i]],X[W[i+1]]],[Y[W[i]],Y[W[i+1]]],c='plum')
        else:
            plt.plot([X[W[i]],X[W[0]]],[Y[W[i]],Y[W[0]]],c='plum')
    plt.scatter(X,Y,c='red')
    plt.title("路线图")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.show()

    return X_min[-1],s_min[-1]



'''主函数'''
if __name__=="__main__":

    '''城市的数量'''
    n=30

    '''定义30个城市的坐标'''
    city_x=[41, 37, 54, 25, 7, 2, 68, 71, 54, 83, 64, 18, 22, 83, 91, 25, 24, 58, 71, 74, 87,
            18, 13, 82, 62, 58, 45,41,44, 4]
    city_y=[94, 84, 67, 62, 64, 99, 58, 44, 62, 69, 60, 54, 60, 46, 38, 38, 42, 69, 71, 78, 76,
            40, 40, 7, 32, 35, 21,26,35, 50]

    '''内循环的迭代次数'''
    n_Tk=300

    '''降温变化'''
    r=0.9

    '''终止温度'''
    T_f=0.001

    '''模拟退火算法求解TSP'''
    Xmin,smin=SA_TSP(n,city_x,city_y,n_Tk,r,T_f)

    print("最优路径：\n{}".format(Xmin))
    print("最短距离：\n{}".format(smin))

四、city30的运行结果