机器学习之数据预备、清洗与特征工程
-
- 一、概念:
- 二、为什么要进行预处理:
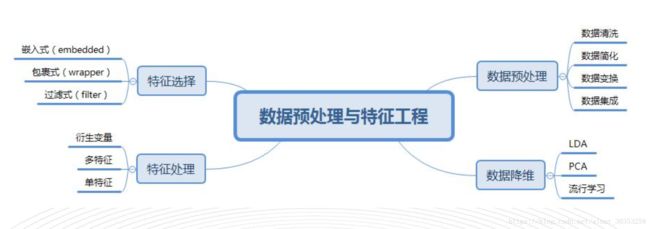
- 1-1 数据预处理简介
- 为什么要进行预处理:
- 数据预处理的功能:
- ① 数据集成(Data Integration)详解:
- ② 数据变换( Bata Trartsformstian ) 详解:
- ③ 数据清洗(Data Cleaning )详解:
- ④ 数据简化(Data simplify)详解:
- a、维归约(dimensionlity):
- b、数量归约(numerosity reduction):
- c、数据压缩(data compression):
- 1-2 数据的降维处理
- 一、什么是数据降维:
- 二、为什么要数据降维:
- 三、数据降维的常见方法:
- ( 1) LDA(线性判别式分析)法:
- (2) PCA(主成分分析)法:
- ( 3) PCA与LDA方法的区别:
- 1-1 数据预处理简介
一、概念:
数据预处理:将未加工数据转换成适合分析的形式,包括多数据源的数据融合、
数据清洗、维规约等等。
二、为什么要进行预处理:
1-1 数据预处理简介
原始数据普遍存在问题,必须加以处理才能用于分析,一方面要提高数据质量,另一方
面为了更好的使数据适应特定的数据挖掘技术及工具。
举例①:
将连续值(长度)转化为离散的分类值属性(短,中,长),以便应用特定算法模型。
举例②:
减少数据集属性数目,以便后续使用算法模型更加有效。
为什么要进行预处理:
| 名称 | 描述 | 原因 |
|---|---|---|
| 杂乱性 | 数据缺乏统一标准和定义,数据结构有较大的差异 | 原始数据一般是从各个实际应用系统中获取的(多种数据库、多种文件系统),而这些系统的格式并不相同。 |
| 重复性 | 指对于同一个客观事物在数据库中存在其两个或两个以上完全相同的描述 | 由于业务的交叉和重叠,几乎所有系统中都存在数据的重复和信息的冗余现象。 |
| 不完整性 | 大量的模糊信息,某些数据设置的随机性,数据的缺失等 | 由于实际系统设计时存在的缺陷以及一些使用过程中人为因素所造成 |
数据预处理的功能:
① 数据集成(Data Integration)详解:
把不同来源、 格式、 特点性质的数据在逻辑上或物理上有机地集中, 从而为企业提供
全面的数据共享。
统一原始数据的矛盾之处(如命名、 结构、 单位、 含义):
如字段的同名异义、 异名同义、 单位不统一、 字长不一致等,并非简单的复制过程。
② 数据变换( Bata Trartsformstian ) 详解:
[Source]© Onedot Ltd.
通常用多维数据立方(Data Cube)组织数据, 采用数据仓库中的切换、 旋转和投影技术,
把数据空间按照不同的层次、 粒度和维度进行抽象和聚集(即数据泛化), 从而生成在
不同抽象级别上的数据集。
数据变换一般方法:
| 平滑 | 去掉数据中的噪音。 | 常用包括分箱、 聚类和回归 |
|---|---|---|
| 聚集 | 对数据进行汇总和聚集。 这一步用来为多粒度数据分析构造数据方。 | 聚集日销售数据, 计算月和年销售额 |
| 数据泛化 | 使用概念分层, 用高层次概念替换低层次“原始”数据 | 分类, 如street, 泛化为较高层的概念,如city , country。数值, 如age, 映射到较高层概念, 如young, middle-age, senior。 |
| 规范化 | 将属性数据按比例缩放, 使之落入一个小的特定区间 | 如将数据比例缩放到[-1.0 ,1.0] 或[0.0 ,1.0]。 |
| 属性构造(特征构造) | 构造新的属性并添加到属性集中,以帮助挖掘过程 | 平方根转换, 平方转换等 |
③ 数据清洗(Data Cleaning )详解:
Sklearn自带的数据, 譬如iris数据集, 波士顿房价数据集, 质量都很高, 没有缺失值, 没有异常点, 也没有噪音。
真实数据中, 我们拿到的数据可能包含了大量的缺失值, 噪音, 也可能因为人工录入错误导致有异常点存在, 所以我们需要通过一些方法,尽量提高数据的质量。
噪声: 被测量的变量的随机误差或者方差(一般指错误的数据)
离群点: 数据集中包含一些数据对象, 他们与数据的一般行为或模型不一致。
(正常值, 但偏离大多数数据)
观测量(Measurement) = 真实数据(True Data) + 噪声 (Noise)
- 缺失值:由于人为或系统原因遗漏的值。
- 异常值:通常称为离群点(Outlier), 属于观测量, 既有可能是真实数据产生的, 也有可能是噪声带来的, 但和大部分观测量之间有明显不同的观测值。
- 去重复:对于同一个客观事物在数据库中存在其两个或两个以上完全相同的物理描述
- 噪音:噪音包括错误值或偏离期望的孤立点值
- ETL方法:即抽取(extract) 、 转换(transform) 、 加载(load)
代码实现:
import numpy as np
from sklearn.preprocessing import Imputer
#使用sklearn.preprocessing.Imputer类来处理
#使用np.nan对缺失值进行编码过的数据集
imp = Imputer(missing_values='NaN', strategy='mean', axis=0)
X=np.array([[1,5], [np.nan,4], [8,7]])
#使用字符串'nan'来代替数据集中的缺失值
Y=[[np.nan,2], [6, np.nan], [7,6]]
A=imp.fit(X)
B=imp.transform(Y)
# 使用数组X去“训练”一个Imputer类
# 然后用该类的对象去处理数组Y中的缺失值
# 缺失值的处理方式是使用X中的均值
#(axis=0表示按列进行) 代替Y中的缺失值
print(B)离群点检测的方法:
| 1 | 2 | 3 |
|---|---|---|
| 基于统计检测 | 假设给定的数据集服从某一随机分布(如正态分布等) , 用不一致性测试识别异常。 | 不适合多维空间, 预先要知道样本空间中数据集的分布特征。 |
| 基于密度检测 | 通过基于局部离群点检测就能在样本空间数据分布不均匀的情况下也可以准确发现 | |
| 基于距离检测 | 如果样本空间D至少有N个样本点与对象O的距离大于d, 那么对象O是以至少N个样本点和距离d为参数的基于距离的离群点。 | 参数的选取非常敏感, 受时间复杂度限制, 不适用于高维稀疏数据集 |
| 基于偏差检测 | 检查一组对象的主要特征来识别离群点,那些些不符合这种特征的数据对象被判定为离群点 | 实际应用少, 在高维数据集中, 很难获得该数据集的主要特征 |
④ 数据简化(Data simplify)详解:
也称为数据“规约”, 指在尽可能保持数据原貌的前提下, 最大限度地精简数据量, 它
小得多, 但是保持原始数据的完整性。 也就是说, 在归约后的数据集上挖掘更有效果,
仍然产生相同( 或几乎形同)的分析结果。 注意: 用于数据归约的时间不应当超过或“抵
消”在归约后的数据挖掘上挖掘节省的时间。
常见方法:
a、维归约(dimensionlity):
也称“降维”, 减少要考虑的变量及属性的个数。 方法包括小波变换和主成分分析, 他们把原始数据变换或投影到较小的空间。 另外属性子集选择也是一种维归约方法, 其中不相关、 弱相关或冗余的属性或维被检测和删除。
b、数量归约(numerosity reduction):
用替代的、 较小的数据表示形式替换原始数据
c、数据压缩(data compression):
使用变换, 以便得到原始数据的归约或“压缩”表示。如果原始数据可以从压缩后的数据重构, 而不损失信息, 则该数据归约称为无损的。 反之, 称之为有损的。 维归约和数量归约也可以视为某种形式的数据压缩
1-2 数据的降维处理
一、什么是数据降维:
( 1) 概念: 将数据从高维特征空间向低纬特征空间映射的过程。
( 2) 目的: 直观地好处是维度降低了, 便于计算和可视化, 其更深层次的意义在于有效信息的提取综合及无用信息的摈弃。
二、为什么要数据降维:
( 1) 真实的训练数据总是存在各种各样的问题:
比如拿到一个汽车的样本, 里面既有以“千米/每小时”度量的最大速度特征, 也有“英里/小时”的最大速度特征, 显然这两个特征有一个多余。
(2) 数据降维原因汇总:
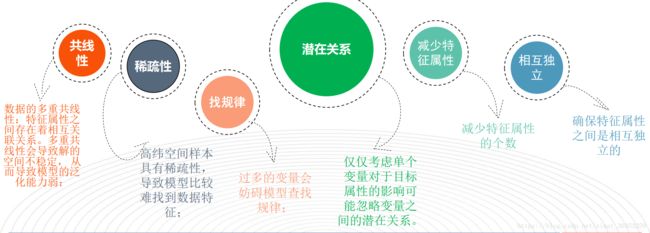
( 3) 数据降维的好处:
有时候也存在特征矩阵过大, 导致计算量比较大,训练时间长的问题。降维可以方便数据可视化+数据分析+数据压缩+数据提取等。
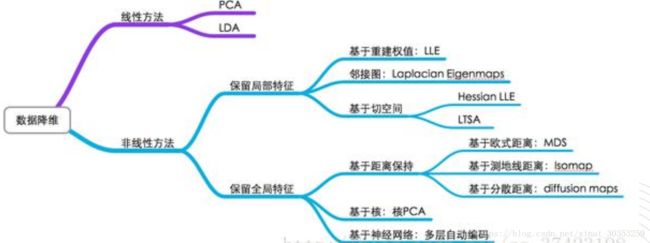
三、数据降维的常见方法:
降维的方法:
LDA 线性判别分析
投影 有监督
方法:投影后类内方差最小,类间方差最大。
( 1) LDA(线性判别式分析)法:
LDA的思想可以用一句话概括,就是“投影后类内方差最小,类间方差最大”。我们要将数
据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的
数据的类别中心之间的距离尽可能的大
投影后类内方差最小,类间方差最大:
每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大
(2) PCA(主成分分析)法:
主成分分析(Principal components analysis,以下简称PCA)是重要的降维方法之一。
PCA顾名思义,就是找出数据里最主要的方面,用数据里最主要的方面来代替原始数据。
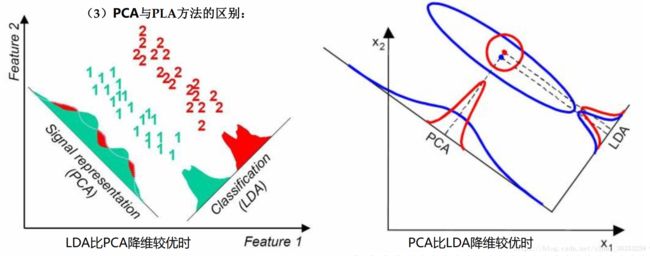
( 3) PCA与LDA方法的区别:
1) 在降维过程中可以使用类别的先验知识经验, 而像PCA这样的无监督学习则无法使用类别先验知识。
2) LDA在样本分类信息依赖均值而不是方差的时候, 比PCA之类的算法较优。
- LDA不适合对非高斯分布样本进行降维, PCA也有这个问题。
- LDA降维最多降到类别数k-1的维数,如果我们降维的维度大于k-1, 则不能使用LDA。 当然目前有一些LDA的进化版算法可以绕过这个问题。
- LDA在样本分类信息依赖方差而不是均值的时候, 降维效果不好。
- LDA可能过度拟合数据
1)两者均可以对数据进行降维。
2)两者在降维时均使用了矩阵特征分解的思想。
3)两者都假设数据符合高斯分布
1)LDA是有监督的降维方法,而PCA是无监督的降维方法
2)LDA降维最多降到类别数k-1的维数,而PCA没有这个限制。
3)LDA除了可以用于降维,还可以用于分类。
4)LDA选择分类性能最好的投影方向,而PCA选择样本点投影具有最大方差的方向。
( 4) 流形学习方法:
流形学习贡献了很多降维算法ISOMAP就是‘流形学习’中的一个经典算法:
Geodesic Distance( 测地距离):
“geodesic”( 测地线) 一词来源于 geodesy( 测地学) , 是一门测量地球大小和形状的学科。 就从 geodesic 的本意来说, 就是地球表面两点之间的最短路径
Geodesic Distance 就是图中两节点的最短路径。
几何空间通常用到的 Euclidean Distance(欧氏距离) , 即两点之间的最短距离, 两者有所
区别。
1.通过kNN(k-Nearest Neighbor)找到点的k个最近邻,将它们连接起来构造一张图。
2.通过计算图中各点之间的最短路径,作为点之间的距离dij放入距离矩阵D
3.将D传给流形学习算法(MDS),得到降维后的结果

小结:
( 1) 不同降维算法对比:

(2)常用降维方法: