【机器学习】决策树(理论与代码)
文章目录
一、理论部分
二、代码实现
1、代码解释。
2、完整代码
3、可视化
一、理论部分
下班到家,打开博客,源码实现下决策树。
理论部分这里不再详细讲。计算可以参考周志华西瓜书。
计算信息熵Ent(D)与信息增益Gain(D)。
原理的话就是选取信息增益最大的为根,以此类推。
观察公式可以看到:
信息增益Gain(D)= 根节点信息熵(X) - 权重*分支节点信息熵和(Y)= X - Y
由于根节点确定后 X不变,要选取最大Gain(D),就是选择最小Y。
因为Y计算过程会取负数,所以选择节点时只需取 乘积和的最大值就行了。
二、代码实现
1、代码解释。
老样子还是fit 函数 。x是特征数据集,y是结果集,多出的x_label是各个特征对应的标签
np.c_[x,y] 拼接x,y。下面看下build_tree 构建树的函数
def fit(self,x,y,x_label):
self.label = x_label # x数据集对应的 特征标签
numpy_data = np.c_[x,y] # 把x,y拼接成一个numpy矩阵,方便后面操作
self.tree = self.build_tree(numpy_data) # 构建树
这部分是构建树,在代码里解释,可以看注释。直接上代码
import numpy as np
class DecisionTree():
def fit(self,x,y,x_label):
self.label = x_label # x数据集对应的 特征标签
numpy_data = np.c_[x,y] # 把x,y拼接成一个numpy矩阵,方便后面操作
self.tree = self.build_tree(numpy_data) # 构建树
def build_tree(self,numpy_data): # numpy_data n行m列的矩阵,最后一列是结果集。返回字典
"""
判断结束:如果最后一列去重后为一个值就结束
最后分类全部是ng或者ok时递归,不能再分 !!!关键点1!!!
这里还有一种情况,就是所有的特征值都一样,但结果不同
我们可以选择取结果多的为return值。(暂不考虑,实现也不难)
"""
finish_columns = np.unique(numpy_data)[:,-1]
if len(finish_columns) == 1:
return finish_columns [0] # 返回ng与ok,表面这个分支已经分到叶子了
rows,columns = numpy_data.shape # numpy行数与列数
root_numpy = np.zeros(columns-1) # 构造全为0的numpy数组,保存信息熵数据
# 遍历每个特征。"触感","色泽","敲声",...
for i in range(columns-1):
sum = 0
# 每个特征有多少种,如“纹理” 这个特征 numpy_data为("清晰","稍糊","模糊")
unique_data = np.unique(numpy_data[:,i])
for j in unique_data:
len_whole = len(numpy_data[(numpy_data[:,i] == j)])
len_ng = len(numpy_data[(numpy_data[:i]==j)&(numpy_data[:,-1]=="ng")])
# ok的长度 = 总长度-ng的长度
len_ok = len_whole-len_ng
if len_ng !=0 and len_ok!=0: # 有一个为0就不用参与计算
x = len_ok/len_whole
# 每个特征{x属于(0,1) (x*np.log2(x)+(1-x)log2(1-x))*个数比例}
# 得到单个sum
# 迭代求和
sum = sum + round(len_whole/rows*(x*np.log2(x)+(1-x)*np.log2(1-x)),3)
root_numpy[i] = sum # 保存各个特征的信息熵
root = root_numpy.argsort()[-1] # -1 选取最大值索引。np.argsort():排序后的索引
"""
构建字典存放树的数据
计算得到 tree_dict为:{"纹理":{}}
"""
tree_dict = {self.label[root]:{}}
# print(tree_dict)
"""
拿到根节点为“纹理”后还要继续分
np.unique(numpy_data[:,root])计算根节点后面有几分支,("清晰"、"稍糊"、"模糊")继续分
"""
for values in np.unique(numpy_data[:,root]):
# 把对应的数据进行区分,切割出符合条件的数据后面继续分
numpy_root = numpy_data[(numpy_data[:,root] == values)]
# print(values,numpy_root)
"""
继续往下走,递归后面数据 !!!关键点2!!!
拿到根节点,分支后得到新的数据,新的数据选节点计算方式一样,
递归直到叶子结束。我们已经对数据进行处理了,后面计算方式是一样的
"""
# 字典新的key 继续存
tree_dict[self.label[root]][values] = self.build_tree(numpy_root)
return tree_dict 构造数据集进行计算。这个举例子有点难,我们直接用西瓜书的数据集进行测试,也方便验证。
这里大家可能会有个疑问。
data1,2,3,4,5,6 为什么顺序跟西瓜书不一样呢,因为在计算信息熵的时候,最大值可能有多个值,所以构建的树可能不同,都正确。西瓜书选取的是第一次最大值就分,而np.argsort()取得索引最后一位是最后一次出现的最大值。为了保持一致,顺序调了下。
if __name__ == "__main__":
data2 = ["青绿", "乌黑", "乌黑", "青绿", "浅白", "青绿", "乌黑", "乌黑",
"乌黑", "青绿", "浅白", "浅白", "青绿", "浅白", "乌黑", "浅白", "青绿"]
data6 = ["蜷缩", "蜷缩", "蜷缩", "蜷缩", "蜷缩", "稍蜷", "稍蜷", "稍蜷",
"稍蜷", "硬挺", "硬挺", "蜷缩", "稍蜷", "稍蜷", "稍蜷", "蜷缩", "蜷缩"]
data3 = ["浊响", "沉闷", "浊响", "沉闷", "浊响", "浊响", "浊响", "浊响",
"沉闷", "清脆", "清脆", "浊响", "浊响", "沉闷", "浊响", "浊响", "沉闷"]
data4 = ["清晰", "清晰", "清晰", "清晰", "清晰", "清晰", "稍糊", "清晰",
"稍糊", "清晰", "模糊", "模糊", "稍糊", "稍糊", "清晰", "模糊", "稍糊"]
data5 = ["凹陷", "凹陷", "凹陷", "凹陷", "凹陷", "稍凹", "稍凹", "稍凹",
"稍凹", "平坦", "平坦", "平坦", "凹陷", "凹陷", "稍凹", "平坦", "稍凹"]
data1 = ["硬滑", "硬滑", "硬滑", "硬滑", "硬滑", "软粘", "软粘", "硬滑",
"硬滑", "软粘", "硬滑", "软粘", "硬滑", "硬滑", "软粘", "硬滑", "硬滑"]
result = ["ok", "ok", "ok", "ok", "ok", "ok", "ok", "ok",
"ng", "ng", "ng", "ng", "ng", "ng", "ng", "ng", "ng"]
x_label = ["触感", "色泽", "敲声", "纹理", "脐部", "根蒂"]
x = np.array([data1, data2, data3, data4, data5, data6]).transpose()
y = np.array(result)
# print("标签:",x_label)
# print(x)
decisionTree = DecisionTree()
decisionTree.fit(x, y, x_label)
print(decisionTree.tree)
"""
# print("标签:",x_label)
# print(x)
标签: ['触感', '色泽', '敲声', '纹理', '脐部', '根蒂']
[['硬滑' '青绿' '浊响' '清晰' '凹陷' '蜷缩']
['硬滑' '乌黑' '沉闷' '清晰' '凹陷' '蜷缩']
['硬滑' '乌黑' '浊响' '清晰' '凹陷' '蜷缩']
['硬滑' '青绿' '沉闷' '清晰' '凹陷' '蜷缩']
['硬滑' '浅白' '浊响' '清晰' '凹陷' '蜷缩']
['软粘' '青绿' '浊响' '清晰' '稍凹' '稍蜷']
['软粘' '乌黑' '浊响' '稍糊' '稍凹' '稍蜷']
['硬滑' '乌黑' '浊响' '清晰' '稍凹' '稍蜷']
['硬滑' '乌黑' '沉闷' '稍糊' '稍凹' '稍蜷']
['软粘' '青绿' '清脆' '清晰' '平坦' '硬挺']
['硬滑' '浅白' '清脆' '模糊' '平坦' '硬挺']
['软粘' '浅白' '浊响' '模糊' '平坦' '蜷缩']
['硬滑' '青绿' '浊响' '稍糊' '凹陷' '稍蜷']
['硬滑' '浅白' '沉闷' '稍糊' '凹陷' '稍蜷']
['软粘' '乌黑' '浊响' '清晰' '稍凹' '稍蜷']
['硬滑' '浅白' '浊响' '模糊' '平坦' '蜷缩']
['硬滑' '青绿' '沉闷' '稍糊' '稍凹' '蜷缩']]
print(decisionTree.tree)
{'纹理': {
'模糊': 'ng',
'清晰': {'根蒂': {'硬挺': 'ng', '稍蜷': {'色泽': {'乌黑': {'触感': {'硬滑': 'ok', '软粘': 'ng'}}, '青绿': 'ok'}}, '蜷缩': 'ok'}},
'稍糊': {'触感': {'硬滑': 'ng', '软粘': 'ok'}}
}
}
"""2、完整代码
import numpy as np
class DecisionTree():
def fit(self, x, y, x_label):
self.label = x_label # x数据集对应的 特征标签
numpy_data = np.c_[x, y] # 把x,y拼接成一个numpy矩阵,方便后面操作
self.tree = self.build_tree(numpy_data) # 构建树
def build_tree(self, numpy_data): # numpy_data n行m列的矩阵,最后一列是结果集。返回字典
finish_columns = np.unique(numpy_data[:, -1])
if len(finish_columns) == 1:
return finish_columns[0] # 返回ng与ok,表面这个分支已经分到叶子了
rows, columns = numpy_data.shape # numpy行数与列数
root_numpy = np.zeros(columns - 1) # 构造全为0的numpy数组,保存信息熵数据
for i in range(columns - 1):
sum = 0
unique_data = np.unique(numpy_data[:, i])
for j in unique_data:
len_whole = len(numpy_data[(numpy_data[:, i] == j)])
len_ng = len(numpy_data[((numpy_data[:,i] == j)
& (numpy_data[:, -1] == "ng"))])
len_ok = len_whole - len_ng
if len_ng != 0 and len_ok != 0: # 有一个为0就不用参与计算
x = len_ok / len_whole
sum = sum + round(len_whole / rows *
(x * np.log2(x) + (1-x) * np.log2(1-x)), 3)
root_numpy[i] = sum # 保存各个特征的信息熵
root = root_numpy.argsort()[-1] # -1 选取最大值索引。np.argsort():排序后的索引
tree_dict = {self.label[root]: {}}
for values in np.unique(numpy_data[:, root]):
numpy_root = numpy_data[(numpy_data[:, root] == values)]
tree_dict[self.label[root]][values] = self.build_tree(numpy_root)
return tree_dict
if __name__ == "__main__":
data2 = ["青绿", "乌黑", "乌黑", "青绿", "浅白", "青绿", "乌黑", "乌黑",
"乌黑", "青绿", "浅白", "浅白", "青绿", "浅白", "乌黑", "浅白", "青绿"]
data6 = ["蜷缩", "蜷缩", "蜷缩", "蜷缩", "蜷缩", "稍蜷", "稍蜷", "稍蜷",
"稍蜷", "硬挺", "硬挺", "蜷缩", "稍蜷", "稍蜷", "稍蜷", "蜷缩", "蜷缩"]
data3 = ["浊响", "沉闷", "浊响", "沉闷", "浊响", "浊响", "浊响", "浊响",
"沉闷", "清脆", "清脆", "浊响", "浊响", "沉闷", "浊响", "浊响", "沉闷"]
data4 = ["清晰", "清晰", "清晰", "清晰", "清晰", "清晰", "稍糊", "清晰",
"稍糊", "清晰", "模糊", "模糊", "稍糊", "稍糊", "清晰", "模糊", "稍糊"]
data5 = ["凹陷", "凹陷", "凹陷", "凹陷", "凹陷", "稍凹", "稍凹", "稍凹",
"稍凹", "平坦", "平坦", "平坦", "凹陷", "凹陷", "稍凹", "平坦", "稍凹"]
data1 = ["硬滑", "硬滑", "硬滑", "硬滑", "硬滑", "软粘", "软粘", "硬滑",
"硬滑", "软粘", "硬滑", "软粘", "硬滑", "硬滑", "软粘", "硬滑", "硬滑"]
result = ["ok", "ok", "ok", "ok", "ok", "ok", "ok", "ok",
"ng", "ng", "ng", "ng", "ng", "ng", "ng", "ng", "ng"]
x_label = ["触感", "色泽", "敲声", "纹理", "脐部", "根蒂"]
x = np.array([data1, data2, data3, data4, data5, data6]).transpose()
y = np.array(result)
decisionTree = DecisionTree()
decisionTree.fit(x, y, x_label)
print(decisionTree.tree)
3、可视化
可视化树这里有点难度,用《机器学习实战》的代码
import numpy as np
import matplotlib.pylab as plt
import matplotlib
# 能够显示中文
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['font.serif'] = ['SimHei']
# 分叉节点,也就是决策节点
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
# 叶子节点
leafNode = dict(boxstyle="round4", fc="0.8")
# 箭头样式
arrow_args = dict(arrowstyle="<-")
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
"""
绘制一个节点
:param nodeTxt: 描述该节点的文本信息
:param centerPt: 文本的坐标
:param parentPt: 点的坐标,这里也是指父节点的坐标
:param nodeType: 节点类型,分为叶子节点和决策节点
:return:
"""
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)
def getNumLeafs(myTree):
"""
获取叶节点的数目
:param myTree:
:return:
"""
# 统计叶子节点的总数
numLeafs = 0
# 得到当前第一个key,也就是根节点
firstStr = list(myTree.keys())[0]
# 得到第一个key对应的内容
secondDict = myTree[firstStr]
# 递归遍历叶子节点
for key in secondDict.keys():
# 如果key对应的是一个字典,就递归调用
if type(secondDict[key]).__name__ == 'dict':
numLeafs += getNumLeafs(secondDict[key])
# 不是的话,说明此时是一个叶子节点
else:
numLeafs += 1
return numLeafs
def getTreeDepth(myTree):
"""
得到数的深度层数
:param myTree:
:return:
"""
# 用来保存最大层数
maxDepth = 0
# 得到根节点
firstStr = list(myTree.keys())[0]
# 得到key对应的内容
secondDic = myTree[firstStr]
# 遍历所有子节点
for key in secondDic.keys():
# 如果该节点是字典,就递归调用
if type(secondDic[key]).__name__ == 'dict':
# 子节点的深度加1
thisDepth = 1 + getTreeDepth(secondDic[key])
# 说明此时是叶子节点
else:
thisDepth = 1
# 替换最大层数
if thisDepth > maxDepth:
maxDepth = thisDepth
return maxDepth
def plotMidText(cntrPt, parentPt, txtString):
"""
计算出父节点和子节点的中间位置,填充信息
:param cntrPt: 子节点坐标
:param parentPt: 父节点坐标
:param txtString: 填充的文本信息
:return:
"""
# 计算x轴的中间位置
xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
# 计算y轴的中间位置
yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
# 进行绘制
createPlot.ax1.text(xMid, yMid, txtString)
def plotTree(myTree, parentPt, nodeTxt):
"""
绘制出树的所有节点,递归绘制
:param myTree: 树
:param parentPt: 父节点的坐标
:param nodeTxt: 节点的文本信息
:return:
"""
# 计算叶子节点数
numLeafs = getNumLeafs(myTree=myTree)
# 计算树的深度
depth = getTreeDepth(myTree=myTree)
# 得到根节点的信息内容
firstStr = list(myTree.keys())[0]
# 计算出当前根节点在所有子节点的中间坐标,也就是当前x轴的偏移量加上计算出来的根节点的中心位置作为x轴(比如说第一次:初始的x偏移量为:-1/2W,计算出来的根节点中心位置为:(1+W)/2W,相加得到:1/2),当前y轴偏移量作为y轴
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
# 绘制该节点与父节点的联系
plotMidText(cntrPt, parentPt, nodeTxt)
# 绘制该节点
plotNode(firstStr, cntrPt, parentPt, decisionNode)
# 得到当前根节点对应的子树
secondDict = myTree[firstStr]
# 计算出新的y轴偏移量,向下移动1/D,也就是下一层的绘制y轴
plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
# 循环遍历所有的key
for key in secondDict.keys():
# 如果当前的key是字典的话,代表还有子树,则递归遍历
if isinstance(secondDict[key], dict):
plotTree(secondDict[key], cntrPt, str(key))
else:
# 计算新的x轴偏移量,也就是下个叶子绘制的x轴坐标向右移动了1/W
plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
# 打开注释可以观察叶子节点的坐标变化
# print((plotTree.xOff, plotTree.yOff), secondDict[key])
# 绘制叶子节点
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
# 绘制叶子节点和父节点的中间连线内容
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
# 返回递归之前,需要将y轴的偏移量增加,向上移动1/D,也就是返回去绘制上一层的y轴
plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
def createPlot(inTree):
"""
需要绘制的决策树
:param inTree: 决策树字典
:return:
"""
# 创建一个图像
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
# 计算出决策树的总宽度
plotTree.totalW = float(getNumLeafs(inTree))
# 计算出决策树的总深度
plotTree.totalD = float(getTreeDepth(inTree))
# 初始的x轴偏移量,也就是-1/2W,每次向右移动1/W,也就是第一个叶子节点绘制的x坐标为:1/2W,第二个:3/2W,第三个:5/2W,最后一个:(W-1)/2W
plotTree.xOff = -0.5/plotTree.totalW
# 初始的y轴偏移量,每次向下或者向上移动1/D
plotTree.yOff = 1.0
# 调用函数进行绘制节点图像
plotTree(inTree, (0.5, 1.0), '')
# 绘制
plt.show()
class DecisionTree():
def fit(self, x, y, x_label):
self.label = x_label # x数据集对应的 特征标签
numpy_data = np.c_[x, y] # 把x,y拼接成一个numpy矩阵,方便后面操作
self.tree = self.build_tree(numpy_data) # 构建树
def build_tree(self, numpy_data): # numpy_data n行m列的矩阵,最后一列是结果集。返回字典
finish_columns = np.unique(numpy_data[:, -1])
if len(finish_columns) == 1:
return finish_columns[0] # 返回ng与ok,表面这个分支已经分到叶子了
rows, columns = numpy_data.shape # numpy行数与列数
root_numpy = np.zeros(columns - 1) # 构造全为0的numpy数组,保存信息熵数据
for i in range(columns - 1):
sum = 0
unique_data = np.unique(numpy_data[:, i])
for j in unique_data:
len_whole = len(numpy_data[(numpy_data[:, i] == j)])
len_ng = len(numpy_data[((numpy_data[:,i] == j) & (numpy_data[:, -1] == "ng"))])
len_ok = len_whole - len_ng
if len_ng != 0 and len_ok != 0: # 有一个为0就不用参与计算
x = len_ok / len_whole
sum = sum + round(len_whole / rows * (x * np.log2(x) + (1-x) * np.log2(1-x)), 3)
root_numpy[i] = sum # 保存各个特征的信息熵
root = root_numpy.argsort()[-1] # -1 选取最大值索引。np.argsort():排序后的索引
tree_dict = {self.label[root]: {}}
for values in np.unique(numpy_data[:, root]):
numpy_root = numpy_data[(numpy_data[:, root] == values)]
tree_dict[self.label[root]][values] = self.build_tree(numpy_root)
return tree_dict
if __name__ == "__main__":
data2 = ["青绿", "乌黑", "乌黑", "青绿", "浅白", "青绿", "乌黑", "乌黑",
"乌黑", "青绿", "浅白", "浅白", "青绿", "浅白", "乌黑", "浅白", "青绿"]
data6 = ["蜷缩", "蜷缩", "蜷缩", "蜷缩", "蜷缩", "稍蜷", "稍蜷", "稍蜷",
"稍蜷", "硬挺", "硬挺", "蜷缩", "稍蜷", "稍蜷", "稍蜷", "蜷缩", "蜷缩"]
data3 = ["浊响", "沉闷", "浊响", "沉闷", "浊响", "浊响", "浊响", "浊响",
"沉闷", "清脆", "清脆", "浊响", "浊响", "沉闷", "浊响", "浊响", "沉闷"]
data4 = ["清晰", "清晰", "清晰", "清晰", "清晰", "清晰", "稍糊", "清晰",
"稍糊", "清晰", "模糊", "模糊", "稍糊", "稍糊", "清晰", "模糊", "稍糊"]
data5 = ["凹陷", "凹陷", "凹陷", "凹陷", "凹陷", "稍凹", "稍凹", "稍凹",
"稍凹", "平坦", "平坦", "平坦", "凹陷", "凹陷", "稍凹", "平坦", "稍凹"]
data1 = ["硬滑", "硬滑", "硬滑", "硬滑", "硬滑", "软粘", "软粘", "硬滑",
"硬滑", "软粘", "硬滑", "软粘", "硬滑", "硬滑", "软粘", "硬滑", "硬滑"]
result = ["ok", "ok", "ok", "ok", "ok", "ok", "ok", "ok",
"ng", "ng", "ng", "ng", "ng", "ng", "ng", "ng", "ng"]
x_label = ["触感", "色泽", "敲声", "纹理", "脐部", "根蒂"]
x = np.array([data1, data2, data3, data4, data5, data6]).transpose()
y = np.array(result)
decisionTree = DecisionTree()
decisionTree.fit(x, y, x_label)
print(decisionTree.tree)
createPlot(decisionTree.tree)
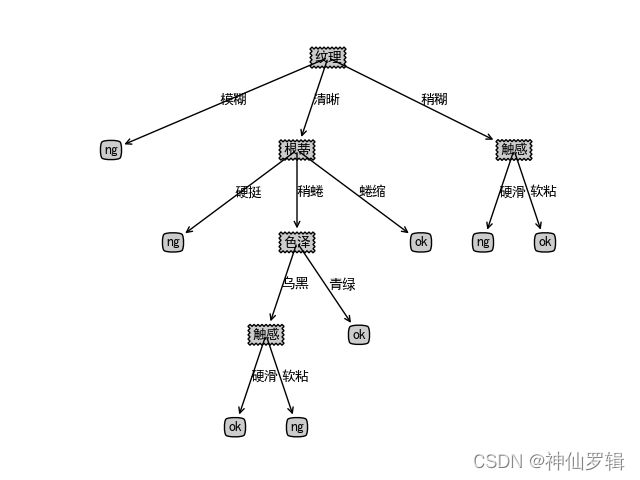
可视化得到图如下:
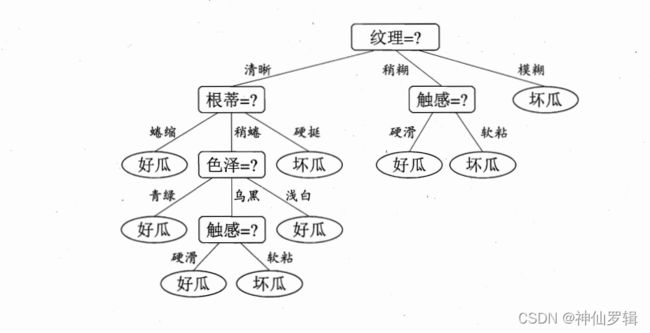
对比西瓜书
对比发现又两点不同
一是 发现纹理-->根蒂-->色泽 这里缺少浅白,这是因为数据集本身就不存在(清晰、稍蜷、浅白)。这里可以进行填充。感兴趣的可以试下。
二是 在纹理为稍糊、触感这里,ng与ok反了,这里是西瓜书打印错误。
最后亿点说明:
为什么构建树的时候只需要计算信息熵就可以了,而且不用移除出之前的特征?
因为我们实际上计算的是
sum = sum + x * np.log2(x) + (1-x) * np.log2(1-x)
这个值我们可以观察下y = x * np.log2(x) + (1-x) * np.log2(1-x)。这个函数关于x=1/2对称
当x属于(0,1)时连续,求导,计算出(0,1/2)递减,(1/2,1)递增
当x = 1/2最小,y越小说明信息增益越小,文章开头讲过。求极限,利用洛必达法则,上下求导就可以算出。当x趋于0时 y也趋于0且连续所以函数曲线大致为可以画出类似于 "- sin(πx)" 在(0,1)。因为结果ok,ng为同一组的时候时不能在分的。当可以再分时,我们前面选出的特征一定是负的最大的。对公式简单处理,就可以快速构造决策树