IFOS3D(一)
IFOS3D
- 1 介绍
-
- 1.1 全波形反演(FWI)
-
- 目的
- 方法
- 从2D到3D
- 1.2 IFOS3D
-
- 概念
- 目的
- 方法
- 2 理论与实践
-
- 2.1 反演问题
-
- 梯度法
- 2.2 使用SOFI3D进行正向建模
-
- 2.2.1 有限差异建模
- 2.2.2 SOFI3D的其他特性
- 2.3反转过程概述
- 2.4梯度计算
-
- 2.4.1单色场的提取
- 2.4.2波场计算
- 2.4.3时域和频域的梯度方程
1 介绍
1.1 全波形反演(FWI)
目的
最大程度地减少建模数据与观测数据之间的误差,从而找到能够最佳解释观测数据的地下模型
方法
通过迭代最小化模型和观测数据之间的不匹配度,来实现地下多参数图像的存储,通常用基于梯度的方法来解决最优化问题
从2D到3D
2D可以降低反演的计算成本,但是,2D近似无法解释3D散射,并且可能导致3D异构介质中出现伪影。3D FWI的使用为反演3D结构和获得地下3D图像提供了可能。通常,用(粘滞)声波方程描述FWI应用中的波传播
1.2 IFOS3D
概念
3D弹性全波形反演工具
目的
解决3D地下的弹性参数(纵波、横波速度和密度)。
方法
它基于共轭梯度法;用时频方法计算梯度;在时域中使用快速有效的有限差分正解器SOFI3D来模拟波场;为了优化梯度方法IFOS3,采用了对角Hessian近似的计算和L-BFGS方法的应用
2 理论与实践
2.1 反演问题
IFOS3D使用的L2-范数的失配函数E,m是能够最佳解释观测数据的地下模型
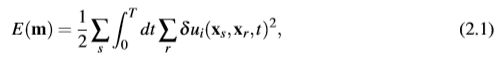
xs:源位置
xr:接收器位置
t:时间
T:整个记录长度
δui:位移残差
uobs:观测数据
u:建模数据。
源位置xs和接收器位置xr的位移残差δui= ui-ui,obs 的第i个分量。平方残差在所有信号源s和接收器r上求和,并在整个记录长度T上随时间t上积分。
梯度法
共轭梯度法
目的:解决优化问题
方法:局部反演
通过在E的最陡下降方向上更新模型来迭代地使失调最小化。迭代k中的模型更新为
![]()
∇mEk:失配函数的梯度
P:预处理算子,它减轻了梯度中的幅度影响
αk:步长
FWI中的失配函数通常非常粗糙,而且包含了局部最小值,为了使用该局部反演方法达到全局最小值,使用共轭梯度。
与一般梯度∇mEk相比,使用共轭梯度ck可以改善收敛。迭代k中的共轭梯度方向有
![]()
ck通过添加先前梯度的一部分稳定反演,标量β用Polak-Ribiere方法估算为
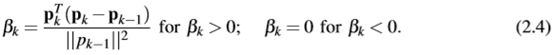
将新模型估算为
![]()
2.2 使用SOFI3D进行正向建模
3D弹性FWI的前向求解器
特点:该求解器可以精确地模拟地震波在弹性介质中的传播。否则,反演结果中的伪影和偏差可能是由拟合波场中的建模误差引起的。
时域有限差分求解器
“ IFOS3D”使用时域有限差分求解器“ SOFI3D”的弹性版本进行波场建模
背景:由于反演过程的特点是前向建模数量众多,因此FWI运行时主要受波形建模时运行时间的影响
特点:它非常有效且快速地求解了3D弹性波方程。该代码离散化了交错网格上弹性波方程的速度应力公式。它能够准确地对3D复杂介质中的波传播进行建模。
波传播
波传播可以用速度应力公式描述。该公式使用质点速度v =∂u/∂t作为波场参数。对于由力 f 引起的弹性各向同性介质波的传播,可以描述为一阶微分方程:
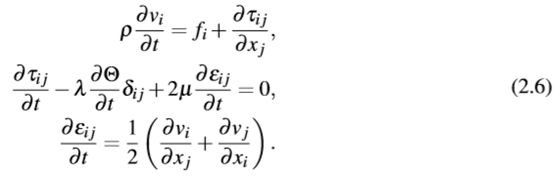
弹性介质由密度ρ和拉姆参数λ和µ来描述
τij:应力张量的元素
εij:应变张量的元素
Θ:应力张量的轨迹
2.2.1 有限差异建模
对于3D弹性波传播的仿真,这些方程式由有限差分(FD)近似。
** 3D交错网格系统**
目的:计算偏导数
方法:将场参数和模型参数离散化在交错网格系统上。
优点:与传统的笛卡尔网格相比,交错网格可在相同精度水平下实现更大的网格间距。导数由中心有限差分近似。
我们使用笛卡尔网格(x,y,z)= (i,j,k)。模型参数λ,μ和ρ以及对角线应力分量σii定位在整个网格点上,而速度和非对角线应力分量是在将网格点移到原始系统的一半网格线上的网格上计算的。
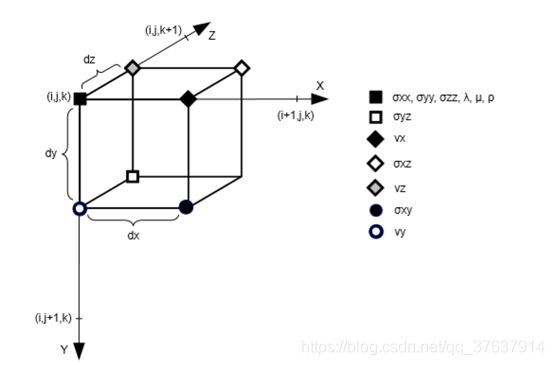
图2.1:用于SOFI3D中的3D FD建模的交错网格坐标系
最简单的有限差分是二阶的,利用网格空间为dh的相邻的两个网格点计算这些网格点之间的导数(dh表示两个相邻网格点之间的空间距离),如下所示

SOFI代码使用二阶时间和二阶至十二阶空间有限差分算符,可以根据问题进行选择。
为了求解方程式2.6的系统,每个时间步长执行两个步骤:
使用空间应力导数计算速度更新,并将其添加到先前的速度值中
使用空间速度导数和霍克定律计算应力值更新,并将其求和到先前的应力值中
因此,所有时间步长上更新值的总和即为速度和应力值的时间导数。
2.2.2 SOFI3D的其他特性
边界条件
有两种方法可以避免来自SOFI3D模型边界的人为影响。通过将振幅乘以一个指数衰减因子,第一波对模型边界区域内的波进行指数衰减。在边界区域至少需要30个网格点的厚度。第二种方法是卷积完全匹配层(C-PML)的实现。与传统的指数阻尼相比,该方法可以提供更好的性能,并且通常10格点厚度的边界区域就足够了。但是,在强烈的对比和模型边界处的异质性的情况下,可能会导致不稳定性。
自由表面
在自由表面,垂直应力分量σxy,σyy和σzy为零。平面自由表面是隐含在SOFI3D中的,采用Levander(1988)描述的镜像技术。
网格分散与稳定性
为了减轻数值分散和网格的各向异性,必须将网格间距选择得足够小。对于四阶空间和二阶时间方案,准则

确保波场误差小于5%(Bohlen,2002)。它取决于最小波长λmin,由最小速度vmin和最大频率fmax定义。高阶FD运算符可实现更大的网格间距。为了确保模拟的稳定性,时间间隔必须满足CourantFriedrichs-Levy(CFL)稳定性准则(Courant等,1967)。它与最大速度vmax有关,由下式给出

泰勒或操作员下订单的常数因素为7 6。对于不同的FDorders和Holberg系数,我们参考SOFI手册。
粘弹性
存在SOFI3D的粘弹性版本。对于它的实现,我们参考Bohlen(2002)。到目前为止,我们仅使用SOFI3D的IFOS3D的弹性版本。但是,应该包括粘弹性更新功能。这使得可以在反演过程中将粘弹性用作被动参数。可以使用IFOS2D成功测试2D弹性FWI。
2.3反转过程概述
图2.2说明了不同的步骤,这些步骤在IFOS3D中的共轭梯度算法的每次迭代中执行。每次迭代可以分为三个部分。首先,计算每个炮弹和模型参数(m)的拟合梯度ΔEk(m)。其次,为了计算搜索方向(ck),将所有镜头的误拟合相加,进行预处理,然后计算共轭梯度ck。第三,执行步长估计,该步长确定更新的总大小。 IFOS3D还可以计算对角Hessian近似值,并可以使用L-BFGS sheme,这将分别在2.10节和2.11节中进行介绍。时变方法实现的共轭梯度方法(Sirgueetal。,2008)。使用有限差分求解器SOFI在时域中执行波场建模,而梯度是在频域中计算的。应用they上的离散傅立叶变换来计算频域场。频域反演的主要优势是仅计算少数离散频率的梯度的可能性(例如Pratt,1999; Sirgue&Pratt,2004; Brossier et al。,2009)。与时域倒置相比,这大大降低了存储成本,而时域倒置通常需要完整的前场存储。时频方法还允许使用高效,快速的3D时域FD前向求解器。因此,对于3D弹性FWI,建议在计算性能方面。
2.4梯度计算
杂散梯度是通过伴随方法计算的,该方法可以从扰动理论中得出(例如Tarantola,1984; Mora,1987)。图2.2中的工作流蓝框给出了其实现的示意图,并显示了梯度作为正向场和共轭伴随场的乘积。 Butzer(2015)给出了IFOS3D中梯度方程的详细推导。在这里,我们将仅简要介绍所采用的方程式,并专注于实现。
2.4.1单色场的提取
对于频域场参数的梯度计算,离散频率需要向前和向后传播的场。我们遵循Sirgue等人的方法。 (2008年),并使用离散傅立叶变换提取单色场,其中nt是时间步数,Δt是时间采样和AI场参数。离散傅立叶变换在y上执行,在每个时间步中对Ai的傅立叶求和求和。因此,不需要存储不同时间步长的时域场。此外,只要仅对很少的频率执行变换,附加操作的数量就很少。因此,可以以较低的额外成本实现从时域到频域的改变。
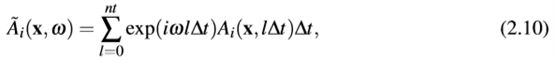
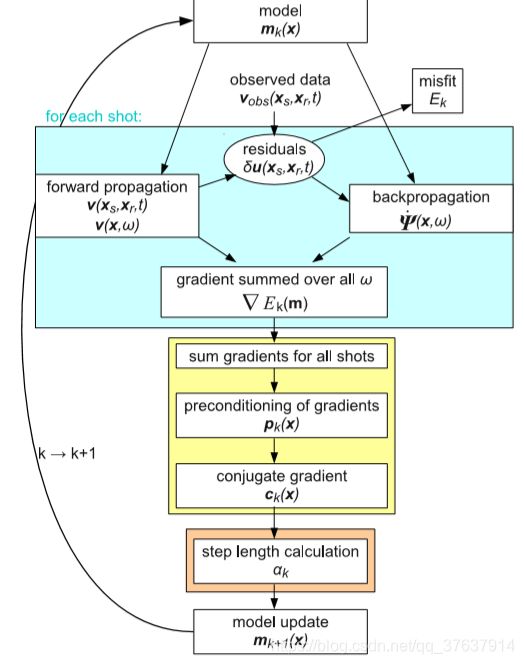
图2.2:IFOS3D的工作流程显示了每个迭代过程中执行的不同步骤。
2.4.2波场计算
第一步,模拟模型mk的正向传播场,该场从源传播到介质。在每个接收器位置存储地震图v(xr,t)。此外,通过应用离散傅立叶变换(等式2.10),我们计算出粒子速度〜v(x,ω),该速度存储着每个离散反转频率和每个网格点的内存。在每个接收器位置,估计时间反向的残余位移地震图δui(xr,T-t0)。此残留物同时从所有接收器反向传播到介质中。相应的反向传播场定义为
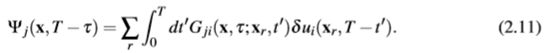
因此,我们使用基于一阶波方程的正向求解器,从而计算出时间导数∂Ψ/∂t=˙。对于反向传播,时间线是反向的,我们计算从时间T开始向后的波场。与前向传播相同,我们提取fl y上的频率场〜Ψ(x,ω)。这些频率场针对每个频率存储在存储器中。
2.4.3时域和频域的梯度方程
最后,将梯度乘以每个频率的正向和共轭联合波场的乘积,并求和所有频率。在下文中,将更详细地描述相应的方程式。在时域中,弹性参数λ,μ和ρ的失配梯度可以估计为正向和反向传播场之间的零延迟互相关(例如,Mora,1987; Butzer,2015)
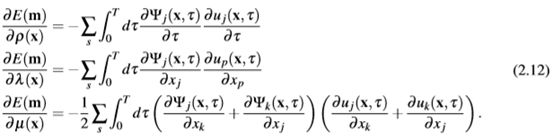
这些方程式可以变换到频域。使用傅立叶变换将时域u(x,t)的场变换成频域〜u(x,ω)并向后变换
![]()
另外,我们使用时域中两个真实信号A和B的零滞后互相关被一个信号与另一个信号在整个频域中积分的共轭信号相乘的乘积所代替。
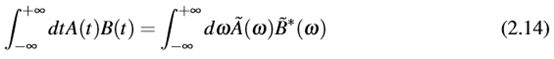
现在将其应用于2.12中的时域渐变表达式。如果满足条件ofu(x,t)= 0和∂u(x,t)/∂t= 0fort <0andt> T,则时间积分RT 0dτ可扩展为R +∞-∞dτ。在密度梯度中,时间导数分别通过乘以系数iω变换到频域。空间导数不受转换的影响。频域中的梯度可以表示为
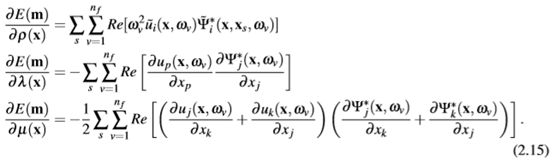
因此,可以替换整个频率上的积分,而无需考虑离散频率上的总和。只要在反演期间连续覆盖波数频谱,就可以在FWI中仅使用很少的频率与全频谱形成对比,例如(例如Sirgue&Pratt,2004; Plessix,2009; Brossier,2011)。但是请注意,在复杂波场的情况下,时域FWI的更好冗余可以导致更好的性能(Virieux&Operto,2009)。
2.4.4实施梯度计算
对于每次发射,根据公式2.15,使用所存储的前向磁场〜v(x,ω)和反向传播磁场〜˙(x,ω)计算梯度。因此,ρ的梯度可以直接作为速度分量〜vi和〜˙i的乘积来计算。根据计算λ和µ的梯度所需的阶跃位移ui和Ψi,频域实现了与
nit ui(x,ω)和Ψi(x,ω)的空间导数是使用限定的公式计算的。
2.4.5地震速度参数化的梯度表达式
IFOS3D将地震速度参数化用于FWI。不同参数类别之间的关系由下式给出
对于vp,vs和ρ0的梯度,我们通过应用链式规则找到
如上节所述,IFOS3D可以验证λ,μ和ρ的梯度。然后,将速度参数化的梯度计算为Lam梯度的线性组合。注意,密度梯度取决于参数设置。
2.5梯度预处理
梯度的幅度受到场的几何幅度衰减的强烈影响。这尤其导致源和接收器周围的高值。如果没有预处理,模型更新将因此集中在源和接收者旁边的区域,并且反演失败。因此,彻底的预处理可减轻梯度中的几何影响,对于成功进行反演具有重要意义。在局部方法中,我们使用以下形式的指数函数
参数r是到源位置(| x-xs |)或接收器位置(| x-xr |)的距离。 Dare的功能由小值相邻的毒药或xr表征,但对于大r值接近。因此,正值a定义D的最小值,而b影响锥角半径。在图2.3中,函数D1和D2绘制了常数a = 1000和不同的值ofb。函数D1允许在整个角度上有一个更平滑的锥度,而函数D2是一个asharperper,它特别适合于非常局部锥度。实际上,后一种锥度通常适合于阻尼接收器的伪像,该伪像通常仅延伸很少的网格点,而D1锥度可用于消除更多的扩展伪像。在IFOS3D中实现了三种类型的局部预处理:-围绕源和接收器位置的球面逐渐变细;-围绕源和接收器平面的锥度;-C-PML边界的锥度
使用D2函数实现C-PML边界的渐缩DPML(x),其中到模型边界的距离用于r。这是必要的,因为FWI倾向于在边界中产生伪像。使用源锥度Ds和接收器锥度Dr,总的预处理梯度可以估算为
图2.3:对于源或接收器位于零距离处的a = 1000的锥度函数D1(a)D2(b),绘制了不同的b值。
2.6计算共轭梯度作为搜索方向
如公式2.2所示,可以将预处理的梯度用作更新模型的搜索方向。但是,使用共轭梯度可以稳定反演并改善收敛。当前迭代的预处理梯度(pk)和前一迭代的预处理梯度(pk-1)和共轭梯度(ck-1)用于根据等式2.3和2.4计算共轭梯度方向。因此,共轭梯度法的应用需要存储先前迭代的预处理梯度和共轭梯度。共轭梯度给出了模型更新的方向,但不包含有关其大小的信息(也涉及其他参数类)。因此,我们将ck归一化为最大值,并将其乘以相应参数类别的参考值(v0 p,v0 s,ρ0):
此外,如下一节所述,执行步长估算。
2.7步长计算
良好的步长计算对于FWI的良好性能至关重要。但是,其估算的运行时间应该很短。 IFOS3D使用抛物线法(例如Kurzmann等,2009)来找到最佳步长,这可以通过合理的计算成本来实现。除当前模型外,还计算了两个测试步长的失配值。为了减轻运行时间,仅对镜头的子集(Ns(步骤))执行此操作。
这三个失配值用于查找抛物线。将其最小值的位置用作模型更新的最佳步长αk。这导致(2×Ns(步))个额外的正向建模。当然,抛物线只是真实失配曲线的粗略近似。因此,成功进行步长估计需要采用其他条件:1.在抛物线极值最大的情况下,我使用误差最小的测试步长2.定义最大步长,不能超过3.如果步长为估计为零或步长为负,使用第一测试步长的较小比例更新模型
测试步长的选择对于该方法的性能很重要。通常,当较大的模型更新确定地下的粗糙结构时,反演开始时的测试步长可能会更大。后来,对于更细的模型结构,需要对模型进行较小的更改。在IFOS3D中,选择初始测试步长(TESTSTEP),并在每个频带的第一次迭代中使用。对于以后的迭代,将使用先前迭代的最佳步长αk,并将新的测试步长确定为αk/ 2。如果新的测试步长大于TESTSTEP,则将TESTSTEP用于下一次迭代。如果新的测试步长小于TESTSTEP的25%,则将其设置为TESTSTEP的25%。注意,对于所有参数类别,估计一个步长。限制另一个参数类的更新可能会很有用。这可以通过在模型更新中应用加权因子来实现。
2.8模型更新
从某个初始模型开始,每次迭代k中的模型都用(-αkck)更新。通常,弹性FWI更新三个参数类(vp,vs和ρ)。针对每个参数类别计算共轭梯度,并使用该参数的平均值进行缩放,以考虑这些参数相对于其他参数的大小。但是,请注意,所有参数仅估算一个步长。限制一个参数类相对于另一个参数类的更新可能很有用。这可以通过在模型更新中应用其他加权因子来实现。
2.9完整版本转换过程
全波形反转是一个迭代过程。我们通过沿失配函数的最陡下降方向更新模型参数以使其达到最小值来搜索最佳模型。但是,地震数据的反演通常是高度非线性的,失配函数不是平滑函数,而是包含许多局部最小值。使用像共轭梯度法这样的局部反演方法,可能会使局部最小值最小化。在这种情况下,可以通过倒置模型相对较好地解释观察到的数据,但是模型结构不正确。为了找到真实的地下模型,起始模型的选择和不同的反演策略很重要。
2.9.1起始模型
起始模型的选择对于FWI至关重要。初始模型应包含有关地下的初步信息,尤其是对于复杂数据。使用平稳的启动模型可能会很有用,因为界面的强烈对比和结构难以通过FWI进行更改。起始模型应该已经大致解释了低频数据,因此不会出现跳周期问题。这意味着,启动模型所需的平滑度取决于低频数据的可用性。
2.9.2多规模反演
不必一次反转整个数据集,而是从一部分数据开始并在反转的不同阶段添加更多数据,这非常有帮助。
通常有三种不同类型的数据可供选择:1.频率滤波:倒相从低频数据的反演开始,然后增加更高的频率; 2.时间窗:第一步是将到达的第一步反相,然后是更多数据 在稍后的阶段中添加3.偏移窗口:单独的长偏移和短偏移数据反转策略的选择取决于数据集和问题的复杂性,并且不同策略的组合也可能有用。
在IFOS3D中,只有第一种策略,此时可以进行频率过滤。
在下文中,我们将更详细地说明此方法。
2.9.3频率级
IFOS3D根据少量单色频域场计算梯度。由此,将反转细分为不同的频率级,这些频率级使用不同的频率集。 FWI中的一种常见技术是从低频开始,对较大规模的地下结构进行反演,然后将较高的频率包括在内,以找到更精细的模型结构。图2.4证明了这一点,Bunksetal。,1995。绘制了针对不同标度长度的功能差,这些标度从a)增大到e)。随着规模的增加,频率的降低,失配函数变得更加平滑,局部极小值的数量减少。因此,要达到全局最小值,对于低频而言,模型可能离实际模型更远,而对于高频,则需要更接近的模型。查看数据时也可以理解这一点。建模数据和观测数据之间的相位差必须小于半个周期,以便可以将相位正确地分配给彼此。否则可能会发生循环跳跃,并且反转可能会以局部最小值结束。对于较低的频率,此条件更容易填充。因此,FWI中的多尺度方法可以减轻周期跳跃的问题,并有助于达到全局最小值。
图2.4:从头到脚逐渐增加刻度长度的功能失调的图示[来源:Bunks等。(1995)]。
选择频次在多尺度反转中包含更高的频次。 Brossieretal。 (2009年)测试了三种不同的方法:•顺序方法:一次使用一个频率进行单频反转•双层方法:从一个低频开始,每级增加一个更高的频率,因此每级频率数量增加•同时方法:在每个阶段将一组通常为3-5个频率反转,重叠的频段总体而言,他们发现多个频段同时反转的最佳性能,并且在其反射几何应用中具有重叠的频段。因此,较低的,已经转换的朋克频率中的频率的夹带似乎无法改善反转。当使用五个频率而不是一个频率阶段的三个频率时,Pratt(1999)也显示出改进的性能。因此,尽管成功的应用表明单频倒置是可能的,但是更高的频点可以改善倒频,而单频方法似乎并不令人满意。幸运的是,使用每级频率少的频率组代替时频FWI中的单个频率不会增加太多的计算成本。相反,在使用频域前向求解器时,需要额外模拟这些频率。
频率间隔
频率间隔的选择需要确保连续覆盖波数频谱。 Sirgue&Pratt(2004)表明,当不仅考虑一条迹线而且考虑一定范围的偏移量时,对于频率间隔来说通常可以满足1 / T的采样间隔(T:时间序列的长度)。由此,较大的偏移使得能够以较低的频率采样覆盖波数频谱。对于简单的一维模型,可以使用以下公式计算相关频率:
其中αmin取决于偏移量与深度的比率,对于较大的最大偏移量而言较小(Sirgue&Pratt,2004)。尽管如此,使用附加频率仍会增加数据的冗余度,这通常会改善图像质量,尤其是在反演的非线性度较高的情况下。
2.10用对角Hessian近似进行预处理
在2.5节中,我们讨论了一种非常简单的预处理方法,该方法可以局部衰减源和接收器周围的梯度。
这种方法对于简单的问题非常有效,例如在传输几何中经常发现的问题。
但是,在复杂的场的情况下,这种方法是不够的。
如果我们看一下表面的几何形状,我们会发现梯度非常集中在表面附近,在该表面上,大部分能量传播。
这意味着如果不通过预处理进行增强,则不会更新更深的模型零件。
IFOS3D提供了采用对角线Hessian近似进行预处理的可能性。
这种方法考虑了有关失配函数的二阶导数(Hessian)的信息,是一种物理资助的方法。
Hessian的对角元素可预测梯度中包含的几何幅度扩展,因此可用于发现梯度的改进的空间缩放比例。
在地表地震中,使用Ha的对角线元素进行梯度缩放会增强模型更深部分的影响。
在下文中,我们将对实现进行概述。
有关Hessian在FWI中的作用的其他信息,请参阅Pratt等。
(1998); Virieux&Operto(2009); Brossier(2011)和Butzer(2015)。
2.10.1
完整的牛顿法使用Hessian marixH进行模型更新,由
在线性反演问题的情况下,用δm更新将导致一步之内失配函数的最小值。像FWI这样的非线性反演问题会逐步线性化并迭代地逼近最小值。与梯度法相比,牛顿法的收敛性仍然大大提高。相对于模型参数,Hessian是misfit函数的二阶导数:
变量n表示模型参数的数量。 H的大小为n×n很大,因此其显式计算非常昂贵。对于像3D弹性FWI应用程序这样的大型FWI问题,这是不可能的。仍然可以通过使用有关Hessian的一些信息来改进梯度方法。将梯度法(方程式2.2)的模型更新与牛顿更新进行比较,梯度法将H近似为αP。通过用对角线Hessian的近似值对梯度进行预处理,可以改进梯度方法。
2.10.2理论
对角Hessian近似的计算
基于L2范数的错配函数(方程2.1)的二阶导数可以表示为
在下文中,我们忽略了包含二阶偏导数场并约束第一项的第二项Rjl,即所谓的“近似Hessian”(Ha)jl。它是在所有源s和接收器r上求和的一阶偏导数场的零时滞互相关计算出来的。对于IFOS3D中的预处理,我们仅使用对角线元素并计算离散频率的元素(Ha)jj。然后将公式2.25转换为(Butzer,2015)
伴随梯度法不能直接计算偏导数场,也称为Fr’echet导数核,现在是估计元素(Ha)jj所必需的。频域中关于弹性参数λ,μ和ρ的导数可表示为(见Butzer(2015))
术语Gji(x,ωv; xr,0)表示格林的接收器函数频率为离散频率,并乘以前向场。与梯度计算相同,我们使用链式规则将这些方程式转换为地震速度参数化
Hessian预处理
作为针对不同参数的预处理算子(Pρ(x),Pλ(x)和Pµ(x)),我们使用Ha的对角线的倒数,这对角线矩阵很简单:
系数ερ,ελ和εµ是水位,出于稳定性考虑,将它们加到Hessian近似中。否则,在非常低的波幅范围内的Ha中很小的元素会导致这些区域中梯度的强烈增加,从而可能导致伪影。
2.10.3 Hessian预处理的实现
图2.5说明了IFOS3D中Hessian预处理的实现。请注意,Hessian计算取决于采集几何和当前模型mk,但不包含有关真实地下模型的信息。
波场计算
场的正向传播和单色频率场(v(x,ω))的提取已在梯度计算的框架中进行(第2.4节)。主要的额外计算工作是花费在格林接收器函数Gji(x,ωv; xr,0)的计算上。与梯度计算不同,在反向计算中,反向传播的波场同时从所有接收器传播,格林的完整接收器功能集要求每个接收器和每个分量进行一次传播,从而产生3×Nrec个额外的波场模拟(Nrec:接收器总数) 。我们通过使用重力阶跃函数(Θ)和力-时间函数(定义为
δ(t-tstep)函数为其导数相同的时移tstep用于正向信号源。为了估算格林在频域的接收器函数,我们对y上的函数Gij(xr,t; x,tstep)进行了离散傅里叶变换(方程2.10)。对于每个离散频率和每个接收器,函数Gij(xr,ωv; x,0)存储在存储器中。由于高的计算运行时间和存储需求,我们在这里采用两个近似值。首先,我们只使用一部分接收器。其次,我们仅计算格林接收机函数的分量,该分量对应于前向场的来源,因此仅计算偏导数场的一个分量。这些限制仅对预处理最重要的源附近的梯度校正产生很小的影响。但是,必须对较小的接收器伪像进行额外的本地预处理。
图2.5:在IFOS3D中实现的在迭代k处计算Hessian预处理运算符的工作流。
Hessian计算
对于每次发射,根据等式2.27和2.28,将前场与每个频率的每个格林格林接收机函数相乘来计算偏导数场。
因此,将前向场的速度与(iω)-1进行积分,以找到位移场,并利用四阶有限差分计算空间导数。将偏导数场与它们的复共轭相乘,然后在所有频率和接收器上求和,最后在所有镜头上求和,以求出vp,vs和ρ的对角Hessian近似(方程2.26)。
预处理
最后,可以根据方程式2.29计算预处理算子并将其应用于梯度(P(x)∇Ek)。目前,尚未实现对水位ε的自动估算,而是从输入文件中获取水位。因此,需要使用当前迭代的梯度和Hessian对ε及其对梯度预处理的影响进行经验尝试。
围绕接收器位置以及在C-PML边界中应用了梯度的附加局部阻尼。
完整版本转换过程
在每个频率阶段开始时,都会对Hessian预处理运算符进行一次计算。它在整个阶段都适用。不幸的是,目前尚未自动估计出水位ε。这就是说,实际上,在反演开始新的频率阶段之前,需要对梯度和Hessian进行估算,并凭经验确定水位。这导致每个频率级的第一个梯度的额外计算。除了Hessian预处理运算符的计算和应用外,诸如梯度归一化,模型更新和步长计算之类的反演过程保持不变。
Hessian预处理的成本
每个频率级都会计算一次Hessian预处理运算符。 Green接收器功能的建模主要需要额外的运行时间,其数量与用于这些计算的接收器子集相对应。另外,只要需要在每个频率级之前根据经验确定ε,就执行一次额外的梯度计算。总之,与使用完整的Hessian矩阵相比,得出以下近似值:
•仅使用Ha的对角元素
•仅使用一部分接收器进行计算
•通过仅反向传播一个分量δ来仅部分导数场的一个分量δ -脉冲
•每个频率级仅估计一次Hessian。
2.11 L-BFGS方法
本节介绍以BFGS方法开发人员命名的L-BFGS(低内存BFGS)方法,即Broyden,Fletcher,Goldfarb和Shannon。该方法属于准牛顿方法的类别,在IFOS3D中实现为反演过程的优化。上一章简要介绍了Hessian运算符和Newton方法。拟牛顿方法不是直接计算逆Hessian H-1 k,而是通过使用迭代中的梯度变化来近似(逆)Hessian。从初始的Hessian近似值H0开始,在每次迭代中更新(逆)Hessian的近似值,以找到对Hessian的更准确的估计。
逆Hessian对梯度作用的应用是由于有限带宽效应和几何幅度效应对梯度的反褶积(Pratt等,1998; Brossier等,2009)。Brossier等人的2D FWI先前申请。(2009)和Brossier(2011)与传统的共轭梯度法相比,使用L-BFGS方法显示出更高的收敛速度和更清晰的图像。另外,可以实现多个参数类别的正确求逆,而无需对不同参数类别进行经验加权。
2.11.1 BFGS和L-BFGS方法的理论
利用梯度的变化γk=∇Ek+ 1−∇Ek和模型变化sk = mk + 1−mk,BFGS条件被公式化为(Nocedal&Wright,1999)
从初始猜测H-1 0开始,每次迭代都更新逆Hessian近似,而无需显式计算二阶导数。但是,由于Hessian矩阵的尺寸很大(n×n),因此不适用于大量的模型参数。相比之下,L-BFGS方法并未明确存储Hessian矩阵,而是仅使用了最近m次迭代的梯度和模型变化,并在每次迭代中新计算了逆Hessian。对前m个迭代重复应用公式2.30可得出以下公式(Nocedal&Wright,1999):
H-1 k0是初始逆Hessian近似值,允许它随迭代而变化。
2.11.2 L-BFGS更新
L-BFGS方法可以在FWI中非常有效地实现。在IFOS3D中,我们应用Nocedal&Wright(1999)描述的递归算法,该算法在不直接形成逆Hessian逼近的情况下估计乘积H-1 k∇Ek。可以写成
该算法在每次迭代中执行一次,如果选择对角线H-1 k0,则由(4mn + n)个乘法组成。 L-BFGS算法需要额外存储(2mn + m)个用于γγ,sandr的浮动数。因此,可以在运行时以相对较低的额外成本执行合理数量的L-BFGS方法。通常,使用5到20之间的值。在第一个(m-1)迭代中,结果与BFGS方法相对应。
2.11.3 优化的FWI工作流
Hessian预处理和L-BFGS
遵循Brossier(2011)的方法,我们通过使用以对角Hessian近似为前提的梯度变化来应用L-BFGS方法。 Hessian预处理(第2.10节)已经提供了改进的梯度缩放比例。通过另外使用LBFGS算法,可以将非对角折线软梯度记入帐户。此外,在每次迭代中都计算L-BFGS方法,而对角Hessian矩阵每个频率级仅估算一次。当使用预处理梯度时,可缩放的恒等矩阵(Nocedal&Wright,1999)足以作为黑森的初始猜测:
参数归一化
共轭梯度不提供有关不同模型参数相对于彼此的更新的信息。当采用黑森州帐户的非对角元素时,此情况会更改。 L-BFGS方法可以通过添加有关Hessian的非对角元素的信息来改善多参数反演。为了实现不同参数类的无量纲L-BFGS框架,我们使用Brosier(2011)建议的一些代表性模型参数vp0,vs0和ρ0来标准化反框架。
这导致对计算为的梯度进行归一化
和由给出的Hessian近似的归一化
L-BFGS算法计算归一化模型更新,需要通过与代表性模型参数相乘来对其进行归一化:
对于所有参数类,这种无量纲的倒置都能实现易于理解的L-BFGS算法。
工作流程概览
优化的FWI反演的工作流程可以描述如下:
对每个频率阶段
•为每个迭代中的归一化参数计算对角Hessian近似值(Hˆ vp a,Hˆ vs a,Hˆρa)
•计算归一化参数的梯度
•对斜率应用对角Hessian近似值
•保存预处理梯度和模型中的更改,丢弃更小的km km -BFGS算法查找归一化模型更新
•去归一化模型更新•步长计算:首先尝试步长α= 1
•模型更新
牛顿法通常会计算绝对模型更新,对于线性化牛顿法,预期步长接近1。准牛顿LBFGSsheme也是如此。如果将Hessian的近似值很好地达到接近一步的长度,将是有利的。可以如第2.7节所述应用步长估计,测试步长为0.5和1。如果L-BFGS sheme工作良好,则步长接近1会在激活后提示。请注意,在说明中,反演对应于采用Hessian预处理的梯度方法。
3入门
3.1要求
IFOS3D在不同的Linux平台上进行了测试。要运行IFOS3D,需要MPI实现(下面列出的三个)和C编译器。使用Suse Linux和OpenMPI在本地工作站上测试了代码。另外的应用程序是在Juelich(德国)的JUROPA和JURECA超级计算机上以及在德国斯图加特HLRS的Hermit超级计算机上进行的。为了正确运行和处理数据,应在计算机上安装以下程序。这些要求类似于正向求解器SOFI3D。
3.2安装-文件夹结构
解压缩软件包(例如tar-zxvfifos3D.tgz)并切换到目录ifos3D(cdifos3D)后,您将找到不同的子目录:
bin
该目录包含所有可执行程序,例如ifos3D和naspmerge。这些可执行文件是使用命令make 生成的(请参见下文)。
doc
该目录包含有关软件的文档(本用户指南)。
mfiles
存储一些Matlab例程(m文件)。它们可以用于数据的处理和可视化。
par
此目录包含以下文件夹:
•输入和输出:包含IFOS3D参数的输入和输出文件
•源:源参数•接收器:接收器位置
•su:地震图输出文件•支持:观测到的地震图
•模型:模型输入和输出
•grad:梯度输出
•hess:对角粗麻布输入和输出
scripts
在这里,您将找到用于在群集计算机上提交建模作业的脚本示例。
src
该目录包含完整的源代码。附录A中列出了不同的子程序。
libcseife
libcseife库用于过滤地震图
3.3汇编
要编译ifos3D,请更改到par目录并执行make。 Makefile将首先编译外部libseife库,然后编译主程序。在某些情况下,有必要删除libseife目录中的* .d文件。如果出现编译问题,请打开libseife目录,并调整系统的编译器选项。
要更改编译器选项,请在src目录中打开Makefile。在这里,您还可以找到过去使用过IFOS3D或SOFI3D的不同系统上的编译器选项示例。
3.4运行IFOS3D
要使用OpenMPI启动程序,可以使用命令mpirun-np8nice-19 …/ bin / ifos3D。/ in和out / ifOS3D toy.json | tee./in和out / ifos3D.out,该命令在8个处理器上运行IFOS3D最低优先级。标准输出被写入/ in和out / ifos3D.out。您也可以使用shell脚本par / startIFOS3D.sh。对于3D FWI应用程序,在高性能计算中心中使用超级计算机通常很有用。在目录脚本中可以找到一些作业脚本的示例。
4输入和输出
4.1输入文件-*.json
在下面,我们将描述IFOS3D的输入参数。逐字记录的文本显示了它们如何在in / out / ifos3d inv中显示所有parameters.json。还有一个注释的json文件:in / out / ifos3d inv所有参数commented.json。用于波场模拟的参数大部分类似于SOFI3D的参数,并且在SOFI手册中也有描述。
4.1.1网格及其分解
网格
笛卡尔网格系统由每个方向(NX,NY,NZ)上的网格点数量和输入文件中选择的网格点DX,DY,DZ之间的距离指定。这里用NY和DY表示垂直方向。网格间距需要满足色散准则(手册前面有对应理论),至少达到反演中使用的最大频率和最小波长。如果源小波的频率范围违反了色散准则,则在模拟开始时给出警告。
区域分解
并行化是基于区域分解的。每个处理器对整个网格系统中的一小个子卷执行FWI算法。NPROCX,NPROCY和NPROCZ定义了每个方向上的处理器数量,它给出了NPROCX×NPROCY×NPROCZ处理器的总数。注意,每个方向上的处理器数量必须是这个方向上网格点数量的一个公共因子。
4.1.2 FD模型参数
FD操作顺序
用于压力和速度更新的空间FD-sheme的顺序可以是FDORDER=2、4、6、8、10和12。这些顺序导致不同的分散性和稳定性标准(第2.2.2节)。FD阶数越大,网格间距越大,但在强非均匀性的情况下,FD算子越小,精度越高。使用FDCOEFF选项,用户可以在Taylor(FDCOEFF=1)和Holberg(FDCOEFF=2)FD系数之间切换。在CPML边界内,自动应用四阶算子。我们也会使用四阶算子来计算波场速度的空间导数,这是梯度计算所需要的。IFOS3D使用二阶时间离散化。
时间步进
TIME定义总模拟长度。必须选择时间步长DT以满足稳定性标准(SOFI3D最小值),因此取决于网格间距和最大速度。如果违反,IFOS3D将发出警告并终止。反演的步数是由TIME/DT给出的
4.1.3 Sources
小波
模型有不同的小波可以选择
源文件中定义的所用中心频率f和源小波的时延。不同小波和相应光谱的示例图可以在SOFI3D手册中看到。注意,对称Ricker小波是延迟的,其最大周期在一个周期后的源位置被激发。阶跃函数用于计算对角Hessian近似。
如果要定义自己的小波,您可以在源代码src/wavelet.cor 或将SOURCESHAPE=3,并从SIGNAL_FILE中读取外部小波。该文件应包含ASCII格式的源信号,具有正确的时间采样和每行一个采样,如
资源格式
你可以选择一个爆炸源(SOURCE_TYPE=1)激发压缩波或一个指向x,y(垂直)或z(SOURCE_TYPE=2,3,4)方向的点力。SOURCE_TYPE
=5的情况下,也可以使用角度ALPHA和BETA来定义任意方向的力。这在SOFI手册中有说明。平面波激励(SOURCE_REC=2)尚未在IFOS3D中进行反演测试,但也可以在这里进行选择。
4.1.4 模型
模型输入
弹性地下模型由纵波速度vp、横波速度v和每个网格点的密度ρ参数化。模型参数是前向建模和反演的起始模型。有两个选项可以读入模型参数:
READMOD=1:外部模型的模型参数是从定义为MFILE的模型文件读入的,例如toy.vp、toy.vsandtoy.rho放在文件par/model中。在这些文件中,每个材料参数值必须保存为32位(4字节)本机浮点。速度必须以m/s为单位,密度值以kg/m3为单位,在每个网格点定义。这些值是在src/readmod.cand读取的,您可以查看此源代码中参数的正确顺序。READMOD=0:也可以在程序中动态生成模型参数。相应的C函数,例如src/Makefile中包含的src/hh.C。
粘黏性
反演代码仅在弹性版本(L=0)中测试。然而,软件包中包含了SOFI3D的粘弹性变形,可用于正演建模。在这种情况下,速度的弹性更新函数需要替换src中可用的粘弹性更新函数。粘弹性参数不含反演程序,只能作为被动参数使用。有关粘弹性的更多信息,请参阅SOFI手册。
4.1.5 边界条件
Free Surface
如果自由曲面=1,则使用(Levander,1988)提出的绘图方法在全局网格顶部应用平面应力自由曲面。如果FREE SURF=0,则模拟整个空间。
模型边界
该模型在波场衰减的每一侧都包含一个由波脊点组成的边界层。IFOS3D中包含两个选项:
ABSTYPE=1:IFOS3D提供使用卷积完全匹配(C-PML)层来在模型边界中放大波场。这项技术显示出很好的去除模型边界反射的能力。利用FPML参数和边界附近的VPPML参数计算了C-PML系数。对于C-PML技术,宽度FW=10网格点通常就足够了,有时PML边界会产生不稳定性,特别是在该区域存在强模型不均匀性的情况下。有关更多信息,请参阅SOFI手册。
ABSTYPE=2:防止模型边界反射的“传统”方法是exponential阻尼。这种技术非常健壮,但效率较低。厚度至少为30个FW。对于参数DAMPING,您可以使用大约8%。注意,更高的值会导致边界界面反射。周期性边界条件(BOUNDARY=1)取自SOFI3D。它尚未在IFOS3D代码中测试,需要在使用前完全实现和测试。
4.1.6 地震记录输出
在每次迭代和每次拍摄中,IFOS3D存储地震记录。
参数SEISMO定义输出:
0:无地震记录
1:粒子速度(x-,y-和z分量)
2:压力
3:旋度和div
4 : everything
对于IFOS3D的反演,我们通常输出粒子速度(每个组件一个文件),可用于查看波形的拟合。压力场的反演没有用IFOS3D进行测试。有关旋度和div输出的更多信息,请参阅SOFI手册。
接收器位置
接收器定义地震记录输出的位置。它们始终位于网格点上(无插值),如果需要,它们将移动到最近的网格点。注意,这会细化垂直方向。在IFOS3D中定义接收器位置有三个选项:
如果选择READREC=1,则从REC_FILE读取接收器。这个ASCII文件使用x-、y-和z坐标(以米为单位)在一行中定义一个接收器。可以通过使用REFREC定义的参考点来移动接收器位置。
第二个选项(READREC=0)定义接收器的直线,如水平或垂直剖面。此配置文件由其起点(XREC1、YREC1、ZREC1)、终点(XREC2、YREC2、ZREC2)和接收器之间的距离(NGEOPH)定义。
最后一个选择(READREC=2)对3D-FWI非常有吸引力,因为它定义了对3D合成FWI应用非常有用的地震阵列。可以在不同的深度定义多个水平井阵列(REC_ARRAY)。上平面是一个REC_ARRAY_DEPTH的垂直面,距离下一个接收平面有一个REC_ARRAY_DIST的垂直距离。接收器之间的水平距离由DRX和DRY定义。注意,接收器在距离吸收边界10个网格点的距离内排列。
地震图
对于地震记录输出,每个样本从FD建模的时间步骤ndt移位开始写入文件。文件格式可以选择SEIS_FORMAT:
1:SU(本地4字节浮点(PC上的IEEE)/PC上的little endian)
2:TEXTUAL(本地ASCII)
3: BINARY(PC上的IEEE-4字节浮点/PC上的little endian)
我们建议使用SU格式。此格式在每个跟踪前面存储一个头,其中包含时间采样、源和接收器位置以及tracenumber等信息。Seismic Unixoffers提供了不同的SU文件数据处理功能。地震记录存储在foldersu中的每个组件、每个炮点和每个迭代中。SEIS_FILE定义了文件的名称,例如cal_toy_vx_it3.su.shot2
快照
它也可以存储波场的快照(SNAP>0),这意味着波场在整个卷中存储一系列时间。由于存储了大量的数据,这种输出在完全反演中通常没有用处。但是,它可以用于正演建模。也可以保存反向传播波场的快照,但是在这种情况下,函数snap()需要包含在反向传播的时间循环中。有关保存快照的不同选项以及快照的处理(合并和可视化),请参阅SOFI3D手册。
4.1.7正演模拟与反演
使用METHOD=0 IFOS3D执行类似于SOFI3D的正向模拟。对于综合测试,此选项可用于创建“真实”模型的观测数据。对于此选项,存储的地震记录分别存储在每个包含接收器的处理器上,并作为所有处理器的合并文件存储。这样,数据就可以直接用作the FWI中的观测数据。
如果选择METHOD=1,IFOS3D将执行由输入文件中的以下参数指定的共轭梯度FWI。
4.1.8 一般反演参数
参数ITMIN和ITMAX定义了 IFOS3D执行的总迭代次数。每个反转从ITMIN=1开始。但是,可以在第一步中分割反转部分并使用ITMIN,ITMAX=(1,15),然后通过选择ITMIN,ITMAX=(16,30)继续。
该方法只对离散频率进行梯度计算,可作为IFOS3D反演的自然滤波器,而对失配进行时域计算,得到完整的波形。因此,使用滤波地震记录是合理的。选择FILT=1时,IFOS3D用四阶Butterworth滤波器滤除当前迭代阶段最大频率以下的震源子波和观测地震记录。这样就可以计算到最大反演频率的数据的失配。
参数FMAX定义了一个反演阶段中使用的最大频率数。
参数(TAST)定义了通过离散傅里叶变换提取单色频率波场的时间采样。用于计算采样率的周期对应于1/fmax,其中fmax是当前频率的最大频率。一般情况下,对于离散Fourier变换不需要使用小FD时间采样,可以节省运行时间。但是,当用于discrete FD变换的时间步数太少时,渐变看起来是像素化的。因此,建议使用此选项时能够检查渐变。
参数VP0、VS0和RHO0是用于不同参数类的参考值,例如起始模型的平均值。它们用于共轭梯度法的模型更新和L-BFGS法的参数归一化。
可以对每个参数类使用加权因子(WEIGHT)。值1.0表示参数已完全更新。值0.0对应于不更新此参数。这使得可以对不同的参数
4.1.9 观察数据输入
反演需要从foldersuobs中读取的观测或测量数据作为输入。这些数据需要:
采用SU格式;
提供IFOS3D中使用的相同时间采样和时间步数;
标记为(SEIS_OBS_FILE_vx_it1.su.shot2)可以在内部和外部观测数据输入之间进行选择:
EXTOBS=0观测数据是IFOS3D正演模型生成的数据。在这种情况下,数据已经存储在每个处理器的单独文件中,在反转过程中可以由相应的处理器直接读取。每个处理器的文件名是由处理器号扩展(例如obs_toy_vy_it1.su.shot4.5)。注意,在正演建模和反演中必须使用相同数量的处理器。
EXTOBS=1观测数据是从所有处理器的一个文件中读取的。在这种情况下,ifos3d在开始反转之前分割数据,并将其保存为每个处理器的单独文件。使用此选项时,地震记录的顺序必须与接收器文件中接收器的顺序相似。
4.1.10 梯度
梯度输出
计算每个炮点的每个参数类(vp、vs和ρ)的基于L2范数的数据失配梯度,并在所有炮点和使用频率上求和。在每次迭代中,原始梯度以foldergradin二进制格式存储在每个网格点上。值的顺序将组装模型文件中的顺序。它们的文件名包括输入文件(grad file)中给定的标签、此迭代的最大反转频率、参数类和操作数(例如grad/toygrad.vp200.00Hzit6)。此外,共轭梯度被存储。它们被标记为数字迭代2000(例如grad/toy-grad.vp_200.00Hz_it2006)。通过在src/ifos3d.cs源代码中的所需位置包含函数outgrad()可以保存额外的渐变。这有助于观察单次放炮时的梯度或测试预处理功能。
梯度预处理
选项DAMPTYPE2.5节中描述的定义了源位置和接收位置梯度的局部预处理。以下选项可用:
0:无阻尼
1:接收器周围的高斯锥化
2:源和接收器周围的高斯锥化
3:源和接收器平面的高斯锥化除此之外
还应用PML边界的锥化。如果预处理不足以满足渐变,则可以更改锥化参数insrc/precgrad.c。
4.1.11 步长计算
使用第2.7节所述的抛物线法进行步长计算。为了避免计算的长运行时间,仅使用NSHOTS_STEP的子集来估计最佳步长。参数TESTSTEP定义在每个频率级的第一次迭代中使用的初始测试步骤长度。在以后的迭代中,该测试步长根据反演过程进行调整。对于共轭梯度反演,约为0.02的值为
一般来说是个不错的选择。这意味着对于步长估计,测试平均模型参数的2%和4%的更新,并且最大模型更新5%是可能的。
4.1.12 模型输出
模型更新后,将每个网格点的模型参数写入到文件模型中。每次迭代中为每个参数(vp、vsandρ)编写一个文件。二进制文件的结构类似于渐变输出。文件名用MOD_OUT_FILE标记(例如model/toy.vsit6)。
4.1.13 工作流程
工作流文件(in_and_out/workflow.dat)组织不同的反转阶段。图4.1给出了一个检验实例。每行定义一个频率级。这包括每个阶段的迭代次数、频率数和这些频率的列表。我们还没有包含中止标准,因此一个阶段中的迭代次数是一个固定值,并且对应于工作流中给定的迭代次数的最大值。请注意,一个阶段中使用的最大频率数在*.json中定义为NFMAX。IFOS3总是开始读取上面一行。当反转被拆分时,上排必须与当前频率级相似。工作流中包含一些参数,这些参数在FWI中很有用,但在IFOS3D中尚未实现。这些参数包括时间和偏移窗口以及中止标准的参数。它们将被列入今后的工作。
4.1.14 Hessian
如果在输入文件中选择了选项HESS=1,则应用对角Hessian近似对渐变进行预处理。如果已经计算了Hessian近似值,则可以从文件中读取(READ_HESS=1)。在此,从folderhess中读取hessian近似。使用在当前频率阶段开始时写入的文件,标记为形如hess/toyhess.vp200.00hzit11 当新频率阶段以迭代11开始时。READ_HESS=0对角线Hessian近似在IFOS3D中计算,如第2.10节所述。
由于运行时和存储,建议仅使用它的计算接收器。REC_HESS目前尚未完全实施,因此必须将接收器文件或接收器阵列中的距离更改为其双值或三值。
用于计算预处理矩阵(等式2.29)的水位(WATER_HESS)可以根据第一次迭代的梯度和对角Hessian矩阵估计。它不是直接在IFOS3D中计算的,这就导致了在一段时间内不可能进行完全反演,但反演需要分成不同的阶段。
对角的Hessian矩阵存储在文件hessan中,名为e.g.hess/toyhess.vp200.00Hz_it11。在每个频率阶段开始时计算,并在该频率阶段内应用。
4.1.15 L_BFGS
如果BFGS=1,则按照第2.11节所述采用L-BFGS法。L-BFGS 法只能与Hessian预处理(HESS=1)结合使用。到目前为止,L-BFGS方法只适用于地震速度,而不适用于密度。反向参数类的数目(NUBPAR)因此可以被选择为1(VP)或2(Vp或vs)。L-BFGS算法根据梯度变化和前一个BFGSNUM迭代模型估计Hessian
4.2 IFOS3D 输出
4.2.1 ifos3D.out
反转过程可以在文件in_and_out/ifos3D.outwrited中由第一个处理器(MYID=0)执行。这个文件提供了有关IFOS3D中使用的参数、网格分散性和代码稳定性的信息。可以查看不同子程序的正向建模和输出过程。如果程序提前终止,可以检查此文件是否有错误消息。
4.2.2 ifos3D_invers.out
在运行期间,不匹配值和步长信息的输出将写入nandout/ifos3Dinvers.out。每次迭代给出的以下值显示了转换过程:
•当前迭代中定义的参数:参数cdf(在每个反演阶段的第一次操作中设置为一个),此迭代中使用的最低频率和此阶段的频率数。
•每个炮点(L2)的失配值(时域)、炮点总数(L2all)和步长计算中使用的失配值(misfit[0])
•用于步长估计的测试步长(步长)和由此产生的L2不匹配
•步长抛物线和由rc/steplength.c给出的可能警告
•用于模型更新的“最佳”步长和此步长的估计不匹配
•新的测试步长
如果发生反演中的新测试步长问题,这将成为一般在其收敛性和求解问题时很快就可以看出最优步长。