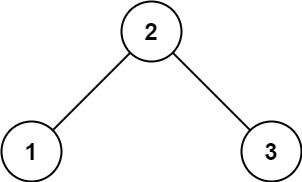
二叉搜索树
530. 二叉搜索树的最小绝对差(783题一样)
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。
输入:root = [4,2,6,1,3]
输出:1
输入:root = [1,0,48,null,null,12,49]
输出:1
解析过程:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
List<Integer> list=new ArrayList<>();
public int getMinimumDifference(TreeNode root) {
//先中序遍历,然后求差
if(root == null){
return 0;
}
InOrder(root);
int value=Integer.MAX_VALUE;
for(int i=1;i<list.size();i++){
value=Math.min(value,list.get(i)-list.get(i-1));
}
return value;
}
public void InOrder(TreeNode root){
if(root == null){
return;
}
InOrder(root.left);
list.add(root.val);
InOrder(root.right);
}
}
结果:
执行用时:1 ms, 在所有 Java 提交中击败了46.33%的用户
内存消耗:38.9 MB, 在所有 Java 提交中击败了14.61%的用户
通过测试用例:188 / 188
700. 二叉搜索树中的搜索
给定二叉搜索树(BST)的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 NULL。
例如,
给定二叉搜索树:
4
/ \
2 7
/ \
1 3
和值: 2
你应该返回如下子树:
2
/ \
1 3
在上述示例中,如果要找的值是 5,但因为没有节点值为 5,我们应该返回 NULL。
解析过程:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
//递归 二分
if(root == null){
return null;
}
if(root.val == val){
return root;
}else if(root.val > val){
return searchBST(root.left,val);
}else {
return searchBST(root.right,val);
}
}
}
结果:
执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
内存消耗:38.9 MB, 在所有 Java 提交中击败了95.56%的用户
通过测试用例:36 / 36
701. 二叉搜索树中的插入操作
给定二叉搜索树(BST)的根节点和要插入树中的值,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
示例 1:
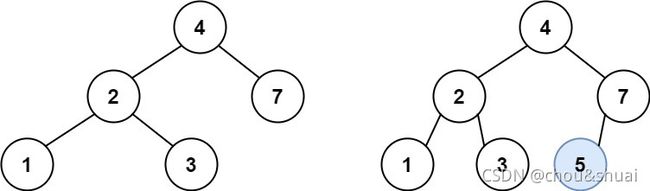
输入:root = [4,2,7,1,3], val = 5
输出:[4,2,7,1,3,5]
示例 2:
输入:root = [40,20,60,10,30,50,70], val = 25
输出:[40,20,60,10,30,50,70,null,null,25]
示例 3:
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出:[4,2,7,1,3,5]
解析过程:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
//可以先通过二分查找的方式找到需要插入的位置
if(root == null){
return new TreeNode(val);
}
TreeNode node=root;
while(node != null){
//如果节点值小于新值,在右子树上查找
if(node.val < val){
if(node.right == null){
node.right= new TreeNode(val);
break;
}else{
node = node.right;
}
}else {
if(node.left == null){
node.left=new TreeNode(val);
break;
}else {
node=node.left;
}
}
}
return root;
}
}
结果:
执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
内存消耗:39 MB,在所有 Java 提交中击败了65.23%的用户
通过测试用例:35 / 35
98. 验证二叉搜索树
(与面试题04.05.合法二叉树一样)
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
输入:root = [2,1,3]
输出:true
示例 2:

输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
解析过程:
方法一:
递归
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isValidBST(TreeNode root) {
//时间复杂度和空间复杂度都为O(n)
return isValidT(root,Long.MIN_VALUE,Long.MAX_VALUE);
}
public boolean isValidT(TreeNode root,long low,long high){
//递归DFS
//左子树的节点需要保证小于根节点,右子树的节点需要保证大于根节点
if(root == null){
return true;
}
//采用上界和下界到的思想
if(root.val<=low ||root.val>=high){
return false;
}
return isValidT(root.left,low,root.val) &