import math
import operator
def createDataSet():
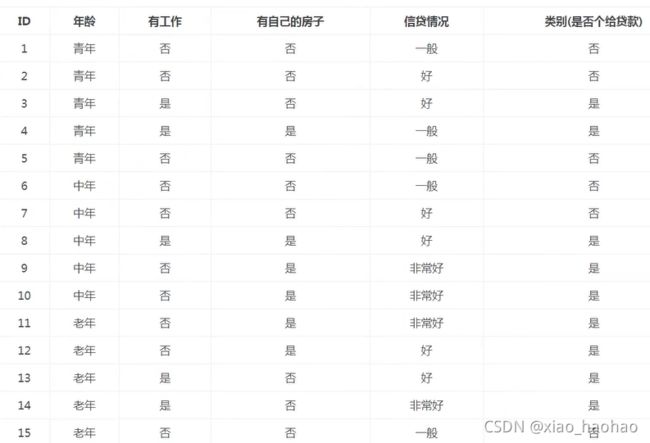
labels = ['年龄','工作','房子','信贷情况'] #特征标签
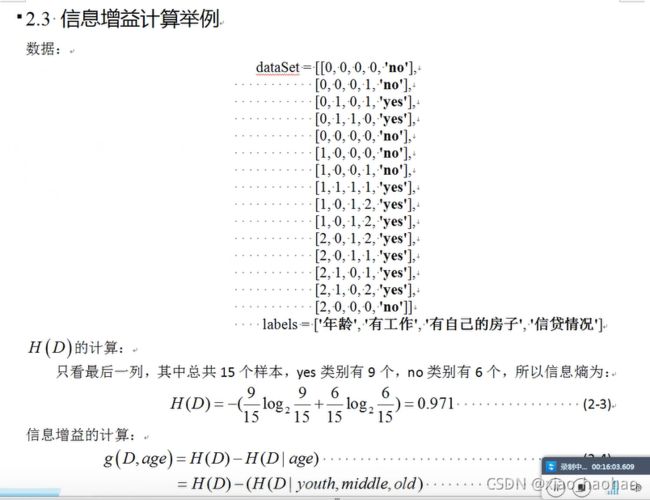
dataSet = [[0, 0, 0, 0, 'no'],
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']] #数据集
"""假设对于年龄而言,0代表youth,1代表middle,2代表old"""
return dataSet,labels
"""
splitDataSet(dataSet,axis,value)函数的功能:
例如 axis=0表示第一列属性年龄,value=1表示年龄属性的值为1的数据
那么返回的新数据集为
[[0, 0, 0, 'no']
[0, 0, 1, 'no']
[1, 1, 1, 'yes']
[0, 1, 2, 'yes']
[0, 1, 2, 'yes']]
即选出年龄属性值为1的向量,并把每个向量中年龄属性的分量值去掉
"""
def splitDataSet(dataSet,axis,value):
retDataSet = [] #创建返回的数据集列表
for featVec in dataSet: #遍历数据集,dataSet看作是矩阵(二维列表),featVec看作是向量(一维列表)
if featVec[axis] == value:
reducedFeatVec = featVec[:axis] #此行加下一行的代码表示把axis属性的值去掉,然后保存在reducedFeatVec中,是一个向量
reducedFeatVec.extend(featVec[axis+1:]) #列表.exteng(列表)表示给一个列表后面再追加一个列表,即合并两个列表 将符合条件的添加到返回的数据集
retDataSet.append(reducedFeatVec) #将上两行得到的向量追加到retDataSet矩阵中
return retDataSet #返回删减后的数据集,形如函数名上方注释给出的返回的新数据集的形式
#选择最优属性
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 #特征数量,-1是因为第五列是标签不是特征属性
baseEntrtopy = calcShannonEnt(dataSet) #计算总的数据集的信息熵
bestInfoGain = 0.0 #信息增益
bestFeature = -1 #最优特征的索引值(属性的列表下标)
for i in range(numFeatures): #遍历所有特征(一列一列来算)
featList = [example[i] for example in dataSet] #每一轮循环取出一个属性的所有值汇集到featList列表中 形如dataSet矩阵中的第一列[0,0,0,0,0,1,1,1,1,1,2,2,2,2,2]
"""
featList = []
for example in dataSet:
featList.append(example[i])
#此段代码等价于上面的一行代码
"""
uniqueVals = set(featList) #创建set集合,目的是使得元素不重复 形如对于dataSet矩阵中的第一列而言是{0,1,2}
newEntropy = 0.0 #总数据集在某一属性条件下的条件熵
for value in uniqueVals: #计算条件熵
subDataSet = splitDataSet(dataSet,i,value) #subDataSet划分后的子集
prob = len(subDataSet) / float(len(dataSet)) #计算西瓜书p75式(4.2)中的|Dv|/|D|
newEntropy = newEntropy + prob * calcShannonEnt(subDataSet) #计算条件熵
infoGain = baseEntrtopy - newEntropy #计算信息增益
#print("第%d个属性的信息增益为%.3f" % (i,infoGain)) #打印每个属性的信息增益
if (infoGain > bestInfoGain): #找出信息增益最大的属性
bestInfoGain = infoGain #更新
bestFeature = i #记录信息增益最大的属性的列表下标
return bestFeature #返回信息增益最大的属性的列表下标
def calcShannonEnt(dataSet): #计算数据集的信息熵,即西瓜书中的Ent(D),将子集传过来也可算子集的信息熵,即Ent(Dv)
numEntires = len(dataSet) #数据集的行数,即数据的总个数
labelCounts = {} #保存每种标签(yes,no)的出现次数的字典
for featVec in dataSet: #对每组特征向量(每一行)进行统计
currentLabel = featVec[-1] #提取标签信息,-1表示每个向量中的最后一个分量,即每个样本的标签
if currentLabel not in labelCounts.keys(): #如果标签没有放入统计次数的字典里,添加进去
labelCounts[currentLabel] = 0 #字典.[key]=value,给字典中的健赋值,此处的值表示标签出现的次数,初始化为0次
labelCounts[currentLabel] += 1 #给标签计数
shannonEnt = 0.0 #信息熵
for key in labelCounts: #计算信息熵
prob = float(labelCounts[key])/numEntires #该标签的概率,即西瓜书上的pk
shannonEnt = shannonEnt - prob * math.log(prob,2) #信息熵公式,此时求的是西瓜书p75最下面的那个式子
return shannonEnt #返回数据(子)集的信息熵
def majorityCnt(classList):
classCount = {}
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.items(),key = operator.itemgetter(1),reverse = True) #根据字典的值降序排序
return sortedClassCount[0][0]
#核心代码
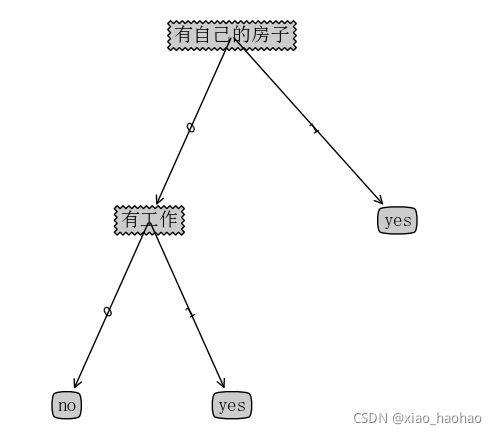
def createTree(dataSet,labels,featLabels):
classList = [example[-1] for example in dataSet] #取分类标签
if classList.count(classList[0]) == len(classList): #如果当前子集类别完全相同则停止继续划分(即只需要部分属性就可以完全正确划分)--第一个停止条件 count(value)函数描述:统计列表中value元素出现的次数
#此情况举例说明:假设通过年龄,工作,房子分类后的子集只有3个向量,且这三个向量的标签都是yes,那么就不需要再用信贷情况继续划分了,因为不管信贷情况如何,最终结果都是yes
return classList[0]
if len(dataSet[0]) == 1: #遍历完所有属性特征时返回出现次数最多的类标签(即全部属性用完也无法完全正确划分,到底给不给贷款通过投票决定)--第二个停止条件
#此情况举例说明:假设通过年龄,工作,房子,信贷情况分类后的子集有3个向量,且其中两个向量的标签是yes,一个向量标签是no,但是我们没有其他属性可以继续划分了,那么就投票决定是yes还是no,此处投票结果应是yes
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet) #选择最优特征
bestFeatLabel = labels[bestFeat] #最优特征的标签
featLabels.append(bestFeatLabel)
myTree = {bestFeatLabel:{}} #根据最优属性的标签生成树,数据类型是字典,最后输出时是{bestFeatLabel:{bestFeatLabel:{...},bestFeatLabel:{...},...}}这样的形式,每递归调用一次就会多嵌套一层bestFeatLabel:{},bestFeatLabel表示当前结点,{}表示他的分支
del (labels[bestFeat]) #删除已经使用的属性标签
featValues = [example[bestFeat] for example in dataSet] #得到训练集中所有最优属性的值
uniqueVals = set(featValues) #去掉重复的属性值,集合中元素的个数就是此节点将拥有的分支数
for value in uniqueVals: #递归创建决策树,每一轮循环创建一个分支
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),labels,featLabels) #取出当前集合最优属性值为value的向量并把每个向量的最优属性对应的分量去除,得到的子集用作下一轮递归的数据集
#https://www.jb51.net/article/157018.htm 字典[][]是字典里嵌套字典的用法,此处bestFeatLabel表示属性结点,value表示该属性结点分支的权值,例如{'工作': {0: 'no', 1: 'yes'}},myTree['工作'][0]的值为'no'
return myTree
#对测试样本进行分类
def classify(inputTree,featLabels,testVec):
firstStr = next(iter(inputTree)) #获取决策树结点
secondDict = inputTree[firstStr] #下一个字典,用来获取当前结点的分支上的权值
featIndex = featLabels.index(firstStr) #列表.index[列表值]表示列表中此列表值的下标 获取决策树当前结点(最优属性)在featLabels中的下标
for key in secondDict.keys(): #对决策树的查找
if testVec[featIndex] == key:
if type(secondDict[key]).__name__ == 'dict': #如果是字典,说明还没到叶子结点,那么要继续递归分类
classLabel = classify(secondDict[key], featLabels, testVec)
else: #如果不是字典,比如是字符串,那么说明已经是叶子结点了,查找完成,不用再递归下去了
classLabel = secondDict[key]
return classLabel #返回叶子结点的值
if __name__ == '__main__' :
dataSet , labels = createDataSet()
#print("最优特征属性:" + str(chooseBestFeatureToSplit(dataSet))) #测试使用
featLabels = [] #按次序把最优属性保存到此列表中,此列表对于创建决策树无用,但是后面测试样本的classify(myTree,featLabels,testVec)函数需要使用
myTree = createTree(dataSet,labels,featLabels)
print(myTree)
testVec = [0,1,0,1] #测试数据
result = classify(myTree,featLabels,testVec)
if result == 'yes':
print("放贷")
if result == 'no':
print("不放贷")


