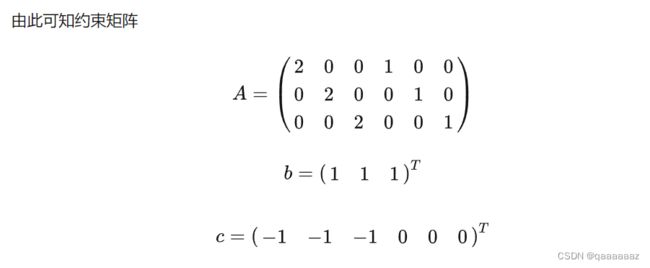线性规划问题
一、什么是线性规划
线性规划是最优化问题的一种特殊情形,实质是从多个变量中选取一组合适的变量作为解,使得这组变量满足一组确定的线性式(约束条件),而且使一个线性函数(目标函数)达到最优。线性规划顾名思义,由两个关键的部分组成:线性和规划。
线性
如果一个函数L(x)满足可加性和齐次性两个条件,则表明该函数是线性的。
(1)可加性:L(x+y)=L(x)+L(y)
(2)齐次性:αL(x)=L(αx)
我们也经常把一阶多项式函数 L(x)=kx+b 称之为线性的,其中 是常数。不难验证一阶多项式函数也满足上述可加性和齐次性的条件。
规划
谈到规划这个名词我们就不得不回归到线性规划的英文去谈(Linear Programming)。Programming 在英文中本意是编程的意思。实际上用 Linear Programming 来命名优化问题在今天来看稍显奇怪,Programming 是计算机编程的意思,貌似和我们今天谈的主题关系不大。这里边还有一个大背景就是 1946年 世界上第一台电子计算机在美国宾夕法尼亚大学诞生,也就是说在那个时间节点来看 计算机是非常非常时髦的一个东西,计算机编程也代表着最前进最前沿的新技术。那么自然以 Programming 来命名自己所研究的问题 就显得非常的高大上。
二、线性规划数学模型
满足以下三个条件的数学模型称为线性规划:
1、该问题可以用一组变量(决策变量)来表示一个解决方案。
2、有目标函数,是决策变量的线性函数。
3、有约束条件,可用一组线性等式或者不等式来表示。
线性规划问题的一般形式为:

式中,c1,c2,…cn叫做目标函数系数或者价值系数,b1,b2,…,bn叫做资源系数。
三、线性规划问题的标准形式
线性规划问题的标准形式是目标函数要求最小,所有约束条件都是等式约束,且所有的决策变量都是非负的。

其化简形式为:

用矩阵形式表示:
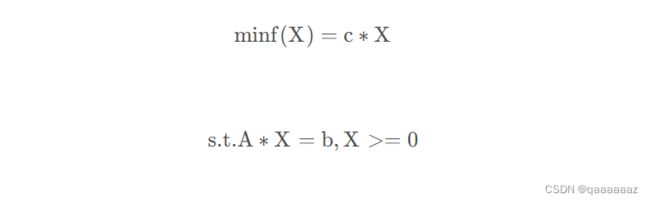
任意的线性规划问题都可以转化为标准形式:
1,若目标函数求求最大值,则只需要将目标函数的系数乘-1,就可以变为求解最小值问题,求得其最优解后,把最优目标函数值反号即得原问题得目标函数值。
2,若约束条件为不等式,若是“<=“则加入松弛变量,若是”>=”,则加入剩余变量,将不等式变为等式。
3,对于无约束得变量Xk,可令Xk=X1-X2,(X1;X2>=0)
四、线性规划问题的求解
4.1 线性规划图解法
4.1.1 图解法
考虑如下的线性规划问题:

使用画图的方式求解这个线性规划:
我们首先根据根据约束条件(1.2-1.5)画出可行域(图中蓝色部分),然后画出目标函数等高线(图中红色虚线)。紧接着我们想办法让红色虚线和可行域相切,相切的那个点就是最优解(对应图中情况A)。在寻找相切点的过程中,我们可能会经历几种情况:
情况B就是可行域在目标函数等高线的下方;
情况C就是将可行域分为两部分;
情况D是可行域在目标函数上方。
情况BCD都不是我们想要的结果,只有情况A是最优解。
以上就是线性规划画图求解的直观过程。
4.1.2 图解优势
图解法简单、直观,便于初期对线性规划问题的原理和几何意义进行深入理解。
4.1.3 图解法局限性
适用于两个或者三个变量,如果是两个变量,需要绘制直角坐标系;如果是三个变量,需要绘制立体坐标系。所以实际情况下,我们一般使用单纯型法求线性规划的解。单纯型法适用于任意变量,但是必须将线性规划数学模型转换为标准形式。
4.2 穷举顶点法
4.2.1 线性规划基本定理
对于标准形式的线性规划问题,如果该问题存在有界的最优解,那么至少有一个最优解在顶点上。
4.2.2 穷举顶点法
根据线性规划基本定理,我们不难想到一个求解线性规划最优解的方法:穷举所有顶点,然后找出目标函数最优的那个顶点。
那么对于一般的标准形式的线性规划问题的穷举顶点算法为:
Step 1: 从 个变量中任意抽取其中m个,然后将剩余的n-m个变量赋值为0。
Step 2: 抽取得到的m个变量构成m乘m的方程组,求解这个方程组即可获得顶点。
Step 3: 判断这个顶点是否满足约束x>=0,若不满足则舍弃掉,若满足则保存该顶点。
4.2.3 穷举顶点法局限
从上述算法流程中不难看出,计算量非常大,那么有没有更加效率的方法求解线性规划问题呢?于是就引出了单纯型法。
4.3 单纯型法
4.3.1单纯型算法大致框架
Step 1:从一个初始的基可行解出发;
Step 2:检查是否是最优解(最优解条件),若是最优解则停止,否则进入下一步;
Step 3:从当前基可行解移动到更好的基可行解,然后跳转到 Step 2;
上述算法即为单纯型算法的最基本的步骤。
对比穷举算法和单纯形算法可以发现: 在第1节中的穷举算法中,我们是把所以的顶点都拿出来比较一番,然后就可以找出最优解了。单纯型法和穷举算法的主要区别在于 单纯型法是一个迭代的方法。单纯型法是通过从一个可能不是很优的可行解出发,然后逐步逐步改进这个可行解,直至达到最优解。
显然,在上述算法过程中我们需要解决三个主要的问题:
1、如何找到一个初始的基可行解;
2、如何检查当前解是否是最优解;
3、如何从当前的基可行解移动到更好的基可行解;
如何找到一个初始的基可行解
判断是否得到最优解
如何从当前的基可行解移动到更好的基可行解
一般情况,顶点 v i vi vi和顶点 v j vj vj 是相邻节点的定义为 v i vi vi和 v j vj vj的非基变量只有一个不一样,基变量也只有一个不一样,其余变量均相等.进一步将这一过程用代数方式严谨表示出来,其中 B ∈ R m ∗ m , N ∈ R m ∗ ( n − m ) B∈R^{m*m},N∈R^{m*(n-m)} B∈Rm∗m,N∈Rm∗(n−m)
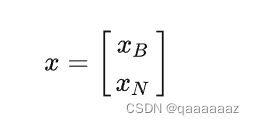
其中 x B ∈ R m x_B∈R^m xB∈Rm是基变量, x N ∈ R ( n − m ) x_N∈R^{(n-m)} xN∈R(n−m)。
由此将线性规划改写为如下形式:
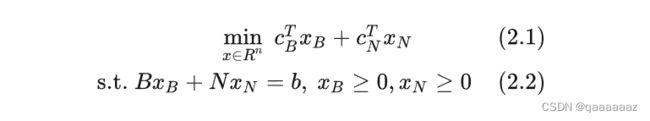
于是

在非基变量中我们选择其中一个分量 x q x_q xq进入到 基变量中

A q A_q Aq是与 x q x_q xq所对应的 A A A的列。式(2.4)反映了基变量和非基变量之前的关系。
设当前的解为x,我们想要得到下一步的解为 x ( λ ) x(\lambda) x(λ)

其中 d q d_q dq为搜索方向, λ > 0 \lambda>0 λ>0为搜索步长。 d q ∈ R n , e q ∈ R ( n − m ) d_q∈R^n,e_q∈R^{(n-m)} dq∈Rn,eq∈R(n−m)其在 x q x_q xq对应的位置为1,其余位置为0.
4.3.2 单纯型算法流程
Step 1: 找到基可行解 x x x , 设其基矩阵为 B B B 和非基矩阵 N N N ;
Step 2: 根据式(2.8)计算所有非基矩阵的 r q r_q rq ,若所有的 r q > = 0 r_q>=0 rq>=0则停止输出最优解;否则 跳转到 Step 3;
Step 3: 根据式(2.5)计算移动方向 d q d_q dq ,若 d q > = 0 d_q>=0 dq>=0, 则表明线性规划是无界的。 否则,根据式(2.10)计算出步长 λ \lambda λ 。更新 x ← x + λ d q x\leftarrow x+\lambda d_q x←x+λdq,然后更新基矩阵,并跳转到 Step 2;
4.3.3单纯型算法计算流程实例
实例一
实例二
【运筹学】线性规划数学模型 ( 单纯形法 | 最优解判定原则 | 线性规划求解示例 )by韩曙亮
参考
[1]一、线性规划byZJH01080108
[2]运筹学与控制论by王源