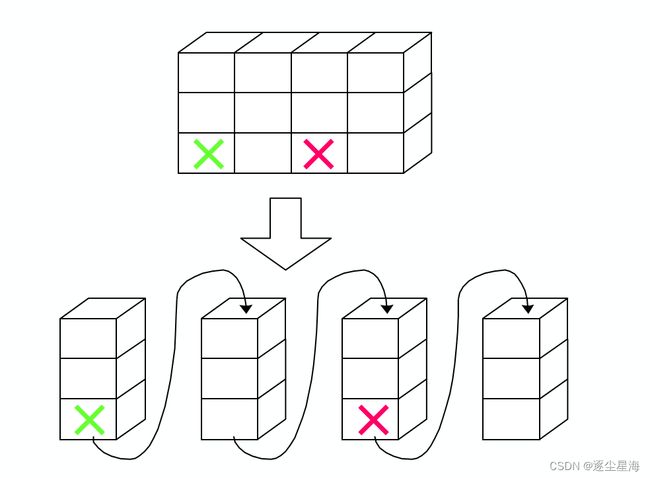
数据结构：串、数组和广义表

串

 

线性结构：线性表、栈和队列、串与数组和广义表

串的逻辑结构和线性表极为相似，区别仅在于串的数据对象限定为字符集。在基本操作上,串和线性表有很大差别。线性表的基本操作主要以单个元素作为操作对象，如查找、插入或删除某个元素等;而串的基本操作通常以子串（串的整体）作为操作对象，如查找、插入或删除一个子串等。

一、串的类型定义

串(String)----零个或多个字符组成的有限序列,数据元素是一个字符

【定义】由零个或多个字符组成的有限序列， 一般记为 s= "a1 a2 … an" (n≥O)

【串名】s就是串的名字。

【串值】由双引号括起来的字符序列就是串的值

【串长】串中字符的数目n即为串长

【空串】零个字符的串，其长度为零。注意空格串与空串的区别。

【子串】串中任意个连续的字符组成的子序列称为该串的子串。

• 子串个数：((n+1)*n/2)+1——+1为空串

• e.g. software 的子串数量为 ((8+1)*8/2)+1 = 37

【主串】包含子串的串相应地称为主串。

【空格串】 由一个或多个空格组成的字符串。

抽象数据类型

ADT String {
数据对象: D={ ai | ai∈ CharacterSet,记为 V,i=1 ,2 ,…, n,n≥ 0 }
结构关系: R={< ai,ai + 1 >| ai,ai + 1 ∈ V,i=1 ,…, n-1 ; n-1 ≥ 0 }
基本操作:

( 1 ) StrAssign( &S,chars)
操作前提: chars 是字符串常量。
操作结果:生成一个值等于 chars 的串 S。

( 2 ) StrInsert( S,pos,T)
操作前提:串 S 存在,1 ≤ pos≤ StrLength( S)+ 1 。
操作结果:在串 S 的第 pos 个字符之前插入串 T。

( 3 ) StrDelete( &S,pos,len)
操作前提:串 S 存在,1 ≤ pos≤ StrLength( S)+ 1 。
操作结果:从串 S 中删除第 pos 个字符起长度为 len 的子串。

( 4 ) StrCopy( S,&T)
操作前提:串 S 存在。
操作结果:由串 S复制得串 T。

( 5 ) StrEmpty( S)
操作前提:串 S 存在。
操作结果:若串 S 为空串,则返回 TRUE,否则返回 FALSE。

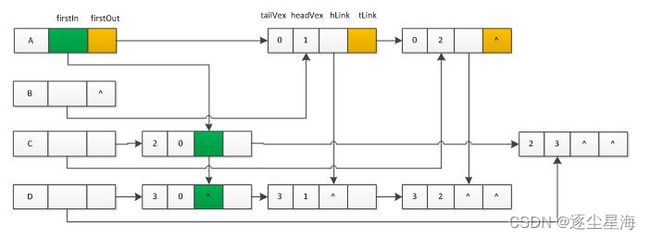
( 6 ) StrCompare( S,T)
操作前提:串 S 和 T 存在。
操作结果:若 S>T,则返回值>0 ;如 S=T,则返回值=0 ;若 S

( 7 ) StrLength( S)
操作前提:串 S 存在。
操作结果:返回串 S 的长度,即串 S 中的字符个数。

( 8 ) StrClear( &S)
操作前提:串 S 存在。
操作结果:将 S 清为空串。

( 9 ) StrCat( S,T)
操作前提:串 S 和 T 存在。
操作结果:将串 T 的值连接在串 S 的后面。

( 10 ) SubString( &Sub,S,pos,len)
操作前提:串 S 存在,1 ≤ pos≤ StrLength( S)且 1 ≤ len≤ StrLength( S)- pos+1
操作结果:用 Sub 返回串 S 的第 pos 个字符起长度为 len 的子串。

( 11 ) StrIndex( S,pos,T)
操作前提:串 S 和 T 存在,T 是非空串,1 ≤ pos≤ StrLength( S)。
操作结果:若串 S 中存在和串 T 相同的子串,则返回它在串 S 中第 pos 个字符 之后第一次出现的位置;否则返回 0 。

( 12 ) StrReplace( &S,T,V)
操作前提:串 S、 T 和 V 存在且 T 是非空串。
操作结果:用 V 替换串 S 中出现的所有与 T 相等的不重叠的子串。

( 13 ) StrDestroy( S)
操作前提:串 S 存在。
操作结果:销毁串 S。

}ADT string

int Index(Sring S, String T){
    int i = 1, n = StrLength(S), m = StrLength(T);
    String sub;
    while(i <= n-m+1){
        SubString(&sub, S, i, m);   //取主串第i个位置，长度为m的串给sub
        if(StrCompare(sub, T) != 0){
            ++i;
        }else{
            return i;   //返回子串在主串中的位置
        }
    }
    return 0;   //S中不存在与T相等的子串
}

二、存储结构

串也有顺序存储和链式存储两种存储方式，但大多采用顺序存储。

1.串的顺序存储

1）串的定长顺序存储结构：

为每个定义的串变量分配一个固定长度的存储区域。

特点: 静态的，编译时就确定了串的空间大小。

#define MAXLEN 255
typedef struct{
   char ch[MAXLEN+1];      //若串非空,则按串长分配存储区,否则ch为NULL
   int  length;   //串长度
}SString;

2）串的堆式顺序存储结构：

在C语言中，存在一一个称之为“堆”的自由存储区，并用malloc()和free()函数来完成动则返回一个指向起始地址的指针，作为串的基地址，这个串由ch指针来指示;若分配失败，则返回NULL。已分配的空间可用free()释放掉。

typedef struct{
    char *ch;   //按串长分配存储区，ch指向串的基地址
    int length; //串的长度
}HString;

2.串的链式存储

#define CHUNKSIZE 80       //可由用户定义的块大小
typedef struct Chunk{
   char  ch[CHUNKSIZE];
   struct Chunk *next;
}Chunk;
​
typedef struct{
   Chunk *head,*tail;      //串的头指针和尾指针
   int curlen;             //串的当前长度
}LString;

链式存储的操作方便，但是存储密度小。结点大小的选择直接影响着串处理的效率。

三、串的模式匹配

子串的定位运算通常称为串的模式匹配或串匹配。

算法目的：确定主串中所含子串第一次出现的位置（定位）

1.BF算法

子串的定位操作通常称为串的模式匹配，它求的是子串(常称模式串)在主串中的位置。这里采用定长顺序存储结构，给出一种不依赖于其他串操作的暴力匹配算法。

古典的，经典的，朴素的，穷举的

算法原理：

• 将主串的第pos个字符和模式的第一个字符比较，

  • 若相等，继续逐个比较后续字符；

  • 若不等，从主串的下一字符起，重新与模式的第一个字符比较。

• 直到主串的一个连续子串字符序列与模式相等 。返回值为S中与T匹配的子序列第一个字符的序号，即匹配成功。

• 否则匹配失败，返回值为 0

匹配示意图：

 

伪代码:

int Index_BF(SString S, SString T, int pos)
{
    i=pos; j=1;
    while(i<=S.length && j<=T.length){
        if(S.ch[i]==T.ch[j]){
            i++; j++
        }else{
            i=i-j+2; j=1;
        }
    }
    if(j>T.length) return i-T.length;  // 匹配成功
    else return 0  // 匹配失败
}

算法分析

简简单的模式匹配算法的最坏时间复杂度为O(nm)，主串长度为n，子串长度为m。

• 总次数为：(n-m)*m+m＝(n-m+1)*m若m<，则算法复杂度O(n*m)

• 最好情况下的时间复杂度为O(n+m)

• 最坏情况下的时间复杂度为O(nm)

• 因为在匹配失败后，主串的指针总要回溯到i-j+2的位置，所以时间复杂度高

2.KMP算法

kmp算法可以看作是对BF算法的改进

（配合下方这两个up的两个链接进行理解）

介绍：

改进：每趟匹配过程中出现字符比较不等时，不回溯主指针i，利用已得到的“部分匹配”结果将模式向右滑动尽可能远的一段距离，继续进行比较。

从分析模式本身的结构着手，如果已匹配相等的前缀序列中有某个后缀正好是模式的前缀，那么就可以将模式向后滑动到与这些相等字符对齐的位置，主串i指针无须回溯，并继续从该位置开始进行比较。而模式向后滑动位数的计算仅与模式本身的结构有关，与主串无关！！！

KMP算法的特点：仅仅后移模式串，比较指针不回溯。

（对处理从外设输入的庞大文件很有效，可以边读入边比较）

算法原理：

kmp算法的讲解可以看天道酬勤的视频：【「天勤公开课」KMP算法易懂版】「天勤公开课」KMP算法易懂版_哔哩哔哩_bilibili

算法步骤：

• 求出模式串的next函数值

  • next[ j ]的含义是: 在子串的第j个字符与主串发生失配时,则跳到子串的next[ j ]位置重新与主串当前位置进行比较。

  • next[j]=最大公共前后缀长度+1

• 对模式串与主串进行匹配比较。

  • 若匹配则：比较下一个位置

  • 若不匹配则：模式串的下标通过next函数的数值进行移动

代码：

代码讲解：【KMP算法之求next数组代码讲解】KMP算法之求next数组代码讲解_哔哩哔哩_bilibili（这个up讲的真的很清楚，一定要看！）

int Index_KMP (SString S,SString T, int pos) 
{      
       i= pos,j =1;
       while (iT.length)  return i-T.length;  /*匹配成功*/
       else   return 0;              /*返回不匹配标志*/
} 
​
// 求next数组 
void get_next(String T, int *next){
    int i = 1, j = 0;
    next[1] = 0;
    while (i < T.length){
        if(j==0 || T.ch[i]==T.ch[j]){   //ch[i]表示后缀的单个字符，ch[j]表示前缀的单个字符
            ++i; ++j;
            next[i] = j;    //若pi = pj， 则next[j+1] = next[j] + 1
        }else{
            j = next[j];    //否则令j = next[j]，j值回溯，循环继续
        }
    }
}

next数组求解：

• next[j+1]的最大值为next[j]+1。

• 如果Pk1不等于Pj，那么next[j+1]可能的次大值为next[next[j]]+1，以此类推即可高效求出next[j+1]。(重点)

KMP算法改进

如果出现了上述的情况则需要再次递归，将next[j]修正为next[next[j]],直至两者不相等为止，更新后的数组命名为nextval。计算next数组修正值的算法如下，此时匹配算法不变。

void get_nextval(String T, int *nextval){
    int i = 1, j = 0;
    nextval[1] = 0;
    while (i < T.length){
        if(j==0 || T.ch[i]==T.ch[j]){   //ch[i]表示后缀的单个字符，ch[j]表示前缀的单个字符
            ++i; ++j;
​
            if(T.ch[i] != T.ch[j]){ //若当前字符与前缀字符不同
                nextval[i] = j; //则当前的j为nextval在i位置的值
            }else{
                //如果与前缀字符相同
                //则将前缀字符的nextval值给nextval在i位置上的值
                nextval[i] = nextval[j];
            }
        }else{
            j = nextval[j]; //否则令j = next[j]，j值回溯，循环继续
        }
    }
}

例题 【单选题】Nextval在next的基础上得到的,已知串T “abab”的next数组为0112, J: 1 2 3 4 T串: a b a b next[j]: 0 1 1 2 nextval[j]: 0 1 0 1 求解过程如下: 首先nextval[1]=0, 因为next[2]=1,所以比较串T[2](即b)与T[1]( 即a),因为不相等,所以nextval[2]=next[2]=1; 因为next[3]=1,所以比较串T[3]( 即a)与T[1]( 即a),因为相等,所以nextval[3]=nextval[1]=0; 因为next[4]=2,所以比较串T[4]( 即b)与T[2]( 即b),因为相等,所以nextval[4]=nextval[2]=1 据此求得串“ababaabab”的nextval为()。 A. 010104101 B. 010102101 C. 010100011 D. 010101011

答案选A

注:本题在题目中详细的讲解了nextval数组的求法，可以作为理解的参考。

参考资料：

1. 严蔚敏、吴伟民：《数据结构（C语言版）》

2. 数据结构：串(String)【详解】UniqueUnit的博客-CSDN博客串数据结构

数组

一、数组的类型定义

数组是由类型相同的数据元素构成的有序集合，每个元素称为数组元素，每个元素受n个线性关系的约束（每个元素都在n个关系中，所以，可以通过下标访问对应的元素。

数组可以看成是线性表的推广，其特点是结构中的元素本身可以是某种结构的数，但属于同一数据类型。从组成线性表的元素角度看，数组是由具有某种结构的数据元素构成，广义表则是由单个元素或子表构成的。

• 与其他线性结构关系：

  • 一维数组即为线性表，而二维数组可以定义为其数据元素为一维数组（线性表）的线性表。以此类推，N维数组是数据元素为N-1维数组的线性表。

  • 从本质上讲，数组与顺序表、链表、栈和队列一样，都用来存储具有 "一对一" 逻辑关系数据的线性存储结构。

• 存储结构：高级语言中的数组是顺序结构；数据结构中的数组既可以是顺序的，也可以是链式结构。

抽象数据类型

ADT Array { 数据对象： ji = 0, ... , bi-1, i = 1, 2, ... , n, D = {aj1j2...jn|n ( >0 ) 称为数组的维数， bi是数组第i维的长度，ji是数组元素的第i维下标，aj1j2...jn属于ElemSet }

aabcde…… a是数组a的一维下标，若a=4，那么数组a的第一维的长度为4 b是数组a的二维下标，若b=6，那么数组a的第二维的长度为6 e是数组a的五维下标，若e=5，那么数组a的第五维的长度为5

数据关系： R = { R1, R2, R3..., Rn} Ri = {|0<=jk<=bk-1 , 1<=k<=n 且 k不等于i , 0<=ji<=bi-2 , aj1...j1...jn与a~j1...j1+1...属于D,i=2,L,n}

a233是a234的直接前驱 a235是a234的直接后继

基本操作： （1）InitArray(&A,n,boundi,…,boundn) 操作结果：若维数n和各维长度合法，则构造相应的数组A,并返回OK （2）DestroyArray(&A) 操作结果：销毁数组A （3）Value(A,&e,index1,…,indexn) 初始条件：A是n维数组，e为元素变量，随后是n个下标值。 操作结果：若各下标不越界，则e赋值为所指定的A的元素值，并返回OK （4）Assign(&A,e,index1,…indexn) 初始条件：A是n维数组，e为元素变量，随后是n个下标值。 操作结果：若下标不越界，则e的值赋给所指定的A的元素，并返回OK

}ADT Array

注：数组元素个数的计算：a342 那么数组共有3维,长度分别为3,4,2，一共有3*4*2=24个元素

二维数组

二维数组可以看作是线性表的线性表：

 二维数组有行列之分，因此，有两种顺序存储方式

• 以行序为主序（低下标优先）BASIC、COBOL、PASCAL、C、JAVA、Basic

• 以列序为主序（高下标优先）FORTRAN

三维数组

二、数组的顺序存储

数组的基本操作不涉及数组结构的变化（插入、删除）。因此对于数组而言，采用顺序存储表示比较适合。

存储原理： 内存储器的结构是一维的，对于一维数组可直接采用顺序存储，用一维的内存存储表示多维数组，就必须按照某种次序将数组中元素排成一个线性序列，然后将这个线性序列存放在一维的内存储器中，这就是数组的顺序存储结构。

多维数组的存储

二维数组Amn：

• 以行为主的存储序列为：a11,a12,…,a1n,a21,a22,…,a2n,…,am1,am2,…,amn

• 以列为主的存储序列为：a11,a21,…,am1,a12,a22,…,am2,…,a1n,a2n,…,amn

   

数组地址计算

计算：若数组的下标从（0，0）开始 （1）一维数组的地址计算 Loc(A[i])=Loc(A[0])+i✖size

（2）二维数组的地址计算 如果每个元素占size个存储单元： Loc(A[i][j])=Loc(A[0][0])+(i✖n+j)✖size 如果每个元素占一个存储单元： Loc(A[i][j])=Loc(A[1][1])+(i-1)✖n+(j-1)

• 如LOC(0, 0)是a00的地址 LOC(2, 2) = LOC(0, 0) + (2*3+2)L (L为每个元素占的存储单元) 解释：LOC(0,0)为第一个元素的地址。 2 * 3中的2表示2个第一维数组，3表示数组第二维的长度，3 * 2可以理解为跳过长度2的第一维数组，直接到LOC(2,0). +2表示跳过长度为2的第二维数组,所以就到LOC(2,2)了

• 行序为主序：LOC(i, j) = LOC(s,t) + ((i-s)✖(n-t+1)+(j-t))✖L 解释：假设二维数组A[s...m , t...n],每个元素占L个存储单位，LOC(i,j) 是aij的存储位置，LOC(s,t) 是ast的存储位置，即数组的起始存储位置。当数组以行序为主序进行存储的时候，则元素aij的前面存储了 (i-s) 行元素，每行有 (n-t+1) 个元素，aij所在行的全面则存储了j-t个元素。

• 列序为主序：LOC(i, j) = LOC(s,t) + ((j-t)✖(m-s+1)+(i-s))✖L 解释：假设二维数组A[s...m , t...n],每个元素占L个存储单位，LOC(i,j) 是aij的存储位置，LOC(s,t) 是ast的存储位置，即数组的起始存储位置。当数组以行序为主序进行存储的时候，则元素aij的前面存储了 (j-t) 列元素，每列有 (m-s+1) 个元素，aij所在列的前面面则存储了s-i个元素。

（3）三维数组的地址计算 Loc(A[i][j][k])=Loc(A[0][0][0])+(i✖m✖n+j✖n+k)✖size 当 j1，j2，j3的下限分别为c1，c2，c3，上限分别为d1,d2,d3时 Loc(A[j1][j2][j3])=Loc(A[c1][c2][c3])+(j1-c1)✖((d2-c2+1)✖(d3-c3+1)+(j2-c2)✖(d3-c3+1)+(j3-c3))✖size

（4）n维数组的地址计算 Loc(A[j1][j2]…[jn])=Loc(A[c1][c2]…[cn])+Σ(i=1到n)ai✖(ji-ci) 其中，ai=size✖Π(k=i+1到n)(dk-ck+1),1≤i≤n

由于计算各个元素存储位置的时间相等，所以存取数组中任一元素的时间也是相等的，即数组是一种随机存取结构。

三、特殊矩阵的压缩存储

压缩存储：是指为多个值相同的元只分配一个存储空间，对零元不分配空间。

1.对称矩阵

数组中元素满足公式：aij==aji ,即数据元素沿主对角线对应相等，这类矩阵称为对称矩阵。

所以我们只存储上三角/下三角矩阵（对角线+对角线上/下部分的元素）

公式：

最终求得的 k 值即为该元素存储到数组中的位置（矩阵中元素的行标和列标都从 1 开始）。

若存储下三角矩阵，则存储元素aij全都有i>=j（1==j时，k=i(i-1)/2+j-1 当j>=i时，k=j(j-1)/2+i-1(即用aji对应了上三角的aij)

此时一维数组sa[k]=aij，有了对应关系。

代码实现

对称矩阵的存储

#include 
#define len 5
​
int main(){
    //定义对称矩阵
    int A[len][len] = {1,2,3,4,5,
                       2,3,4,5,6,
                       3,4,5,6,7,
                       4,5,6,7,8,
                       5,6,7,8,9};
​
    //定义存储数组
    int B[len*(len + 1) / 2];
​
    //进行压缩存储
    for(int i = 0;i < len ;i++){
        for(int j = 0;j <= i;j++){
            if (i >= j) {
                B[i*(i+1)/2+j] = A[i][j]; // 二维转一维
            } else break;
        }
    }
    printf("压缩矩阵的元素是：\n");
​
    //输出B中元素
    for (int k = 0; k < len*(len + 1) / 2; ++k) {
        printf("%d ",B[k]);
    }
    return 0;
} 

输出结果：

压缩矩阵的元素是：
1 2 3 3 4 5 4 5 6 7 5 6 7 8 9

对称矩阵的应用

#include 
#include 
#define M 10
#define N 4
int main()
{
    // 定义M和N两个对称矩阵
    int a[M]={1,2,3,4,5,6,7,8,9,10};
    int b[M]={1,1,1,1,1,1,1,1,1,1};
    int c[N][N],d[N][N];
    int i,j,k=0,s;
    // 将压缩存储的对称矩阵“解压”
    for(i=0;i

输出结果：

1、输出对称矩阵M：
1 2 4 7
2 3 5 8
4 5 6 9
7 8 9 10
2、输出对称矩阵N：
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
3、两个对称矩阵M、N的积为：
14 18 24 8
14 18 24 9
14 18 24 10
14 18 24 11

2.三角矩阵

对角线以下(或者以上)的数据元素(不包括对角线)全部为常数c。

存储方法：重复元素c共享一个元素存储空间，共占用n(n+1)/2+1个元素空间: sa[1.. n(n+1)/2+1]

 

存储原理：详情见可以在这个博客里看到，讲的非常详细：数据结构-二维数组-三角矩阵压缩存储majinshanNUN的博客-CSDN博客三角矩阵压缩存储公式

三角矩阵位置计算：Loc( aij)=Loc(a11)+[ i*(i-1)/2 +(j-1)]*L

代码实现（下三角）

#include
​
int main() {
    int a[5][5] = {
                    1, 0, 0, 0, 0,
                    5, 9, 0, 0, 0,
                    4, 6, 8, 0, 0,
                    2, 3,44,55, 0,
                    7,11,12,13,14，
                  };
    //这个转化公式很重要
    int len = sizeof(a[5])/sizeof(int);
    int b[len*(len+1)/2], x, y, k;
​
    printf("原二维数组：\n");    //输出原二维数组
​
    for (x = 0; x < len; x++){
        for (y = 0; y < len; y++){
            if (a[x][y] < 10){ // 使得输出更加整齐
                printf("%d  ", a[x][y]);
            } else {
                printf("%d ", a[x][y]);
            }
        }
        printf("\n");
    }
​
    printf("压缩后的一维数组:\n");
    
// 这里是压缩的重点！！！
    for (int i = 0; i < len; i++){         //将二维数组中非0值压缩至一维数组中
        for (int j = 0; j < len; j++){
            if (i >= j) {   //特殊矩阵，只压下三角的值
                k = i * (i + 1) / 2 + j;  // 二维数组和一维数组中原值的对应关系
                b[k] = a[i][j];
            } else break; // 提升性能
        }
    }
​
    for (int l = 0; l < len*(len+1)/2; l++){      //输出一维数组
        printf("%d ", b[l]);
    }
​
    printf("\n");
    printf("输入要查询的 行号&&列号 : ");   //输出要查询的数据
    scanf("%d%d", &x, &y);
    printf("\n");
    printf("您查询的数据是: ");
    
// 这里在压缩后的数组里查找数值：
    if (x < y)  printf("0\n");  //如果上三角直接输出0
    else printf("%d\n", b[(x - 1) * (x) / 2 + y - 1]);  // 下三角输出一维数组中对应的值
​
    return 0;
}

输出结果：

原二维数组：
1  0  0  0  0
5  9  0  0  0
4  6  8  0  0
2  3  44 55 0
7  11 12 13 14
压缩后的一维数组:
1 5 9 4 6 8 2 3 44 55 7 11 12 13 14
输入要查询的 行号&&列号 : 3 2
​
您查询的数据是: 6

3.对角矩阵

若一个n阶方阵A满足其所有非零元素都集中在以主对角为中心的带状区域中，则称其为n阶对角矩阵。非零元素集中在主对角线及其两侧共L(奇数)条对角线的带状区域内 — L对角矩阵。

三对角矩阵：

 

对角矩阵的位置计算：Loc(aij)=Loc(a11)+2(i-1)+(j-1)

对角矩阵

 

 4.稀疏矩阵

三元组法(顺序存储)

顺序存储的方法：又称有序的双下标法，只存储矩阵中的非 0 元素，与前面的存储方法不同，稀疏矩阵非 0 元素的存储需同时存储该元素所在矩阵中的行标和列标。（三元组储存）

注意：为更可靠描述，通常再加一个“总体”信息:即总行数、总列数、非零元素总个数。

特点：

• 优点：非零元在表中按行序有序存储，便于进行按行顺序处理的矩阵运算。

• 缺点：不能随机存取，若按行号存取某一行中的非零元，则需从头开始进行查找。

行逻辑链接顺序表(顺序存储)

三元组顺序表每次提取指定元素都需要遍历整个数组，运行效率很低。 行逻辑链接的顺序表。它可以看作是三元组顺序表的升级版，即在三元组顺序表的基础上改善了提取数据的效率。

步骤：

• 将矩阵中的非 0 元素采用三元组的形式存储到一维数组 data 中，如图 2 所示（和三元组顺序表一样）

• 使用另一个数组记录矩阵中每行第一个非 0 元素在一维数组中的存储位置。

优点：如果想从行逻辑链接的顺序表中提取元素，则可以借助 第二个 数组提高遍历数组的效率。

十字链表法(链式存储)

十字链表法存储稀疏矩阵，该存储方式采用的是 "链表+数组" 结构

参考资料：数据结构（七）数组和广义表 - 简书 (jianshu.com)

优点：它能够灵活地插入因运算而产生的新的非零元素，删除因运算而产生的新的零元素，实现矩阵的运算。

在十字链表中，矩阵的每一个非零元素用一个结点表示，该结点除了（row，col，value）外，还有两个域：

right： 用于链接同一行中的下一个非零元素；

down：用以链接同一列中的下一个非零元素。

使用十字链表压缩存储稀疏矩阵时，矩阵中的各行各列都各用一个链表存储，与此同时，所有行链表的表头存储到一个数组（rhead），所有列链表的表头存储到另一个数组

拿结点A说明，该结点对应两个链表（绿色和黄色标记的）。绿色链表表示以结点Ａ为弧头的弧组成的链表。黄色链表表示以结点Ａ为弧尾的弧组成的链表。如下图所示：

 

5.矩阵运算

该板块的所有内容均来自下面的博客：

作者：hadoop_a9bb 链接：https://www.jianshu.com/p/d7d5545012e2 来源：简书

稀疏矩阵的快速转置算法

稀疏矩阵快速转置算法和普通算法的区别仅在于第 3 步，快速转置能够做到遍历一次三元组表即可完成第 3 步的工作。 稀疏矩阵的快速转置是这样的，在普通算法的基础上增设两个数组（假 设分别为 array 和 copt）：

• array 数组负责记录原矩阵每一列非 0 元素的个数。以图 1 为例，则对应的 array 数组如图 20 所示：

  

  图20：每一列非0元素的个数

  图 2 中 array 数组表示，原稀疏矩阵中第一列有 1 个非 0 元素，第二列有 2 个非 0 元素

  。

• copt 数组用于计算稀疏矩阵中每列第一个非 0 元素在新三元组表中存放的位置。 我们通常默认第一列首个非 0 元素存放到新三元组表中的位置为 1，然后通过 cpot[col] = cpot[col-1] + array[col-1] 公式可计算出后续各列首个非 0 元素存放到新三元组表的位置。拿图 1 中的稀疏矩阵来说，它对应的 copt 数组如图 21 所示：

  

  图21：copt数组示意图

  图 21 中的 copt 数组表示，原稀疏矩阵中第 2 列首个非 0 元素存放到新三元组表的位置为 2。

注意，cpot[col] = cpot[col-1] + array[col-1] 的意思是，后一列首个非 0 元素存放的位置等于前一列首个非 0 元素的存放位置,加上该列非 0 元素的个数。由此可以看出，copt 数组才是最终想要的，而 array 数组的设立只是为了帮助我们得到 copt 数组。

稀疏矩阵快速转置算法的时间复杂度为 O(n)。即使在最坏的情况下（矩阵中全部都是非 0 元素），该算法的时间复杂度也才为 O(n2)。

---

矩阵乘法

矩阵相乘的前提条件是：乘号前的矩阵的列数要和乘号后的矩阵的行数相等。且矩阵的乘法运算没有交换律，即 AB 和 BA 是不一样的。假设下面是矩阵A：

3	0	0	5
0	-1	0	0
2	0	0	0

下面是矩阵B：

0	2
1	0
-2	4
0	0

由于矩阵 A 的列数和矩阵 B 的行数相等，可以进行 AB 运算（不能进行 BA 运算）。计算方法是：用矩阵 A 的第 i 行和矩阵 B 中的每一列 j 对应的数值做乘法运算，乘积一一相加，所得结果即为矩阵 C 中第 i 行第 j 列的值。

例如：C12 = 6 是因为：A11B12 + A12B22 + A13B32 + A14B42，即 32 + 00 + 04 + 50 = 6 ，因为这是 A 的第 1 行和 B的第 2 列的乘积和，所以结果放在 C 的第 1 行第 2 列的位置。

结果矩阵C为：

0	6
-1	0
0	4

例如，A 是 m1n1 矩阵，B 是 m2n2 矩阵(前提必须是 n1 == m2 )： 普通算法的时间复杂度为 O(m1*n2*n1)

基于行逻辑链接的顺序表的矩阵乘法

具体过程不描述，请自行百度，这里只说结论。

当稀疏矩阵 Amn 和稀疏矩阵 Bnp 采用行逻辑链接的顺序表做乘法运算时，在矩阵 A 的列数（矩阵 B 的行数） n 不是很大的情况下，算法的时间复杂度相当于 O(m*p)，比普通算法要快很多

---

矩阵加法

矩阵之间能够进行加法运算的前提条件是：各矩阵的行数和列数必须相等。

在行数和列数都相等的情况下，矩阵相加的结果就是矩阵中对应位置的值相加所组成的矩阵，例如：

图22：矩阵相加

十字链表法 过程有点复杂，具体请自行百度，这里只说结论 使用十字链表法解决稀疏矩阵的压缩存储的同时，在解决矩阵相加的问题中，对于某个单独的结点来说，算法的时间复杂度为一个常数（全部为选择结构），算法的整体的时间复杂度取决于两矩阵中非 0 元素的个数。

广义表

一、定义

广义表是线性表的推广，也称为列表。n ( >=0 )个表元素组成的有限序列，记作LS = (a0, a1, a2, …, an-1) LS是表名，ai是表元素，它可以是表 (称为子表)，可以是数据元素(称为原子)。

以下是广义表存储数据的一些常用形式：

• A = ()：A 是一个空表，其长度为0

• B = (e)：广义表 B 中只有一个原子 e。

• C = (a,(b,c,d)) ：广义表 C 的长度为2，两个元素分别为 原子a 和 子表 (b,c,d)。

• D = (A,B,C)：广义表 D 的长度为3，三个元素都是广义表，分别是A、B和C。这种表示方式等同于 D = ((),(e),(b,c,d)) 。

• E = (a,E)：广义表 E 的长度为2，这是一个递归广义表，等同于：E = (a,(a,(a,…)))。

• F=( ( ) )：广义表F长度为1，元素为空表

特点:

1. 列表是一个多层次的结构 列表的元素是可以嵌套的

2. 列表可以被其他列表共享 如：D中有A，B，C三个子表，则在D中可以不必列出子表的值，而是通过子表的名称来引用。

3. 列表可以为一个递归的表

4. 两个重要运算：

   • 取表头 GetHead(LS)：取出的表头为非空广义表的第一个元素，可以是一个原子，也可以是一个子表

   • 取表尾 GetTail(LS)：取出的表尾为除去表头之外，由其余元素构成的表。即表尾一定是一个广义表。

二、广义表存储结构

由于广义表中数据元素可以具有不同的结构，所以很难用顺序结构统一，所以一般使用链式存储结构，常用的链式存储结构有两种：头尾链表的存储和扩展线性链表的存储结构。

1.头尾链表

由于广义表的数据结构可能为原子或广义表，由此需要两种结构的结点：

• 表结点，用来表示广义表。由三个域组成：标志域、指示表头的指针域、指示表尾的指针域

• 原子结点，用以表示原子。由两个域组成：标志域和值域

 

广义表的头尾链表存储表示：

//ATOM=0表示原子，LIST=1表示子表
typedef enum{ATOM,LIST} ElemTag;
typedef struct GLNode
{
    ElemTag tag;  //公共部分，用于区分原子结点和表结点
    union  // 原子结点和表结点的联合部分
    {
        // 以下的部分根据tag二选一
        AtomType atom;  //1.atom 是原子结点的值域，AtomTupe由用户自己定义
        struct
        {
            struct *GLNode *hp;
            struct *GLNode *tp;
        }ptr;  // 2.ptr是表结点的指针域，ptr.hp和ptr.tp分别指向表头和表尾
    };
}*GList;  // 广义表类型

特点：

• 除空表的表头指针为空，对任何非空广义表，其表头指针均指向一个表结点，且该结点中的hp域指示4广义表表头，tp域指向广义表表尾

• 容易分清列表中原子和子表所在层次

• 最高层的表结点个数即为广义表的长度。

2.扩展线性链表

把广义表看成是包含 n个并列子表（原子也视为子表）的表

typedef enum
{
    ATOM，   // 0，表示原子
    LIST    // 1，表示列表
} ElemTag;
​
typedef struct GLNode
{
    ElemType tag;   // 公共部分，用于区分原子结点和表结点
    union
    {
        AtomType atom;      // 原子结点的值域
        struct GLNode *hp;  // 表结点的表头指针
    };
    struct GLNode *tp;      //相当于与线性链表的next，指向下一个结点
} *GList；