02-2Probability

2.5 联合概率分布

前面的都是单变量的概率分布,接下来要看看更难的,就是联合概率分布( joint probability distributions),其中要涉及到多个相关联的随机变量,实际上这也是本书的核心内容.

联合概率分布的形式是$p(x_1,...,x_D)$,这些随机变量属于一个规模为 D>1 的集合,对这些随机变量间的(随机stochastic)关系进行建模,就要用联合概率分布.如果所有变量都是离散的,那就可以把联合分布表示成一个大的多维数组,每个维度对应一个变量.若设每个变量的状态数目总共是 K, 那么这样要建模的话,需要定义的参数个数就达到了$O(K^D)$了.

2.5.1 协方差和相关系数

协方差(covariance)是用来衡量两组变量之间(线性)相关的程度的,定义如下:

$cov[X,Y]\stackrel{△}{=}E[(X-E[X])(Y-E[Y])]=E[XY]-E[X]E[Y]$(2.65)

此处查看原书图2.12

如果 x 是一个 d 维度的随机向量,那么它的协方差矩阵(covariance matrix) 的定义如下所示,这是一个对称正定矩阵(symmetric positive definite matrix):

c o v [ x ] ∗ = E [ ( x − E [ x ] ) ( x − E [ x ] ) T ]  (2.66) = ( v a r [ X 1 ] c o v [ X 1 , X 2 ] . . . c o v [ X 1 , X d ] c o v [ X 2 , X 1 ] v a r [ X 2 ] . . . c o v [ X 2 , X d ] . . . . . . . . . . . . c o v [ X d , X 1 ] c o v [ X d , X 2 ] . . . v a r [ X d ] )  (2.67) \begin{aligned} cov[x]*&= E[(x-E[x])(x-E[x])^T] \text{ (2.66)}\\ &= \begin{pmatrix} var[X_1] & cov[X_1,X_2] &...& cov[X_1,X_d] \\ cov[X_2,X_1] & var[X_2] &...&cov[X_2,X_d] \\ ...&...&...&...\\ cov[X_d,X_1] & cov[X_d,X_2] &...&var[X_d] \\ \end{pmatrix} \text{ (2.67)}\\ \end{aligned} cov[x]∗​=E[(x−E[x])(x−E[x])T] (2.66)= ​var[X1​]cov[X2​,X1​]...cov[Xd​,X1​]​cov[X1​,X2​]var[X2​]...cov[Xd​,X2​]​............​cov[X1​,Xd​]cov[X2​,Xd​]...var[Xd​]​ ​ (2.67)​

协方差可以从0到$\infty $之间取值.有时候为了使用方便,会将其正规化为有上限.

两个变量X 和 Y 之间的(皮尔逊)相关系数(correlation coefficient)定义如下:

$corr[X,Y]\stackrel{△}{=}\frac{cov[X,Y]}{\sqrt{var[X]var[Y]}}$(2.68)

而相关矩阵(correlation matrix)则为:

R = ( c o v [ X 1 , X 1 ] c o v [ X 1 , X 2 ] . . . c o v [ X 1 , X d ] . . . . . . . . . . . . c o v [ X d , X 1 ] c o v [ X d , X 2 ] . . . v a r [ X d ] ) R= \begin{pmatrix} cov[X_1,X_1] & cov[X_1,X_2] &...& cov[X_1,X_d] \\ ...&...&...&...\\ cov[X_d,X_1] & cov[X_d,X_2] &...&var[X_d] \\ \end{pmatrix} R= ​cov[X1​,X1​]...cov[Xd​,X1​]​cov[X1​,X2​]...cov[Xd​,X2​]​.........​cov[X1​,Xd​]...var[Xd​]​ ​(2.69)

从练习4.3可知相关系数是在[-1,1]这个区间内的,因此在一个相关矩阵中,每一个对角线项值都是1,其他的值都是在[-1,1]这个区间内.

另外还能发现的就是当且仅当有参数 a 和 b 满足$Y=aX+b$的时候,才有$corr [X, Y ] = 1 $,也就是说 X 和 Y 之间存在线性关系,参考练习4.3.

根据直觉可能有人会觉得相关系数和回归线的斜率有关,比如说像$Y=aX+b$这个表达式当中的系数 a 一样.然而并非如此,如公式7.99中所示,实际上回归系数的公式是$a=cov[X,Y]/var[X]$.可以将相关系数看做对线性程度的衡量,参考图2.12.

回想本书的2.2.4,如果 X 和 Y 相互独立,则有$p(X,Y)=p(X)p(Y)$,这样二者的协方差$cov[X,Y]=0$,相关系数$corr[X,Y]=0$, 很好理解,相互独立就是不相关了.但反过来可不成立,不相关并不能意味着相互独立.例如设$X\sim U(-1,1),Y=X^2$. 很明显吧,这两个是相关的对不对,甚至 Y 就是 X 所唯一决定的,然而如练习4.1所示,这两个变量的相关系数算出来等于零啊,即$corr[X,Y]=0$.图2.12有更多直观的例子,都是两个变量 X 和 Y 显著具有明显的相关性,而计算出来的相关系数却都是0.实际上更通用的用来衡量两组随机变量之间是否独立的工具是互信息量(mutual information),这部分在本书2.8.3当中有设计.如果两个变量真正不相关,这个才会等于0.

此处查看原书图2.13

2.5.2 多元高斯分布

多元高斯分布(multivariate Gaussian)或者所谓多元正态分布(multivariate normal,缩写为MVN),是针对连续随机变量的联合概率分布里面用的最广的.在第四章会对其进行详细说明,这里只说一些简单定义并且给个函数图像瞅瞅.

在 D 维度上的多元正态分布(MVN)的定义如下所示:
$N(x|\mu ,\Sigma )\stackrel{△}{=}\frac{1}{(2\pi {)}^{\frac{D}{2}}|\Sigma {|}^{\frac{1}{2}}}\exp [-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )]$(2.70)

上式中$\mu =E[x]\in R^D$是均值向量,而$\Sigma =cov[x]$ 一个$D\times D$的协方差矩阵.有时候我们会用到一个名词叫做精度矩阵(precision/concentration matrix),这个就是协方差矩阵的逆矩阵而已,也就是$\Lambda ={\Sigma }^{-1}$.前面那一团做分母的$(2\pi {)}^{\frac{D}{2}}|\Sigma {|}^{\frac{1}{2}}$也还是归一化常数,为了保证这个概率密度函数的积分等于1,更多参考练习4.5

图2.13展示了一些多元正态分布的密度图像,其中有三个是三个不同协方差矩阵的下的二维投影,另外一个是立体的曲面图像.一个完整的协方差矩阵有$D(D+1)/2$个参数,除以2是因为矩阵$\Sigma$是对称的.对角协方差矩阵的方向有 D 个参数,非对角线位置的元素的值都是0. 球面(spherical)或者各向同性(isotropic)协方差矩阵$\Sigma ={\delta }^2{I}_D$有一个自由参数.

2.5.3 多元学生 T 分布

相比多元正态分布 MVN, 多元学生T 分布更加健壮,其概率密度函数为:

$$\begin{array}{rlr}\Gamma (x|\mu ,\Sigma ,v)& =\frac{\Gamma (v/2+D/2)}{\Gamma (v/2+D/2)}\frac{|\Sigma {|}^{-1/2}}{v^{D/2}{\pi }^{D/2}}\times [1+\frac{1}{v}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu ){]}^{-(\frac{v+D}{2})}& \text{ (2.71)}\\ & =\frac{\Gamma (v/2+D/2)}{\Gamma (v/2+D/2)}|\pi V{|}^{-1/2}\times [1+(x-\mu {)}^T{\Sigma }^{-1}(x-\mu ){]}^{-(\frac{v+D}{2})}& \text{ (2.72)}\end{array}$$

其中的$\Sigma$叫做范围矩阵(scale matrix),而并不是真正的协方差矩阵,$V=v\Sigma$.这个分布比高斯分布有更重的尾部(fatter tails).参数$v$越小,越重尾;而当$v\to \infty$则这个分布趋向为高斯分布.这个分布的属性如下所示:

$mean=\mu ,mode=\mu ,Cov=\frac{v}{v-2}\Sigma$(2.73)

2.5.4 狄利克雷分布

$\beta$分布扩展到多元就成了狄利克雷分布(Dirichlet distribution),支持概率单纯形(probability simplex),定义如下:

$S_K=x:0\le x_k\le 1,{\sum }_{k=1}^K{x}_k=1$(2.74)

其概率密度函数 pdf 如下所示:

$Dir(x|\alpha )\stackrel{△}{=}\frac{1}{B(\alpha )}{\prod }_{k=1}^K{x}_k^{{\alpha }_k-1}\prod (x\in S_K)$(2.75)

此处查看原书图2.14

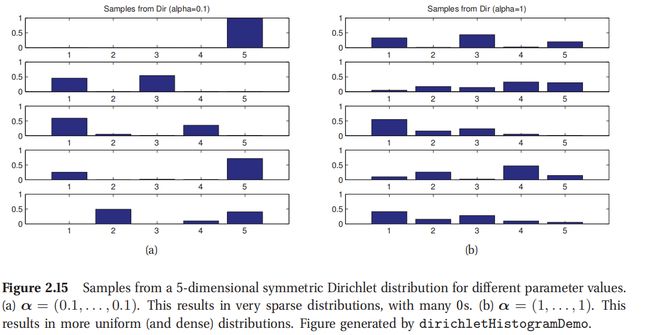
此处查看原书图2.15

上式中的$B({\alpha }_1,...,{\alpha }_K)$是将$\beta$函数在 K 个变量上的自然推广(natural generalization),定义如下:

$B(\alpha )\stackrel{△}{=}\frac{{\prod }_{k=1}^K\Gamma ({\alpha }_k)}{\Gamma ({\alpha }_0)}$(2.76)
其中的${\alpha }_0\stackrel{△}{=}{\sum }_{k=1}^K{\alpha }_k$.

图2.14展示的是当 K=3的时候的一些狄利克雷函数图像,图2.15是一些概率向量样本.很明显其中${\alpha }_0\stackrel{△}{=}{\sum }_{k=1}^K{\alpha }_k$控制了分布强度,也就是峰值位置.例如Dir(1, 1, 1)是一个均匀分布,Dir(2, 2, 2) 是以为(1/3, 1/3, 1/3)中心的宽分布(broad distribution),而Dir(20, 20, 20) 是以为(1/3, 1/3, 1/3)中心的窄分布(narrow distribution).如果对于所有的 k 都有${\alpha }_k<1$,那么峰值在单纯形的角落.

这个分布的属性如下:
$E[x_k]=\frac{{\alpha }_k}{{\alpha }_0},mode[x_k]=\frac{{\alpha }_k-1}{{\alpha }_0-K},var[x_k]=\frac{{\alpha }_k({\alpha }_0-{\alpha }_k)}{{\alpha }_0^2({\alpha }_0+1)}$(2.77)

上式中的${\alpha }_0={\sum }_k{\alpha }_k$.通常我们用对称的狄利克雷分布,${\alpha }_k=\alpha /K$. 这样则有方差$var[x_k]=\frac{K-1}{K^2(\alpha +1)}$. 这样增大$\alpha$就能降低方差,提高了模型精度.

2.6 随机变量变换

如果有一个随机变量$x\sim p()$,还有个函数$y=f(x)$,那么 y 的分布是什么?这就是本节要讨论的内容.

2.6.1 线性变换

设$f()$是一个线性函数:
$y=f(x)=Ax+b$(2.78)

这样就可以推导 y 的均值和协方差了.首先算均值如下:
$E[y]=E[Ax+b]=A\mu +b$(2.79)

上式中的$\mu =E[x]$.这就叫线性期望(linearity of expectation).如果$f()$ 是一个标量值函数(scalar-valued function)$f(x)=a^Tx+b $,那么对应结果就是:

$E[a^{T}x+b]=a^T\mu +b$(2.80)

对于协方差,得到的就是:

$cov[y]=cov[Ax+b]=A\Sigma A^T$(2.81)

其中的$\Sigma =cov[x]$, 这个证明过程留作联系.如果$f()$ 是一个标量值函数(scalar-valued function),这个结果就成了:
$var[y]=var[a^{T}x+b]=a\Sigma a^T$(2.82)

这些结果后面的章节都会多次用到.不过这里要注意,只有x 服从高斯分布的时候,才能单凭借着均值和协方差来定义 y 的分布.通常我们必须使用一些技巧来对 y 的完整分布进行推导,而不能只靠两个属性就确定.

2.6.2 通用变换

如果 X 是一个离散随机变量, $f(x)=y$, 推导 y 的概率质量函数 pmf,只要对所有x 的概率值了加到一起就可以了, 如下所示:
$p_y(y)={\sum }_{x:f(x)=y}{p}_x(x)$(2.83)

例如,若X是偶数则$f(X)=1$,奇数则$f(X)=0$,$p_x(X)$是在集合$\{1,...,10\}$上的均匀分布(uniform),这样$p_y(1)=x\in \{2,4,6,8,10\},p_x(x)=0.5,p_y(0)=0.5$.注意这个例子中的函数 f 是多对一的函数.
如果 X 是连续的随机变量,就可以利用公式2.83,因为$p_x(x)$是一个密度,而不是概率质量函数了,也就不能把密度累加起来了. 这种情况下用的就是连续密度函数 cdf 了,协作下面的形式:

$P_y(y)\stackrel{△}{=}P(Y\le y)=P(f(X)\le y)=P(X\in \{x|f(x)\le y\})$(2.84)

对连续密度函数 cdf 进行微分,就能得到概率密度函数 pdf 了:

$P_y(y)\stackrel{△}{=}P(Y\le y)=P(X\le f^{-1}(y))=P_x(f^{-1}(y))$(2.85)

求导就得到了:

$p_y(y)\stackrel{△}{=}\frac{d}{dy}{P}_y(y)=\frac{d}{dy}{P}_x(f^{-1}(y)=\frac{dx}{dy}\frac{d}{dx}P-X(x)=\frac{dx}{dy}px(x)$(2.86)

显然 $x=f^{-1}(y)$ ,可以把 $dx$看作是对 x 空间的一种体测量;类似的把$dy$当作对 y 空间体积的测量.这样$\frac{dx}{dy}$就测量了体积变化.由于符号无关紧要,所以可以取绝对值来得到通用表达式:

$p_y(y)=p_x(x)|\frac{dx}{dy}|$(2.87)

这也叫变量转换公式(change of variables formula).按照下面的思路来理解可能更容易.落在区间$(x,x+\delta x)$的观测被变换到区间$(y,y+\delta y)$ , 其中$p_x(x)\delta x\approx p_y(y)\delta y$.因此$p_y(y)approx{p}_x(x)|\frac{\delta x}{\delta y}|$.例如,假如有个随机变量$X\sim U(-1,1),Y=X^2$.那么则有$p_y(y)=\frac{1}{2}{y}^{-\frac{1}{2}}$. 具体看练习2.10.

2.6.2.1 变量的多重变化(Multivariate change of variables)

前面的结果可以推到多元分布上.设$f$是一个函数,从$R^n$映射到$R^n$, 设$y=f(x)$. 那么就有这个函数的雅可比矩阵 J(Jacobian matrix):

J x → y ∗ = ∂ ( y 1 , . . . , y n ) ∂ ( x 1 , . . . , x n ) = △ ( ∂ y 1 ∂ x 1 . . . ∂ y 1 ∂ x n . . . . . . . . . ∂ y n ∂ x 1 . . . ∂ y n ∂ x n ) J_{x\rightarrow y } * = \frac{\partial(y_1,...,y_n)}{\partial(x_1,...,x_n)}\overset\triangle{=} \begin{pmatrix} \frac{\partial y_1}{\partial x_1} & ...& \frac{\partial y_1}{\partial x_n} \\ ...&...&...\\ \frac{\partial y_n}{\partial x_1} &...&\frac{\partial y_n}{\partial x_n} \\ \end{pmatrix} Jx→y​∗=∂(x1​,...,xn​)∂(y1​,...,yn​)​=△ ​∂x1​∂y1​​...∂x1​∂yn​​​.........​∂xn​∂y1​​...∂xn​∂yn​​​ ​(2.88)

矩阵 J 的行列式|det J|表示的是在运行函数 f 的时候一个单位的超立方体的体积变化.
如果 f 是一个可逆映射(invertible mapping),就可以用逆映射$y\to x$的雅可比矩阵(Jacobian matrix) 来定义变换后随机变量的概率密度函数(pdf)

$p_y(y)=p_x(x)|det(\frac{\partial x}{\partial y})|=p_x(x)|det{J}_{y\to x}$(2.89)
在练习4.5,你就要用到上面这个公式来推导一个多元正态分布的归一化常数(normalization constant).

举个简单例子,假如要把一个概率密度函数从笛卡尔坐标系(Cartesian coordinates)的$x=(x_1,x_2)$ 转换到一个极坐标系(polar coordinates)$y=(r,\theta )$, 其中有对应关系:$x_1=r\cos \theta ,x_3=r\sin \theta$.这样则有雅可比矩阵如下:

$$J_{y\to x}=\left(\begin{array}{cc}\frac{\partial x_1}{\partial r}& \frac{\partial x_1}{\partial \theta }\\ \frac{\partial x_2}{\partial r}& \frac{\partial x_2}{\partial \theta }\end{array}\right)=\left(\begin{array}{cc}\cos \theta & -r\sin \theta \\ \sin \theta & r\cos \theta \end{array}\right)$$(2.90)

矩阵 J 的行列式为:

$|detJ|=|r{\cos }^2\theta +r{\sin }^2\theta |=|r|$(2.91)

因此:

$p_y(y)=p_x(x)|detJ|$(2.92)

$p_{r,\theta }(r,\theta )=p_{x_1,x_2}(x_1,x_2)r=p_{x_1,x_2}(r\cos \theta ,r\sin \theta )r$(2.93)

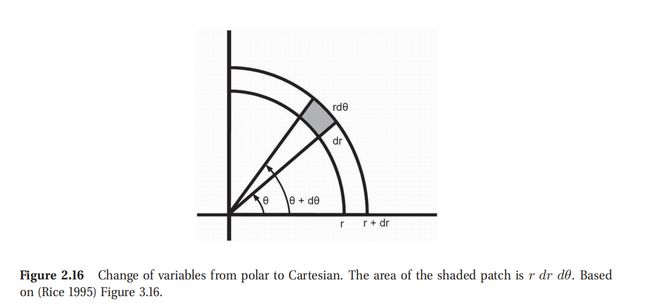
以几何角度来看,可以参考图2.16,其中的阴影部分面积可以用如下公式计算:

$P(r\le R\le r+dr,\theta \le \Theta \le \theta +d\theta )=p_{r,\theta }(r,\theta )drd\theta$(2.94)

在这个限制范围内,这也就等于阴影中心部分的密度$p(r,\theta )$乘以阴影部分的面积,$rdrd\theta$.因此则有:

$p_{r,\theta }(r,\theta )drd\theta =p_{x_1,x_2}(r\cos \theta ,r\sin \theta )rdrd\theta$$(2.95)

此处查看原书图2.16

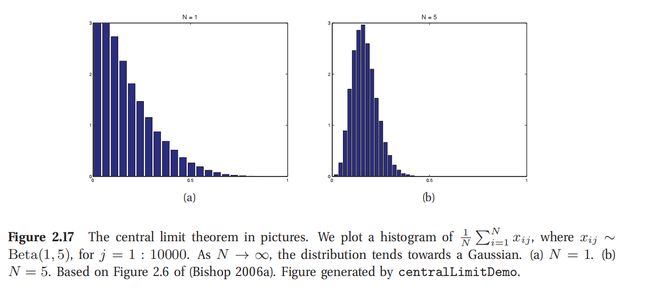
此处查看原书图2.17

2.6.3 中心极限定理(Central limit theorem)

现在设想有 N 个随机变量,概率密度函数(pdf)为p(x_i),且不一定是正态分布,每个的均值和方差都分别是$\mu ,{\sigma }^2$.然后假设每个随机变量都是独立同分布的(independent and identically distributed,缩写成iid).设$S_N={\sum }_{i=1}^N{X}_i$是所有随机变量的和.这是一个很简单的变换,但应用很广.随着 N 的增大,这个和的分布会接近:

$p(S_N=s)=\frac{1}{\sqrt{2\pi N{\sigma }^2}}\exp (-\frac{(s-N\mu {)}^2}{2N{\sigma }^2})$(2.96)

所以这个量的分布就是:

$Z_N\stackrel{△}{=}\frac{S_N-N_{\mu }}{\sigma \sqrt{N}}=\frac{\bar{X}-\mu }{\sigma /\sqrt{N}}$(2.97)

这个分布就会收敛到标准正态分布了,其中样本均值为:$\bar{X}=\frac{1}{N}{\sum }_{i=1}^N{x}_i$.这就叫做中心极限定理,更多内容参考(Jaynes 2003, p222) 或者 (Rice 1995, p169).

图2.17即是一例,其中计算$\beta$分布变量均值,右图可见很快收敛到正态分布了.

2.7 蒙特卡罗近似方法(Monte Carlo approximation)

要计算一个随机变量的函数的分布,靠公式变换 通常还挺难的.有另外一个办法,简单又好用.首先就是从分布中生成 S 个样本,就把它们标为$x_1,...,x_S$.生成样本有很多方法,对于高维度分布来说最流行的方法就是马尔科夫链蒙特卡罗方法(Markov chain Monte Carlo,缩写为 MCMC),这部分内容在本书24章再行讲解.
还说这个例子,对分布函数$f(X)$使用经验分布(empirical distribution)$\{f(x_s){\}}_{s=1}^S$来进行近似.这就叫蒙特卡洛近似(Monte Carlo approximation), 之所以用这个名字是因为欧洲的知名赌城.这种方法首先是在统计物理里面应用发展起来的,确切来说还是在原子弹研究过程中,不过现在已经广泛应用在统计和机器学习领域里面了.

此处查看原书图2.18

应用蒙特卡罗方法,可以对任意的随机变量的函数进行近似估计.先简单取一些样本,然后计算这些样本的函数的算术平均值(arithmetic mean).这个过程如下所示:

$E[f(X)]=\int f(xp(x)dx\approx \frac{1}{S}{\sum }_{s=1}^{S}f(x_s)$(2.98)

上式中$x_s\sim p(X)$.这就叫做蒙特卡罗积分(Monte Carlo integration),相比数值积分(numerical integration)的一个优势就是在蒙特卡罗积分中只在具有不可忽略概率的地方进行评估计算,而数值积分会对固定网格范围内的所有点的函数进行评估计算.

通过调整函数$f()$,就能对很多有用的变量进行估计,比如:

• $\bar{x}=\frac{1}{S}{\sum }_{s=1}^S{x}_s\to E[X]$
• $\frac{1}{S}{\sum }_{s=1}^S(x_s-\bar{x}{)}^2\to var[X]$
• $\frac{1}{S}\#\{x_s\le c\}\to P(X\le c)$
• 中位数(median)$\{x_1,...,x_S\}\to median(X)$

下面是一些例子,后面一些章节有更详细介绍.

2.7.1 样例:更改变量,使用 MC (蒙特卡罗)方法

在2.6.2，我们讨论了如何分析计算随机变量函数的分布$y=f(x)$.更简单的方法是使用蒙特卡罗方法估计.例如,若$x\sim Unif(-1,1),y=x^2$.就可以这样估计$p(y)$:从 $p(x)$ 中去多次取样,取平方,计算得到的经验分布.如图2.18所示.后文中还要广泛应用这个方法.参考图5.2.

此处查看原书图2.19

2.7.2 样例:估计圆周率$\pi$,使用蒙特卡罗积分

蒙特卡罗方法还可以有很多种用法,不仅仅是统计学领域.例如我们可以用这个方法来估计圆周率$\pi$.我们知道圆的面积公式可以利用圆周率和圆的半径 r 来计算,就是$\pi r^2$,另外这个面积也等于下面这个定积分(definite integral):
$I={\int }_{-r}^r{\int }_{-r}^r\prod (x^2+y^2\le r^2)dxdy$(2.99)

因此有 $\pi =I/(r^2)$.然后就可以用蒙特卡罗积分来对此进行近似了.设$f(x,y)=\prod (x^2+y^2\le r^2)$是一个指示器函数(indicator function),只要点在圆内,则函数值为1,反之为0,然后设$p(x),p(y)$都是在闭区间[-r,r]上的均匀分布(uniform distribution),所以有$p(x)=p(y)=\frac{1}{2r}$ 这样则有:

$$\begin{array}{rlr}I& =(2r)(2r)\int \int f(x,y)p(x)p(y)dxdy& \text{ (2.100)}\\ & =4r^2\int \int f(x,y)p(x)p(y)dxdy& \text{ (2.101)}\\ & =4r^2\frac{1}{S}\sum _{s=1}^{S}f(x_s,y_s)& \text{ (2.102)}\end{array}$$

当标准差为0.09的时候,计算得到的圆周率为$\hat{\pi }=3.1416$,参考本书2.7.3就知道什么是标准差了.接受/拒绝的点如图2.19中所示.

此处查看原书图2.20

2.7.3 蒙特卡罗方法的精确度

随着取样规模的增加,蒙特卡罗方法的精度就会提高,如图2.20所示,在图上部是从一个高斯分布中取样的直方图,底下的两个图使用了核密度估计(kernel density estimate, 参考本书14.7.2)得到的光滑曲线.这种光滑分布函数在密集网格点上进行评估和投图.这里要注意一点,光滑操作只是为了投图看而已,蒙特卡罗方法估计的过程根本用不着光滑.
如果我们知道了均值的确切形式,即$\mu =E]f(X)]$,然后蒙特卡罗方法近似得到的是$\hat{\mu }$,那么对于独立取样则有:
$(\hat{\mu }-\mu )\to N(0,\frac{{\sigma }^2}{S})$(2.103)

其中:
${\sigma }^2=var[f(X)]=E[f(X{)}^2]-E[f(X){]}^2$(2.104)

这是由中心极限定理决定的.当然了,上式中的${\sigma }^2$是位置的,但也可以用蒙特卡罗方法来估计出来:
${\hat{\sigma }}^2=\frac{1}{S}{\sum }_{s=1}^S(f(x_s)-\hat{\mu }{)}^2$(2.105)

然后则有:
$P\{\mu -1.96\frac{\hat{\sigma }}{\sqrt{S}}\le \hat{\mu }\le \mu +1.96\frac{\hat{\sigma }}{\sqrt{S}}\}\approx 0.95$(2.106)

上式中的$\frac{\hat{\sigma }}{\sqrt{S}}$就叫做数值标准差或者经验标准差(numerical or empirical standard error), 这个量是对我们对$\mu$估计精度的估计.具体信息查看本书6.2有更多讲解.

如果我们希望得到的答案$\pm ϵ$范围内的概率至少为95%,那就要保证取样数目 S 满足条件 $1.96\sqrt{{\hat{\sigma }}^2/S}\le ϵ$, 这里的1.96可以粗略用2替代,这样就得到了$S\ge \frac{4{\hat{\sigma }}^2}{{ϵ}^2}$.

2.8 信息理论

信息理论(information theory)关注的是以紧凑形式进行数据呈现(这种紧凑形式也被称为数据压缩(data compression)或者源编码(source coding)),以及以能健壮应对错误的方式进行传输和存储(这个过程也叫做纠错(error correction) 或者信道编码(channel coding)).第一眼看上去好像这和概率论以及机器学习没什么关系,不过实际是有联系的.首先,对数据进行紧凑表达需要给高概率的字符串赋予短编码字,而将长编码字留给低概率字符串.就好比自然语言中,特别常用的词汇都往往比少见的词汇短很多,比如冠词 a/the 明显比闪锌矿 sphalerite 短很多.另外,在噪音频道上进行信息解码也需要对人发送的不同信息建立一个良好的概率模型.这就都需要一个能够预测数据可能性的模型,这也是机器学习里面的一个核心问题,关于信息理论和机器学习之间关系的更多内容请参考(MacKay 2003).

显然这里不可能说太多太深关于信息理论的内容,有兴趣的话去看(Cover and Thomas 2006).这里也就是介绍本书中要用到的一些基础概念了.

2.8.1 信息熵

随机变量 X 服从分布 p, 这个随机变量的熵(entropy)则表示为$H(X)$或者$H(p)$,这是对随机变量不确定性的一个衡量.对于一个有 K 个状态的离散随机变量来说,其信息熵定义如下:

$H(X)\stackrel{△}{=}-{\sum }_{k=1}^{K}p(X=k){\log }_{2}p(X=k)$(2.107)

通常都用2作为对数底数,这样单位就是 bit (这个是 binary digits 的缩写).如果用自然底数 e, 单位就叫做 nats 了.
举个例子,$X\in \{1,...,5\}$,柱状分布(histogram distribution), 概率$p=[0.25,0.25,0.2,0.15,0.15]$,利用上面的公式计算得到$H=2.2855$.
熵最大的离散分布就是均匀分布,可以参考本书9.2.6.因为对于一个 K 元(K-ary)随机变量,如果$p(x=k)=1/K$,则信息熵最大,这时候的熵为$H(X)={\log }_{2}K$. 熵最小的分布就是所有概率质量都在单一状态的$\delta$分布,这时候熵为0,因为只有一个状态有概率,没有任何不确定性.

在图2.5当中对 DNA 序列进行了投图,每一列的高度定义为$2-H$,其中的 H 就是这个分布的熵,2是最大可能熵(maximum possible entropy).因此高度为0的就表示均匀分布,而高度为2就对应着确定性分布(deterministic distribution).

此处查看原书图2.21

对于二值化随机变量的特例,$X\in \{0,1\}$,则有$p(X=1)=\theta ,p(X=0)=1-\theta$,这样熵为:

$$\begin{array}{rlr}H(X)& =-[p(X=1){\log }_{2}p(X=1)+p(X=0){\log }_{2}p(X=0)]& \text{(2.108)}\\ & =-[\theta {\log }_2\theta +(1-\theta ){\log }_2(1-\theta )]& \text{(2.109)}\end{array}$$

这也叫做二值熵函数(binary entropy function),也写作$H(\theta )$,如图2.21所示,可见当$\theta =0.5$的时候熵值最大为1,这时候是均匀分布了.

2.8.2 KL 散度

KL 散度(Kullback-Leibler divergence),也称相对熵(relative entropy),可以用来衡量p和q两个概率分布的差异性(dissimilarity).定义如下:

$KL(p||q)\stackrel{△}{=}{\sum }_{k=1}^K{p}_k\log \frac{p_k}{q_k}$(2.110)

上式中的求和也可以用概率密度函数的积分来替代.就可以写成:

$KL(p||q)={\sum }_k{p}_k\log p_k-{\sum }_k{p}_k\log q_k=-H(p)+H(p,q)$(2.111)

上式中的$H(p,q)$就叫做交叉熵(cross entropy):

$H(p,q)\overset\triangle{=}-\sum_kp_k\log q_k $(2.112)

参考 (Cover and Thomas 2006) 可以证明,当使用模型 q 来定义编码本(codebook)的时候,来自分布 p 的待编码数据的平均比特数(average number of bits)就是交叉熵.正规熵(regular entropy)$H(p)=H(p,p)$,参考本书2.8.1的定义,也就是使用真实模型时候的比特数期望值,因此 KL 散度也就是不同概率分布之间的不同的量度.换个说法, KL 散度就是要对数据编码所需要的额外比特(extra bits)的平均数,因为这时候用分布 q 来对数据进行编码,而不是使用分布 p.

既然是额外的比特数,这种表述就很明显说明这个 KL 散度应该是非负的,即$KL(p||q)\ge 0$,等于0则意味着两个分布相等,即$p=q$.接下来对此进行一下证明.

定理2.8.1 信息不等式(Information inequality)

$KL(p||q)\ge 0$ 当且仅当 $p=q$的时候, KL 散度为0.

证明

要证明这个定理,需要用到詹森不等式(Jensen’s inequality).这个不等式是说,对于任意的凸函数(convex function) f,有以下关系:

$f({\sum }_{i=1}^n{\lambda }_i(x_i))\le {\sum }_{i=1}^n{\lambda }_{i}f(x_i)$(2.113)

其中${\lambda }_i\ge 0,{\sum }_{i=1}^n{\lambda }_i=1$. 由于凸函数的定义,对于 n=2的时候很显然,对于 n>2 的情况也可以归纳证明(proved by induction).

对定理的证明参考了(Cover and Thomas 2006, p28).设$A=\{x:p(x)>0\}$是$ p(x)$ 的支撑集合(support, 译者注:纯白或许就当做定义域理解好了).则有:

$$\begin{array}{rlr}-KL(p||q)& =-\sum _{x\in A}p(x)\log \frac{p(x)}{q(x)}=\sum _{x\in A}p(x)\log \frac{q(x)}{p(x)}& \text{(2.114)}\\ & \le \sum _{x\in A}p(x)\frac{q(x)}{p(x)}=\log \sum _{x\in A}q(x)& \text{(2.115)}\\ & \le \log \sum _{x\in \chi }q(x)=\log 1=0& \text{(2.116)}\end{array}$$
当 上面第一个不等式是应用了詹森不等式.因为$\log (x)$是个严格凸函数,所以在等式2.115里面,当且仅当对于某些 c 使$p(x)=cq(x)$成立的时候,等量关系成立.等式2.116中的等量关系当且仅当${\sum }_{x\in A}q(x)={\sum }_{x\in \chi }q(x)=1$的时候成立,这时候 c=1. 所以对于所有的 x 来说,当且仅当$p(x)=q(x),KL(p||q)=0$.

证明完毕.

这个结果的一个重要推论就是具有最大熵的离散分布就是均匀分布.更确切地说,$H(X)\le \log |\chi |$,$|\chi |$是 X 的状态数,当且仅当$p(x)$是均匀分布的时候等号成立.设$u(x)=1/|\chi |$,则有:
$$\begin{array}{rlr}0& \le KL(p||u)=\sum _{x}p(x)\log \frac{p(x)}{u(x)}& \text{(2.116)}\\ & =\sum _{x}p(x)\log p(x)-\sum _{x}p(x)\log u(x)=-H(X)+\log |\chi |& \text{(2.118)}\end{array}$$

上面这个就是公式化的拉普拉斯不充分理由原则(Laplace’s principle of insufficient reason),说的是在没理由优先选择某个分布的时候,优先选择均匀分布(uniform distribution).关于如何建立满足特定约束条件(certain constraints) 的分布可以阅读本书9.2.6,其他方面尽可能最小化(as least-commital as possible).(正态分布满足一阶和二阶矩约束条件,但其他方面有最大熵.)

2.8.3 信息量(Mutual information)

设有两个随机变量 X 和 Y. 如果我们想知道一个变量告诉我们关于另一个变量的多少信息。就可以计算相关系数(correlation coefficient)了,可是相关系数只适用于实数值的随机变量.另外相关系数对不相关程度的衡量作用也很有限,如图2.12所示.所以更常用的方法是对比联合分布(joint distribution)$p(X,Y)$和因式分布(factored distribution)$p(X)p(Y)$的相关性.这就叫互信息量(mutual information) 或者简写做 MI, 定义如下:
$I(X;Y)\stackrel{△}{=}KL(p(X,Y)||p(X)p(Y))={\sum }_x{\sum }_{y}p(x,y)\log \frac{p(x,y)}{p(x)p(y)}$(2.119)

$I(X;Y)\ge 0$的等号当且仅当$p(X,Y)=p(X)p(Y)$的时候成立.也就是如果两个变量相互独立,则互信息量 MI 为0. 为了深入理解 MI 这个量的含义,咱们用联合和条件熵的方式来重新表述一下.参考练习2.12可以得到上面的表达式等价于下列形式:

$I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)$(2.120)

上式中的$H(Y|X)$就是条件熵(conditional entropy) 定义为$H(Y|X)={\sum }_{x}p(x)H(Y|X=x)$.这样就可以把 X 和 Y 之间的互信息量 MI 理解成在观测了 Y 之后对 X 的不确定性的降低,或者反过来就是观测了 X 后对 Y 不确定性的降低.本书后面一些内容中还会用到这个概念.参考2.13和2.14来阅读互信息量 MI 和相关系数之间的联系.

另外一个和互信息量 MI 有很密切联系的量是点互信息量(pointwise mutual information,缩写为 PMI), 对于两个事件(而不是随机变量) x 和 y,其点互信息量 PMI 定义如下:

$PMI(x,y)\stackrel{△}{=}\log \frac{p(x,y)}{p(x)p(y)}=\log \frac{p(x|y)}{p(x)}=\log \frac{p(y|x)}{p(y)}$(2.121)

这个量衡量的是与偶发事件相比,这些事件之间的差异.很明显 X 和 Y 的互信息量 MI 就是点互信息量 PMI 的期望值.所以就可以把点互信息量 PMI 的表达式写为:

$PMI(x,y)=\log \frac{p(x|y)}{p(x)}=\log \frac{p(y|x)}{p(y)}$(2.122)

这个量是通过将先验(prior)的 $p(x)$ 更新到后验(posterior)的$p(x|y)$得到的,也可以是将先验的 $p(y)$ 更新到后验的$p(y|x)$得到.

2.8.3.1 连续随机变量的互信息量

上一节中的互信息量 MI 定义是针对离散随机变量的.对于连续随机变量,可以先对其进行离散化(discretize)或者量子化(quantize),具体方法可以使将每个随机变量归类到一个区间里面,将变量的变化范围划分出来,然后计算每一段的小区间中的分布数量(Scott 1979).然后就可以利用上文的方法公式来计算互信息量 MI 了(代码参考PMTK3的 mutualInfoAllPairsMixed, 样例可以参考miMixedDemo).

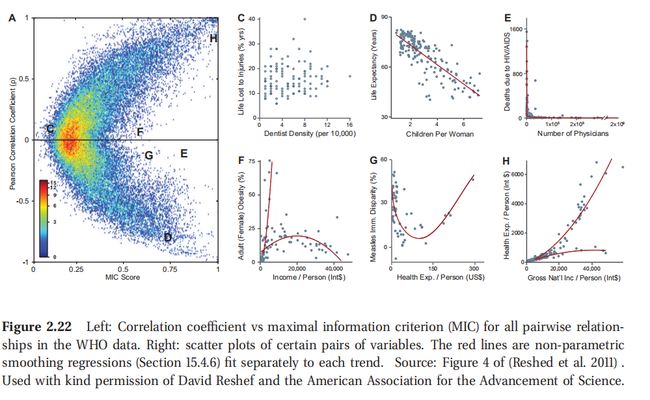
此处查看原书图2.22

然而很不幸,分成多少个小区间,以及小区间边界的位置,都可能对计算结果有很大影响.一种解决方法就是直接对互信息量 MI 进行估计,而不去先进行密度估计(Learned-Miller 2004)).另一种办法是尝试很多不同的小区间规模和位置,然后计算得到的最大互信息量 MI.经过适当的标准化之后,这个统计量就被称为最大信息系数(maximal information coefficient,缩写为 MIC)(Reshed et al. 2011).更确切来说定义如下所示:

$m(x,y)=\frac{{\max }_{G\in G(x,y)}I(X(G);Y(G))}{\log \min (x,y)}$(2.123)

上式中的$G(x,y)$是一个规模为$ x\times y$ 的二维网状集合,而$X(G),Y(G)$表示的是将变量在这个网格上进行离散化得到的结果.在区间位置(bin locations)上最大化的过程可以通过使用动态编程(dynamic programming)来有效进行(Reshed et al. 2011).这样定义了连续变量互信息量 MIC如下:

$MIC\stackrel{△}{=}{\max }_{x,y:xy<B}m(x,y)$(2.124)

上式中的 B 是一个与取样规模相关的约束条件,用于约束能使用且能可靠估计分布的区间个数. ((Reshed et al. 2011) 建议的是$B=N^{0.6}$.显然 MIC 处于区间[0, 1]中,其中-表示两个变量没关系,而1表示二者有无噪音的相关性(noise-free relationship),这种相关性可以是任意形式的,不仅仅是线性相关.

图2.22给出的是一个实例.其中的数据集包含了357个变量,衡量一系列的社会/经济/健康/政治指标,由世界健康组织 WHO 手机.左边的途中看到了对于 65,566 个变量对的相关系数(CC)与互信息量(MIC)的关系图.有图则投了一些特定变量对的散点图,其中包括了:

• C 图中的是 CC 和 MIC 都低,相应的散点图很明显表明了这两组变量之间没有关系:因伤致死比例和人群中牙医密度.
• D 图和 H 图中是 CC 和 MIC 都高,呈现近乎线性的相关性.
• E/F/G 这三个图都是低 CC 高 MIC.这是因为这些变量之间的关系是非线性的,例如在 E 图和 F 图中,都是非函数对应关系,比如可能是一对多的对应关系.

总的来说, MIC 这个统计量是基于互信息量的,可以用于发现变量之间的有意义的关系,而这些关系可能是那些简单的统计量,比如相关系数之类无法反应的.由于这个优势, MIC 也被称作是21世纪的相关性衡量变量“a correlation for the 21st century” (Speed 2011).