Task04回归模型的评估和超参数调优
1. 回归模型的评估
模型的评估包含三个指标:SSE(误差平方和)、R-square(决定系数)和Adjusted R-Square (校正决定系数)
1.1 SSE – 误差平方和
公式如下:

对同一个数据集,不同模型会有不同的SSE,SSE越小,说明模型的误差越小,准确率越高。
对不同的数据集,随着数据集的增加,误差也会增大,因此此时研究SSE没有意义。
1.2 R-square – 决定系数
决定系数是通过数据的变化来表征一个拟合的好坏。
公式如下:

分母是原始数据的离散程度,分子为预测数据和原始数据的误差平方和,二者相除可以消除原始数据离散程度的影响。
理论上R的取值范围(-∞,1],但在实际应用中的取值范围为[0 1] ------ 实际操作中通常会选择拟合较好的曲线计算R²,因此很少出现-∞。
R越接近1,表明方程的变量对y的解释能力越强,这个模型对数据拟合的也较好。
R越接近0,表明模型拟合的越差。
经验值:>0.4, 拟合效果好。
1.3 Adjusted R-Square – 校正决定系数
公式如下:
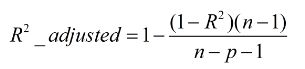
其中n为样本数量,p为特征数量。
优点:校正决定系数消除了样本数量和特征数量的影响。
2. 超参数调优
2.1 参数调优
模型参数是模型内部的配置变量,其值可以根据数据进行估计。一下是参数的一些特点:
参数在预测中用到,是从数据估计中获取的。
参数定义了可使用的模型,通常不由编程者手动设置。
参数通常被保存为学习模型的一部分,它是机器学习算法的关键,通常由过去的训练数据中总结得出 。
2.2 超参数调优
模型超参数是模型外部的配置,其值无法从数据中估计。
超参数通常用于帮助估计模型参数,通常由人工指定。
超参数通常可以使用启发式设置。
超参数经常被调整为给定的预测建模问题,取不同的超参数的值对于模型的性能有不同的影响。
3. 超参数的应用
3.1 网格搜索GridSearchCV()
网格搜索是从超参数空间中寻找最优的超参数,很像一个网格中找到一个最优的节点。
举例: =0.01,0.1,1.0 和 =0.01,0.1,1.0 , 组成一份排列组合,即:{[0.01,0.01],[0.01,0.1],[0.01,1],[0.1,0.01],[0.1,0.1],[0.1,1.0],[1,0.01],[1,0.1],[1,1]} ,然后针对每组超参数分别建立一个模型,然后选择测试误差最小的那组超参数。
3.2 随机搜索 RandomizedSearchCV()
随机搜索中的每个参数都是从可能的参数值的分布中采样的。
与网格搜索相比,随即搜索有以下优点:
(a). 可以独立于参数数量和可能的值来选择计算成本。
(b). 添加不影响性能的参数不会降低效率。
4. 代码实现过程
import numpy as np
import pandas as pd
from sklearn.svm import SVR # 引入SVR类
from sklearn.pipeline import make_pipeline # 引入管道简化学习流程
from sklearn.preprocessing import StandardScaler # 由于SVR基于距离计算,引入对数据进行标准化的类
from sklearn.model_selection import GridSearchCV # 引入网格搜索调优
from sklearn.model_selection import cross_val_score # 引入K折交叉验证
from sklearn import datasets
boston = datasets.load_boston() # 返回一个类似于字典的类
X = boston.data
y = boston.target
features = boston.feature_names
pipe_SVR = make_pipeline(StandardScaler(),
SVR())
score1 = cross_val_score(estimator=pipe_SVR,
X = X,
y = y,
scoring = 'r2',
cv = 10) # 10折交叉验证
print("CV accuracy: %.3f +/- %.3f" % ((np.mean(score1)),np.std(score1)))
CV accuracy: 0.187 +/- 0.649
# 网格搜索SVR调参:
from sklearn.pipeline import Pipeline
pipe_svr = Pipeline([("StandardScaler",StandardScaler()),
("svr",SVR())])
param_range = [0.0001,0.001,0.01,0.1,1.0,10.0,100.0,1000.0]
param_grid = [{"svr__C":param_range,"svr__kernel":["linear"]}, # 注意__是指两个下划线,一个下划线会报错的
{"svr__C":param_range,"svr__gamma":param_range,"svr__kernel":["rbf"]}]
gs = GridSearchCV(estimator=pipe_svr,
param_grid = param_grid,
scoring = 'r2',
cv = 10) # 10折交叉验证
gs = gs.fit(X,y)
print("网格搜索最优得分:",gs.best_score_)
print("网格搜索最优参数组合:\n",gs.best_params_)
网格搜索最优得分: 0.6096834373642706
网格搜索最优参数组合:
{‘svr__C’: 1000.0, ‘svr__gamma’: 0.001, ‘svr__kernel’: ‘rbf’}
# 随机搜索SVR调参:
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import uniform # 引入均匀分布设置参数
pipe_svr = Pipeline([("StandardScaler",StandardScaler()),
("svr",SVR())])
distributions = dict(svr__C=uniform(loc=1.0, scale=4), # 构建连续参数的分布
svr__kernel=["linear","rbf"], # 离散参数的集合
svr__gamma=uniform(loc=0, scale=4))
rs = RandomizedSearchCV(estimator=pipe_svr,
param_distributions = distributions,
scoring = 'r2',
cv = 10) # 10折交叉验证
rs = rs.fit(X,y)
print("随机搜索最优得分:",rs.best_score_)
print("随机搜索最优参数组合:\n",rs.best_params_)
随机搜索最优得分: 0.3053064654342476
随机搜索最优参数组合:
{‘svr__C’: 1.3018802059376666, ‘svr__gamma’: 2.936055000758253, ‘svr__kernel’: ‘linear’}