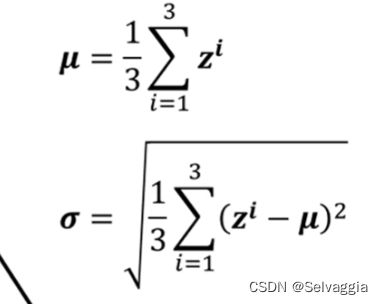loss&BN
still tips for learning
-
- classification and regression
- 关于softmax的引入和作用
- 分类问题损失函数 - MSE & Cross-entropy⭐
- Batch Normalization(BN)⭐
-
- 想法:直接改error surface的landscape,把山铲平
- feature normalization
- 那我们如何继续传播normalization的参数呢?
- 添加参数γ,β调整输出分布
- testing (又叫inference中),pytorch提供moving average
- 对batch normalization的研究结果
- 援引
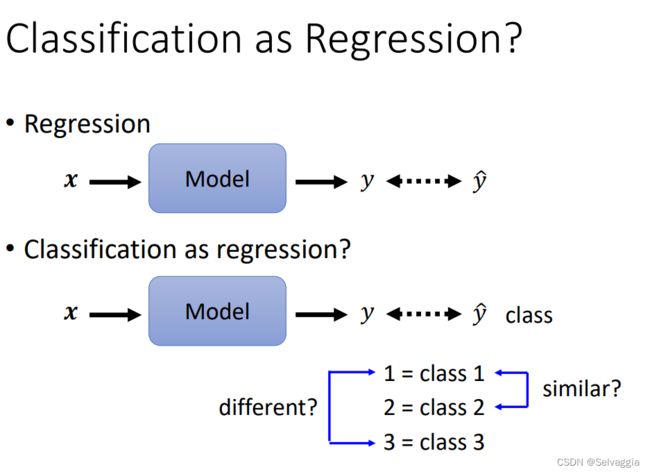
classification and regression
分类和回归做的事情都差不多,不同的是最后输出结果,分类输出的 y 是向量,不是数值,最后的 y’ 要把 y 经过一个softmax函数再输出,使 y’ 的值在0~1之间
之前分类宝可梦,讲到 把分类问题向回归问题靠拢,分类的输出应当如何表示?
把每一类当作一个数字,但是数字之间有关系,类别之间不一定和数字之间的关系保持一致比如大小,是否相邻
实际问题中,有可能真的存在这种类别间的相似关系。例如:用身高和体重预测学生的年级。一年级和二年级的身高和体重比较接近,但一年级和三年级的身高和体重比较不相似。
若将分类问题当做回归问题,正确的类别编码方式是:将类别表示为独热码one-hot vector。这种向量表示法,不会使类别间产生不存在的相似关系,神经网络需要输出的结果不再是一个数值,而是一个向量,向量的元素个数与类别个数相同。
关于softmax的引入和作用
从generative的model开始讲起,一路讲到logistic regression
因为softmax是从generative model的后验概率式子推出来的
softmax的输入往往被叫做 Logit
softmax的作用:除了normalize以外,还可以对最大值做强化,因为在做第一步的时候,对原始输出z取exponential会使大的值和小的值之间的差距被拉得更开,也就是强化大的值。
浅浅打一个问号????
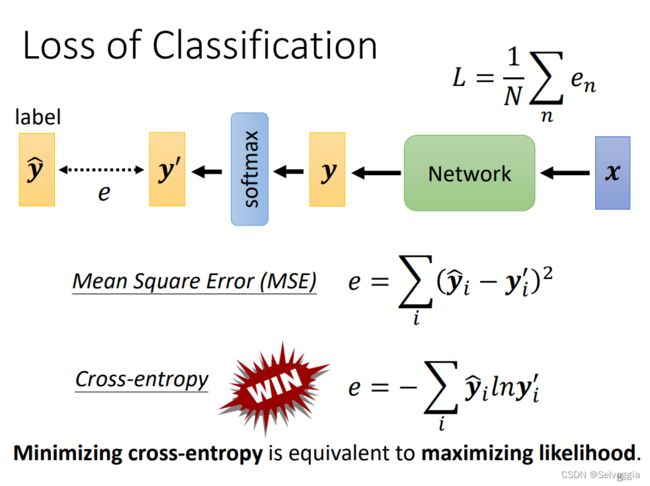
分类问题损失函数 - MSE & Cross-entropy⭐
cross-entropy,win!!! cross-entropy常用到 cross-entropy 和 softmax 在pytorch里面是绑在一起的
copy cross-entropy,里面自动内建了softmax,使用cross-entropy的时候,pytorch自动把softmax加在network的最后一层
why win?
explain1:交叉熵其实是用极大似然式子推出来的???
explain1:
从optimization的角度
1、数学证明 链接废了
2、举例说明
根据 label data可以知道最终的分类结果是y1
y3进行exp运算后非常小,可以忽略不记,看y1,y2
y1越大y2越小自然就是loss最小的情形啦,如右下角
左上角反之
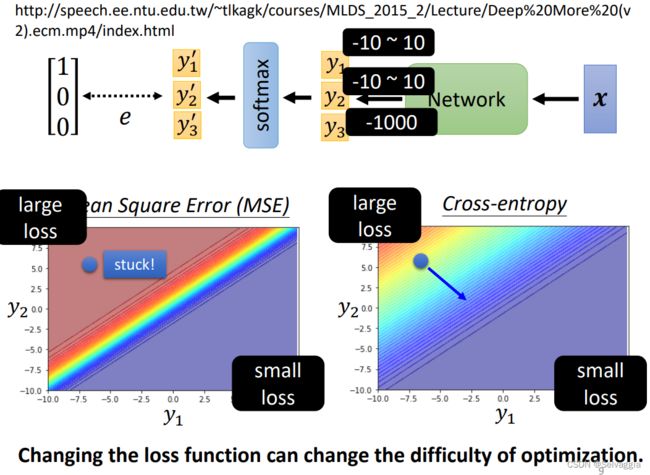
通过cross-entropy,左上角有斜率,有办法通过gradient往下走,
卡住了,在loss很大的地方很平坦,gradient非常小趋近于0,离目标又很远,很大可能性就train不下去
因为Cross-entropy的左上角比较陡峭,所以收敛更快更好,MSE左上角比较平缓,所以收敛较慢。
loss function的定义都能影响train的容易程度
Batch Normalization(BN)⭐
想法:直接改error surface的landscape,把山铲平
常用在 CNN、影像处理
直接改landscape,error surface 很崎岖的时候比较难train
把山铲平,让他容易train一点
when error surface is confessed,是个碗的形状,都不见得很好train
假设两个参数对loss的斜率差别非常大,在w1这个方向变化很小,在w2这个方向变化很大,坡度非常不一样,在固定的learning rate上很难得到好的结果
需要adapted Learning rate,如Adam,等进阶的optimization
或者一个更直接的想法:直接改landscape
两个参数对loss的斜率差别非常大,这种现象产生的根本原因是什么
在w1这个方向变化很小,可能输入很小,对L影响很小
w1改变一点,对L影响不大
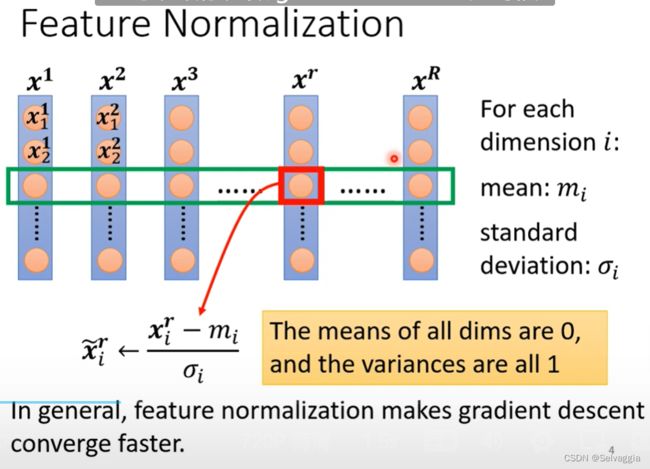
于是 制造出近似于"圆形"(各方向平滑)的 error surface,有很多办法,统一命名为Feature Normalization,下面是一种Feature Normalization。
让feature里面不同的dimension 有相同的数值范围,制造一个比较好的error surface
很多种方法,统称为feature normalization
feature normalization
这种操作其实叫做标准化,standardization,,除以的是标准差(Standard Deviation)
得到normalization以后的数值放回每一行相应的位置,这样的好处是
1、做完 normalize 以后,每个维度上面的数值就会平均是 0,然后它的 方差和就会是 1,所以这一排数值的分布就都会在0 00 上下
2、对每一个维度都做一样的 normalization,就会发现所有 feature 不同维度的数值都在 0 上下,那因为不同x
xx的取值范围接近,可能会制造出一个好的error surface,让loss收敛得更快一点,达到训练加速的效果。3、因为我们大多都采用Sigmoid
Function,它的图象是越远离0越不敏感,存在着一定的饱和区间,这样将数据都集中在0附近可以更快更新梯度。
假设 x ⃗ 1 \vec x^1 x1到 x ⃗ R \vec x^R xR是我们所有的训练资料 的 feature vector
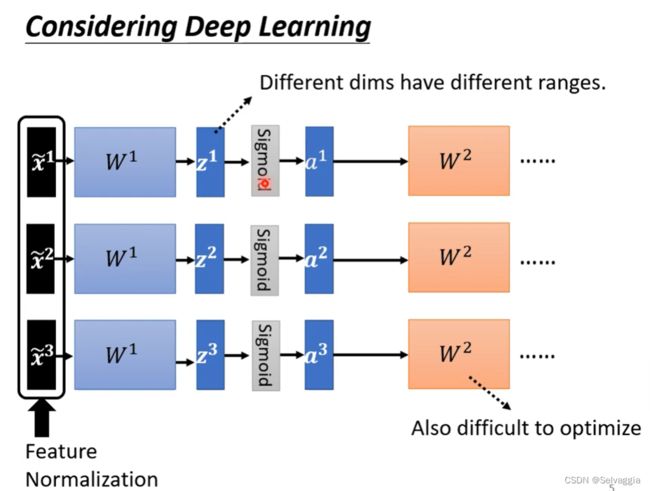
我们将 x ~ r \tilde{x}^r x~r 传到神经网络后,与 w ~ r \tilde{w}^r w~r相乘得到 Z ~ r \tilde{Z}^r Z~r ,虽然我们的
x ~ r \tilde{x}^r x~r 经过了Normalization,但 Z ~ r \tilde{Z}^r Z~r
还是再不同的区间,他们的分布仍然有很大的差异的化,我们再训练下一层的时候还是会遇到相同的困难,所以我们这边要对 Z ~ r \tilde{Z}^r Z~r
或者是 a ~ r \tilde{a}^r a~r 也进行一次Normalization的操作
在activation function之前还是之后做normalization呢,差别不大
但如果选择得是sigmoid function,推荐在activation function之前做feature normalization,因为sigmoid函数S形状嘛,在0附近斜率比较大,选择在 Z ~ r \tilde{Z}^r Z~r后面进行Normalization的操作,把所有的挪到0附近,gradient就比较大
那我们如何继续传播normalization的参数呢?
方法如下:那你就把 Z ~ r \tilde{Z}^r Z~r 想成是另外一种 feature ,我们这边有 Z 1 ~ r \tilde{Z1}^r Z1~r 、 Z 2 ~ r \tilde{Z2}^r Z2~r 、 Z 3 ~ r \tilde{Z3}^r Z3~r
,我们就把 Z 1 ~ r \tilde{Z1}^r Z1~r 、 Z 2 ~ r \tilde{Z2}^r Z2~r 、 Z 3 ~ r \tilde{Z3}^r Z3~r 拿出来,算一下它的 mean,
这边的 μ ~ \tilde{μ} μ~ 是一个 vector
(嗯?如果我没理解错的话,这里说 μ ~ \tilde{μ} μ~和 σ ~ \tilde{σ} σ~ 都是代表着vector是因为整体数据分成了若干个batch,每个batch对应一个μ和σ,但愿,没理解错★),
我们就把 Z 1 ~ r \tilde{Z1}^r Z1~r 、 Z 2 ~ r \tilde{Z2}^r Z2~r 、 Z 3 ~ r \tilde{Z3}^r Z3~r 这三个 vector 算他们的平均值得到 μ ~ \tilde{μ} μ~,再算他们的标准差得到 σ ~ \tilde{σ} σ~ , 它也代表了一个 vector,
然后
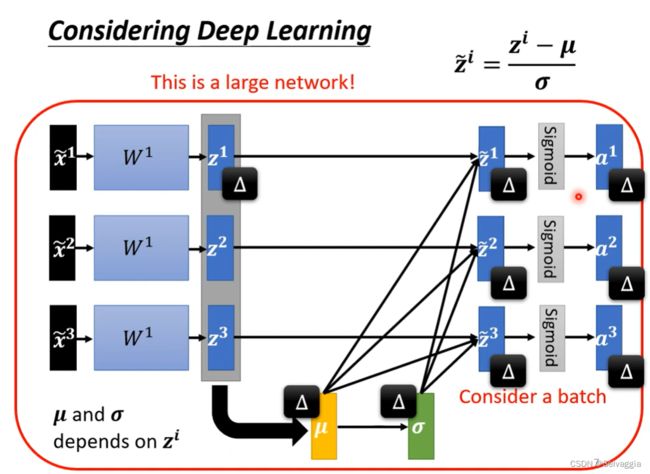
之前独立处理,现在变得彼此关联了
z 1 z^1 z1 改变,123都跟着改变

看来一定要有个够大的batch size,这个batch才足以表示整个copes的分布
添加参数γ,β调整输出分布
往往还有这样的设计
γ,β,是network的参数,另外再learn出来的
输出的平均值是0,也许会给network一些限制,带来一些负面影响, 于是设计γ,β来调整输出的分布

那为什么要加上β 跟 γ 呢,如果我们做 normalization 以后,那这边的z ,它的平均就一定是 0那也许,今天如果平均是 0 的话,就是给那 network一些限制,也许这个限制会带来什么负面的影响,所以我们把 β 跟 γ 加回去,后面network会自己调整 β 跟 γ的值。
但这不是和之前我们初衷相背离了嘛,我们之前就是想要他们保持在0附近并且range一样。其实没有,我们最开始的时候β ββ 的初始值里面全部都是0向量, γ γγ 就是里面全部都是1的向量,所以在训练开始阶段每一个dimension 的分布是比较接近的,但训练一段时间后已经找到一个比较好的 error surface,那再把γ 跟β 学习出其他的值慢慢地加进去。
testing (又叫inference中),pytorch提供moving average
不一定会一次性给定所有数据,或者是给够一个batch的数据,不能说等累计到一个batch再开始运算,于是pytorch提供了一个方法,moving average,大概就是在不完全具备一个batch的数据的时候就可以计算出一个 μ ~ \tilde{μ} μ~
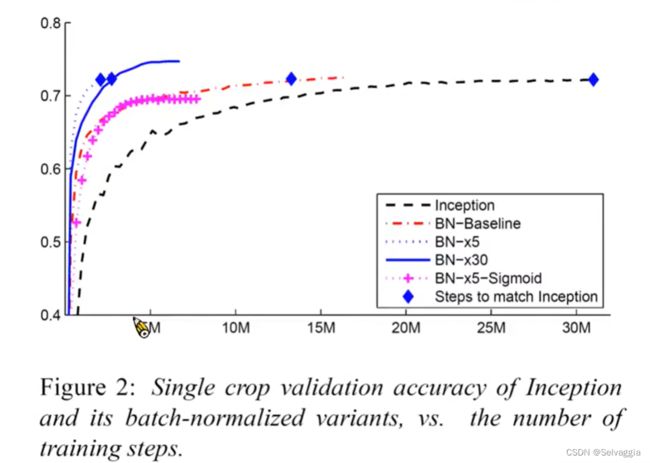
对batch normalization的研究结果
一般都会选择relu,sigmoid比较难train,但是加BN还是可以train起来
learning rate 变大30倍
援引
batch normalization这块的内容,笔记有照抄这位博主,笔记真难记!
BatchNorm和LayerNorm——通俗易懂的理解(还没学齐,据说解释的好,先码住!!!