Leetcode(155)——最小栈
Leetcode(232)——最小栈
题目
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
- MinStack() 初始化堆栈对象。
- void push(int val) 将元素val推入堆栈。
- void pop() 删除堆栈顶部的元素。
- int top() 获取堆栈顶部的元素。
- int getMin() 获取堆栈中的最小元素。
示例 1:
输入:
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]
输出:
[null,null,null,null,-3,null,0,-2]
解释:MinStack minStack = new MinStack(); minStack.push(-2); minStack.push(0); minStack.push(-3); minStack.getMin(); --> 返回 -3. minStack.pop(); minStack.top(); --> 返回 0. minStack.getMin(); --> 返回 -2.
提示:
- -231 <= val <= 231 - 1
- pop、top 和 getMin 操作总是在非空栈上调用
- push, pop, top, and getMin最多被调用 3*104 次
题解
关键是关键要解决的问题就是当有新的更小值的时候,之前的最小值该怎么办?
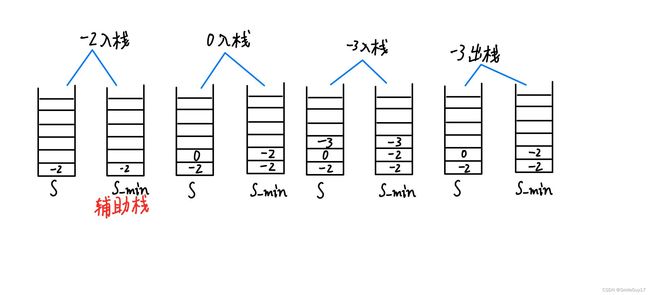
方法一:使用辅助栈保存最小值
思路
对于栈来说,如果一个元素 a 在入栈时,栈里有其它的元素 b, c, d,那么无论这个栈在之后经历了什么操作,只要 a 在栈中,b, c, d 就一定在栈中,因为在 a 被弹出之前,b, c, d 不会被弹出。
因此,在操作过程中的任意一个时刻,只要栈顶的元素是 a,那么我们就可以确定栈里面现在的元素一定是 a, b, c, d。那么,我们可以在每个元素 a 入栈时把当前栈的最小值 m 存储起来。在这之后无论何时,如果栈顶元素是 a,我们就可以直接返回存储的最小值 m。
按照上面的思路,我们只需要设计一个数据结构,使得每个元素 a 与其相应的最小值 m 时刻保持一一对应。因此我们可以使用一个辅助栈,与输入栈同步插入与删除,用于存储与每个元素作为栈顶的子栈的最小值。
- 当一个元素要入栈时,我们取当前辅助栈的栈顶存储的最小值,与当前元素比较得出最小值,将这个最小值插入辅助栈中;
- 当一个元素要出栈时,我们把辅助栈的栈顶元素也一并弹出;
- 在任意一个时刻,栈内元素的最小值就存储在辅助栈的栈顶元素中。
代码实现
class MinStack {
private:
stack<int> S; // 储存输入值
stack<int> S_min; // 储存最小值,同时push和pop
public:
MinStack() {
}
void push(int val) {
S.push(val);
// 如果新值小于之前的最小值,则将新值入S_min,否则将S_min的栈顶值再次入栈
// 且如果此时S_min为空栈,则直接将新值入栈
// 两个判断表示式的前后顺序不能改变,因为对空栈调用top会报错
// 而 || 运算符当前一个逻辑表达式为真时将不会执行下一个逻辑表达式
if(S_min.empty() || val < S_min.top())
S_min.push(val);
else S_min.push(S_min.top());
}
void pop() {
if(!S.empty()){
S.pop();
S_min.pop();
}
}
int top() {
return S.top();
}
int getMin() {
return S_min.top();
}
};
复杂度分析
时间复杂度:对于题目中的所有操作,时间复杂度均为 O ( 1 ) O(1) O(1)。因为栈的插入、删除与读取操作都是 O ( 1 ) O(1) O(1),而我们定义的每个操作最多调用栈操作两次
空间复杂度: O ( n ) O(n) O(n) ,其中 n n n 是操作总数。最坏情况下,我们会连续插入 n n n 个元素,此时两个栈占用的空间复杂度为 O ( n ) O(n) O(n)
方法二:在栈里保存之前的最小值(不使用辅助栈)
思路
1. 开始为了保证出栈操作的一致(即出栈时,若栈顶值等于当前最小值,则连续出栈两次,并将第二次出栈的值赋予保存当前最小值的变量),在当前栈为空栈时,需要把同一个数入栈两次;
2. 当有比当前最小值小的或相等的(为了出栈操作的统一)新值来的时候,我们只需要先把之前的最小值入栈,再将新值入栈并赋予保存最小值的变量即可;
3. 当出栈时,若栈顶值等于当前最小值,则连续出栈两次,并将第二次出栈的值赋予保存当前最小值的变量。
代码实现
class MinStack {
private:
stack<int> S;
int S_MIN;
public:
MinStack():S_MIN(0) {
}
void push(int val) {
if(S.empty()){
S.push(val);
S.push(val);
S_MIN = val;
}else if(val <= S_MIN){ // 将相等也视为新的最小值,为了操作的统一
S.push(S_MIN);
S.push(val);
S_MIN = val;
}else S.push(val);
}
void pop() {
if(top() == S_MIN){
S.pop();
S_MIN = S.top();
S.pop();
}else S.pop();
}
int top() {
return S.top();
}
int getMin() {
return S_MIN;
}
};
复杂度分析
时间复杂度:对于题目中的所有操作,时间复杂度均为 O ( 1 ) O(1) O(1)。因为栈的插入、删除与读取操作都是 O ( 1 ) O(1) O(1),而我们定义的每个操作最多调用栈操作两次
空间复杂度: O ( n ) O(n) O(n) ,其中 n n n 是操作总数。实际上在某些时候还是比方法一要少消耗很多空间。
方法三:在栈里保存差值(不使用辅助栈)
思路
同样是用一个 m i n min min 变量保存最小值。只不过栈里边我们不去保存原来的值,而是去存储入栈的值和最小值的差值。然后得到之前的最小值的话,我们就可以通过 min 值和栈顶元素得到,举个例子:
所以每次存入栈的是 原 值 − 当 前 最 小 值 原值 - 当前最小值 原值−当前最小值 的差值,所以出栈的获取的原值就是 栈 顶 值 + 当 前 最 小 值 栈顶值 + 当前最小值 栈顶值+当前最小值。
- 当原值大于等于当前最小值的时候,我们存入栈的差值肯定就是非负数。
- 当原值小于当前最小值的时候,我们存入栈的差值肯定就是负数,此时先用 m i n min min 保存新值,即新的当前最小值,再将计算后的差值入栈。
- 当出栈时,若栈顶元素是负数,那么原来入栈值就是 m i n min min 储存的值。若栈顶元素是非负数,之前 m i n min min 存储的最小值,我们可以通过用 m i n − 栈 顶 元 素 min -栈顶元素 min−栈顶元素 的差值获得。
该解法的一个缺点就是由于我们保存的是差值,所以可能造成溢出,所以可以采用了数据范围更大的 long 类型。
此外相对于解法二,解法三会省一些空间,最小值需要更新的时候,我们并没有将之前的最小值存起来,我们每次都是通过当前最小值和栈顶元素推出了之前的最小值。
代码实现
class MinStack {
long min;
stack<long> s;
public:
MinStack(){
}
void push(int x) {
if (s.empty()) {
min = x;
s.push(x - min);
} else {
s.push(x - min);
if (x < min){
min = x; // 更新最小值
}
}
}
void pop() {
if (s.empty())
return;
long tmp = s.top();
s.pop();
//弹出的是负值,要更新 min
if (tmp < 0) {
min = min - tmp;
}
}
int top() {
//负数的话,出栈的值保存在 min 中
if (s.top() < 0) {
return min;
//出栈元素加上最小值即可
} else {
return s.top() + min;
}
}
int getMin() {
return min;
}
};
复杂度分析
时间复杂度:对于题目中的所有操作,时间复杂度均为 O ( 1 ) O(1) O(1)。因为栈的插入、删除与读取操作都是 O ( 1 ) O(1) O(1),而我们定义的每个操作最多调用栈操作两次
空间复杂度: O ( n ) O(n) O(n) ,其中 n n n 是操作总数。实际上还是比方法二要少消耗一些空间。