2012年建模A题 葡萄酒的评价

A题 葡萄酒的评价

2012数模国赛A题下载链接：http://www.mcm.edu.cn/problem/2012/2012.html

解题思路

符号说明

先附上我的摘要

第一问

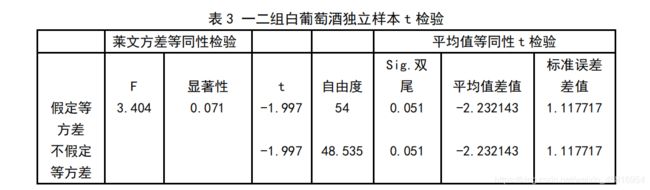
第一问分析两组评酒员的评价结果有无显著性差异，哪一组结果更可信就是对两组评酒员的评分的进行t检验并进行信度检验。
t检验的前提：

• 单组观测变量为连续变量；
• 观测值相互独立；
• 单组连续变量无明显异常值；
• 单组连续变量近似或服从正态分布。

若不满足上述条件则无法进行t检验，可以用秩和检验来做。
秩和检验的优缺点

秩和检验的优点是

• 不受总体分布限制，适用面广；
• 适用于等级资料及两端无确定值的资料；
• 易于理解，易于计算。缺点是符合参数检验的资料，用秩和检验，则不能充分利用信息，检验功效低。

应用中的注意事项：

• 注意应用条件；
• 编秩时相同值要取平均秩次；
• 相同秩次较多时，统计量要校正。

要进行t检验首先就要进行评分数据的正态检验。
常用的正态检验方法如下：

• 频率直方图
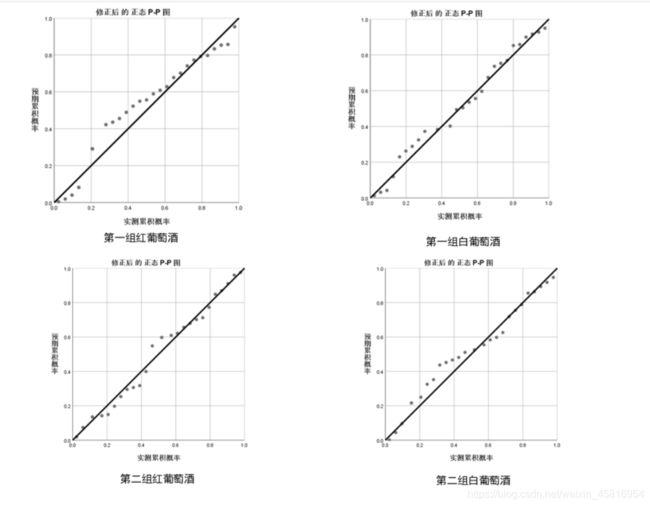
• P-P图
• Q-Q图
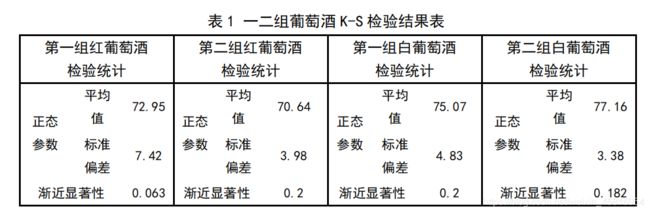
• K-S 检验
• 描述法(偏度和峰度系数检验)

这些检验都可用spss轻易的实现，具体的实现教程可以见博客的内容。

我们分别采用了P-P图和K-S 检验方法通过比较检测显著性水平 P 值，P 均大于 0.05，说明与正态性没有显著差
异，即葡萄酒的评分成正态性分布。

数据通过正态检验后就可以进行t检验了，结果如下：

得到两组数据没有显著性差异之后我们还要进行信度分析，得到那组评分更可信。

针对可信度评价，采用 Kendall’s W 一致性检验和 Cronbach’s
α一致性检验得出结论：第一组评酒员的评分结果更加可信。

得到的结果分别如下所示：

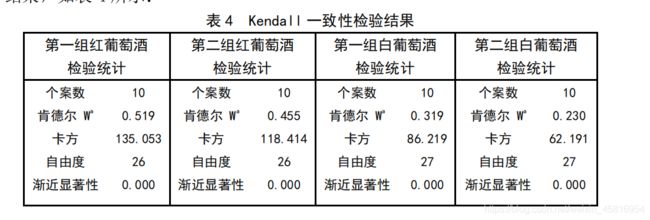
a) 第一组对红葡萄酒评价的 Kendall 系数为 0.519；第二组对红葡萄酒评价
的 Kendall 系数为 0.455。因此，在红葡萄酒的评价中，第一组评酒员的一致性
更高。
b) 第一组对白葡萄酒评价的 Kendall 系数为 0.319；第二组对白葡萄酒评价
的 Kendall 系数为 0.023。因此，在红葡萄酒的评价中，第一组评酒员的一致性
更高。

第二问

问题 2 要求根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级。但该问题中并没有给分级的标准和具体的分级数，所以该问题属于数据建模中的聚类问题。这样我们就可以利用一些聚类方法来求解该问题了。在众多聚类方法中，K-means 方法算法适应性比较强的方法，所以不妨先用 K-means 方法对所研究的数据进行聚类，然后还可以尝试用层次聚类、模糊聚类等方法, 以便于结果的比较和最佳聚类方法的选择。

下面我们就要来分析该对谁聚类，也就是说要来确定聚类的研究对象。问题中已明确规定根据酿酒葡萄的理化指标和葡萄酒的质量来实现对酿酒葡萄的分级。对葡萄酒的理化指标数据分析发现，理化指标比较多，用哪些指标是进行分级效果很难评判。但用葡萄酒质量数据来进行分级，既有直观的现实意义，操作性也比较可行，为此，可以先根据葡萄酒的质量来进行酿酒葡萄的分级。由第一问，可知，虽然第二组品酒师的数据更稳定，但两组品酒师的结果并没有显著差异，所以，应该以两组品酒师的平均值作为酒样的质量数据。

当根据葡萄酒的质量对酿酒葡萄进行分级后，然后就可以研究如何利用酿酒葡萄的理化指标来分级。这里面，由于理化指标的差异就是数值上的差异，而求解这类问题的一个典型的方法就是 PCA 方法，所以可以用 PCA 方法来实现对理化指标的降维，然后同样可以用上述的聚类方法来实现聚类。

%% 用聚类法确定葡萄酒分级
clc, clear all, close all
%% 需要聚类的数据
% 红葡萄酒质量评分数据
% A=[62.625	80.125	80.75	68.875	73.375	72.125	71.5	71.75	80.875	...
%     74	68.875	53.75	75.375	73.875	57.625	75	78.5	60	79.125	79	76.875...
%     76.375	85.375	77.75	68.875	74.625	72.75
% ]; 
% 白葡萄酒质量评分数据
A=[83	75.5	78.375	80.125	72.375	69.375	78.125	71.875	73.625	76.25...
    73.625	64.25	66.75	73.5	73.625	75	80.25	75.125	72	78.625	78.375...
    71.5	75.75	73.875	77.25	81.75	66.125	82.125
];
%% 用k-Means聚类法确定最佳的聚类数
X=A';
numC=7;
for i=1:numC
    kidx = kmeans(X,i);
    silh = silhouette(X,kidx); %计算轮廓值
    silh_m(i) = mean(silh);    %计算平均轮廓值
end

figure
plot(1:numC,silh_m,'ko-', 'linewidth',2)
set(gca,'linewidth',2);
xlabel('类别数')
ylabel('平均轮廓值')
title(' 不同类别对应的平均轮廓值')

% 绘制2至5类时的轮廓值分布图
 figure
 set(gca,'linewidth',2);
for i=2:5
    kidx = kmeans(X,i);
    subplot(2,2,i-1);
    [~,h] = silhouette(X,kidx);
    set(gca,'linewidth',2);
    title([num2str(i), '类时的轮廓值 ' ])
    snapnow
    xlabel('轮廓值');
    ylabel('类别数');
end

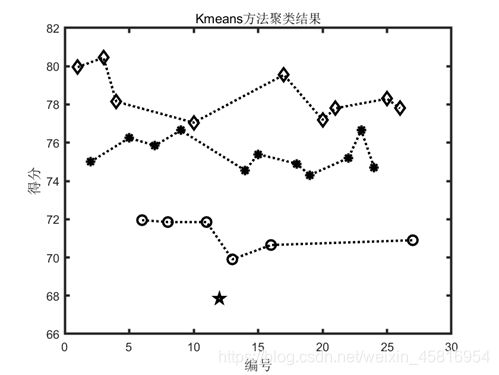
%% K-means聚类过程，并将结果显示出来
[idx,ctr]=kmeans(A',3); % 用K-means法聚类
% 提取同一类别的样品号
c1=find(idx==1); c2=find(idx==2); 
c3=find(idx==3); %c4=find(idx==4); 
figure
F1 = plot(find(idx==1), A(idx==1),'k:*', ...
     find(idx==2), A(idx==2),'k:o', ...
     find(idx==3), A(idx==3),'k:p');
set(gca,'linewidth',2);
set(F1,'linewidth',2, 'MarkerSize',8);
xlabel('编号','fontsize',12);
ylabel('得分','fontsize',12);
title('Kmeans方法聚类结果')
disp('聚类结果：');
disp(['第1类:' ,'中心点：',num2str(ctr(1)),'  ','该类样品编号：', num2str(c1')]);
disp(['第2类:' ,'中心点：',num2str(ctr(2)),'  ','该类样品编号：', num2str(c2')]);
disp(['第3类:' ,'中心点：',num2str(ctr(3)),'  ','该类样品编号：', num2str(c3')]);

c1_mean = mean(A(c1));
c2_mean = mean(A(c2));
c3_mean = mean(A(c3));

第3问

问题三要求分析酿酒葡萄与葡萄酒的理化指标之间的联系。因此，考虑建立模型以描述葡萄酒理的单个化指标与酿酒葡萄的多个理化指标之间的联系，通过模型分析酿酒葡萄的理化指标对葡萄酒的理化指标的影响。
根据附件二可知酿酒葡萄的理化指标数量较多，考虑到不同的理化指标对葡萄酒的理化指标的影响不同，可以构造相关系数矩阵对双方的理化指标进行关联性分析，并选取其中关联性较高的进行研究；然后考虑到酿酒葡萄的理化指标对葡萄酒的理化指标的综合影响情况，运用逐步回归分析得到相应的回归方程，然后再对其中指标进行分析。

得到的回归方程（部分）如下所示：

clc;
clear; B=xlsread('white.xlsx');
[m1,n1]=size(B);
 X=['y','='];
 for j=1:n1
 if ~isnan(B(1,j))
 if(B(1,j)<0)
 X=[X,[num2str(B(1,j)),'x',num2str(j)]];
 else
 X=[X,['+',num2str(B(1,j)),'x',num2str(j)]];
 end
 end
 end
 disp(X);
clc;
clear;
zb=xlsread('指标-红.xlsx');
score=xlsread('score.xlsx');
score=zscore(score);
score=score';
stepwise(zb,score,[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20
,21,22,23,24,25,26,27,28,29,30,31]);

第4问

问题四中，需要我们通过酿酒葡萄和葡萄酒的理化指标，得到对葡萄酒的质量的评价，并论证是否可行。因此，首先考虑在问题三的基础上，酿酒葡萄的理化指标通过影响葡萄酒的理化指标间接影响葡萄酒的质量。而葡萄酒的理化性质对葡萄酒质量的影响更为直接。因此我们考虑分析葡萄酒的理化指标对葡萄酒质量的影响，进而利用葡萄理化指标与葡萄酒理化指标之间高度的相关性来分析葡萄的理化指标对葡萄酒质量的影响。
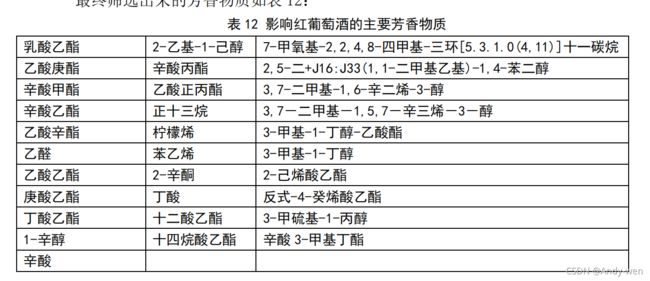
同时，查阅资料发现葡萄中的芳香物质对所酿出的葡萄酒的气味口感等方面会有较大影响，因此可以筛选出重要的芳香物质，与葡萄酒质量建立联系。

对芳香物质的筛选结果如下所示

白葡萄酒同理可得。

clear;clc;
% score = xlsread('../附件 1 整理.xls','红 1','B2:E28');
% zhibiao = xlsread('../附件 3-芳香物质.xls','红酒','B2:BV28');
score = xlsread('../附件 1 整理.xls','白 1','B2:E29');
zhibiao = xlsread('../附件 3-芳香物质.xls','白酒','B2:BV29');
load('name.mat');
score = zscore(score);
zhibiao = zscore(zhibiao);
res = [];
for i=1:73
 for j =1: 4
 t = corrcoef(score(:,j),zhibiao(:,i));
 res(i,j) = t(1,2);
 end
end
index = [];
for i=1:73
 if (res(i,2)>0 && res(i,3)>0)
 index = [index;i];
 end
end
name1 = name(index);