第四章 贪心算法 复习总结
一、贪心算法的两个基本性质
1.最优子结构
最优子结构:当前问题的最优解,一定包含了局部子问题的最优解。也就是问题也可以使用动态规划进行求解。贪心算法也要求问题具有最优子结构性质。
2.贪心选择性
贪心选择性:要求解当前问题,可以只考虑当前状态进行贪心选择,而不考虑得到当前的之前状态和贪心选择后的子问题状态。贪心选择后,问题规模缩小,而整体问题的最优解一定包含了刚刚的贪心选择和子问题的最优解。
3.补充说明
需要说明的是:考虑整体最优解时,若包含当前贪心选择,则满足贪心选择性。若不包含当前的贪心选择,可以进行剪切替换,将当前的贪心选择放入整体最优解中,并替换出一个其他解,此时若整体最优解仍然成立,则同样也满足贪心选择性。
二、贪心算法与其他算法的对比
从整体来看,贪心算法实现过程是由整体到局部的过程。即考虑当前整体问题,进行贪心选择,将问题转变为规模更小的子问题,依次迭代求解。
而动态规划求解方式与之恰好相反:考虑规模最小的子问题,解决子问题并保存到数组中,逐步扩大问题规模,对于重复的子问题可以不需要再次求解,而实现自底向上的求解。
三、贪心算法的局限性
由于每次选择都只考虑的当前问题状态而给出贪心选择,所以在求解过程中可能给出的最终结果并非整体问题的最优解,而只是近似最优解。另外根据不同的问题,贪心选择的策略也会有所不同,根据不同的选择策略,最终计算出的解也可能会各不相同。
-
不能保证求得的最后解是最佳的;
-
不能用来求最大或最小解问题;
-
只能求满足某些约束条件的可行解的范围
四、贪心算法的应用举例
1.区间覆盖问题
问题描述:
设x1,x2,… ,xn是实直线上的n个点。用固定长度的闭区间覆盖这n个点,至少需要多少个这样的固定长度闭区间?设计求解此问题的有效算法。对于给定的实直线上的n个点和闭区间的长度k,编程计算覆盖点集的最少区间数。
输入格式:
输入数据的第一行有2个正整数n和k,表示有n个点,且固定长度闭区间的长度为k。接下来的1行中,有n个整数,表示n个点在实直线上的坐标(可能相同)。
输出格式:
将编程计算出的最少区间数输出。
输入样例:
7 3
1 2 3 4 5 -2 6
输出样例:
3
分析:
区间覆盖问题的贪心选择是:先将需要覆盖的所有点从小到大排序,以最左端点为起始点,向右进行覆盖一个区间,然后将已在区间的点从集合中删除,更新下个子问题的最左端点并继续进行贪心选择。每次选择时都保证最左端的左侧没有区间长度被浪费,同时保证所有区间互相之间没有重叠。进行选择的过程中记录每个点被覆盖的区间编号记录到b数组并输出。
#include
#include
#include
using namespace std;
double a[1000];
int b[1000];
int cnt=1;
void solve(int n,int k){
sort(a,a+n);
double start=a[0];
for(int i=0;i>n>>k;
for(int i=0;i>a[i];
}
if(n){
solve(n,k);
cout< 运行结果:
2.Huffman编码问题
问题描述:
哈夫曼编码是广泛地用于数据文件压缩的十分有效的编码方法。其压缩率通常在20%~90%之间。哈夫曼编码算法用字符在文件中出现的频率表来建立一个用0,1串表示各字符的最优表示方式。一个包含100,000个字符的文件,各字符出现频率不同,如下表所示:

有多种方式表示文件中的信息,若用0,1码表示字符的方法,即每个字符用唯一的一个0,1串表示。若采用定长编码表示,则需要3位表示一个字符,整个文件编码需要300,000位;若采用变长编码表示,给频率高的字符较短的编码;频率低的字符较长的编码,达到整体编码减少的目的,则整个文件编码需要(45×1+13×3+12×3+16×3+9×4+5×4)×1000=224,000位,由此可见,变长码比定长码方案好,总码长减小约25%。
输入格式:
输入数据的第一行有1个正整数n,表示有n个需要编码的字符。接下来的n行中,每行有一个字符和一个整数,表示要编码的字符和此字符在文本中出现的频率。
输出格式:
输出每个字符的边长Huffman编码。
输入样例:
6
a 45
b 13
c 12
d 16
e 9
f 5
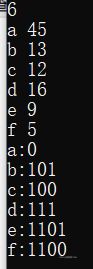
输出样例:
a:0
b:101
c:100
d:111
e:1101
f:1100
分析:
Huffman编码的算法思路是:读入每个要编码的字符和他们出现的频率,将他们保存在tree结构体中,并加入优先队列。利用优先队列数据结构,贪心选择每次取出出现频率最小的两个节点,将他们合并为,并将合并后的节点插入队列。出口为队列中仅剩一个元素,那么这就是整个Huffman树的根基点。利用solve函数遍历访问此树,将每个节点的编码保存在map中,利用print函数输出每个字符的Huffman编码。
#include
#include
#include
#include
#include 运行结果:
3.单源最短路径问题(Dijkstra算法)
问题描述:
如下图,给出一个有向图,请输出从某一点出发到所有点的最短路径长度。
![]()
![]()
输入格式:
第一行包含三个整数 n,m,s 分别表示点的个数、有向边的个数、出发点的编号。
接下来 m 行每行包含三个整数 u,v,w 表示一条 u→v 的,长度为 w 的边。
输出格式:
输出一行 n个整数,第 i个表示 s 到第 i 个点的最短路径
输入样例:
5 7 1
1 4 30
1 5 100
1 2 10
2 3 50
3 5 10
4 3 20
4 5 60
输出样例:
0 10 50 30 60
分析:
单源最短路径问题的思路是:读入所有结点信息,保存在数组中,并建立对应的djs结构体插入优先队列。算法先将开始节点标记已到达,循环贪心选择每次从优先队列中取出未到达过的,且距离已到达点的集合中最近的一个点,将该点标记为已经到达,并且进行松弛,如果到达节点距离更近则更新。最后打印dist数组即为最终结果。
#include
#include
#define MAX 99999
using namespace std;
struct djs{
int name;//以点name为终点
int value;//记录路途花费
bool operator<(const djs &d)const{
return value>d.value;
}
};
priority_queue q;
int a[1000][1000];
int dist[1000];
int b[1000];
void init(int n){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
a[i][j]=MAX;
}
dist[i]=MAX;
djs d;
d.name=i;
d.value=dist[i];
q.push(d);//初始条件入队
}
}
int findmin(int n){
djs d=q.top();
q.pop();
while(b[d.name]){//找到未确定的点
d=q.top();
q.pop();
}
b[d.name]=1;
return d.name;
// int min=MAX;
// int index=0;
// for(int i=1;i<=n;i++){
// if(dist[i]>n>>m;
init(n);
int start;//开始节点
cin>>start;
for(int i=0;i>x>>y>>L;
a[x][y]=L;
}
dist[start]=0;
for(int i=0;i 运行结果:
五、贪心算法总结
贪心算法在实现上相比动态规划而言,简单不少,但是在应用贪心策略之前,一定要对问题进行判断,看是否满足应用贪心算法的条件,即是否满足最优子结构和贪心选择性两个基本性质。
贪心算法满足最优子结构性质,也意味着此问题也可以运用动态规划求解,具体应该如何求解由我们自己来选择。
由于贪心算法并不一定得到整体的最优解,只能保证得到近似最优解,所以对于问题求解的最后要对贪心解进行简单的分析判断。
对于贪心算法应用过程中,对于不同的贪心选择方案,最终结果可能不同,这就需要读者熟练掌握各类贪心问题对应的贪心选择策略,才能找到更加近似于最优解的贪心解。