机器人正运动学(8)—— DH坐标系建立技巧
目录
-
- 1. 引言
- 2. 建立DH坐标系的技巧
-
- 2.1 理清关节和连杆
- 2.2 画 z 轴
- 2.3 确定 x 轴
-
- 2.3.1 x轴方向
- 2.3.2 x轴起始点(坐标系原点)
- 2.4 小结
- 3. 总结
1. 引言
关于DH参数上一篇文章介绍了基本概念和物理意义,但是还有一些内容没有提到。这篇文章主要介绍DH坐标系建立的一些技巧。
2. 建立DH坐标系的技巧
DH参数本身并不复杂,但是最初我在应用DH参数对机器人建立坐标系时的感受就一个字,乱。乱的原因是比较多的,罗列一下有这么几个点:
- 在机器人上不太容易一一区分出各个连杆,而且连杆编号也容易乱
- 无法确定一段距离是连杆偏距 d d d 还是连杆长度 a a a
- 难以确定坐标系的 x x x 轴方向
- 建立完坐标系后发现通过DH变换无法使坐标系重合
那么建立DH坐标系有没有什么技巧呢?还真有,而且很有效。下面我们来介绍一下如何快速建立机器人的DH坐标系。
2.1 理清关节和连杆
第一步至关重要,你得首先搞清楚哪个是关节1,哪个是连杆1,与连杆1固连的坐标系1原点在哪里等等。还是想再次强调DH坐标系是建立在连杆的传动轴也就是远离基座的那个轴。因此对于串联机器人来说关节,连杆,坐标系按照距离基座由近到远排列应该是这样的:首先肯定是关节1,其次是安装在关节1上的连杆1,然后是与连杆1固连的坐标系1,之后是关节2。请注意连杆1的坐标系 z 轴轴线实际是连杆2的驱动轴。
我们以一个六轴机器人建立DH坐标系为例,为了方便看清楚各个连杆,我把每个连杆涂成了不同的颜色,如下图所示。

想象一下如果没有给各个连杆涂上颜色,你还能一下子看出所有的连杆吗?你还能一下子区分出连杆1的坐标系应该建立在哪里吗?
2.2 画 z 轴
第二步我们要确定各个连杆坐标系的 z 轴,这一步实际上是比较容易的,因为按照规则 z 轴应该是和关节轴同向的。所以这里你唯一需要搞清楚的是这些 z 轴分别是固连在哪个连杆上。由于DH参数是在传动轴上建立坐标系的(请原谅我已经无数次在强调这个问题,因为我曾经无数次掉进这个坑里),所以 z 轴肯定是建立在连杆远离基座一侧的那个轴上的。
以下我们把与连杆固连的坐标系涂成与连杆相近的颜色。请先在自己的脑海中构思一下,看看你建立的 z 轴与下面的图是一致的吗。
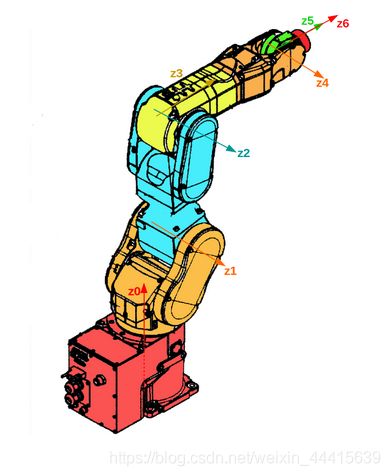
2.3 确定 x 轴
第三步我们需要确定 x 轴,这一步是最关键也是比较困难的一部分。在这里需要确定的有两点,第一点你需要确定 x 轴的方向第二点你得搞清楚坐标系的原点在哪里,也就是需要确定 x 轴的起始点。
2.3.1 x轴方向
我们先解决第一点。DH坐标系的 x 轴是连杆的驱动轴和传动轴的公垂线。所以 x 轴的方向相对而言是比较容易获得的。我们知道两个不平行的向量的叉乘(外积)就是两个向量的公垂线了。所以我们定义: x i = z i − 1 × z i x_{i}=z_{i-1}\times z_{i} xi=zi−1×zi
这里简单介绍一下公垂线方向的确定:叉乘遵守右手定则,如下图所示,当右手的四指从 a ⃗ \vec{a} a 以不超过180度的转角转向 b ⃗ \vec{b} b 时,竖起的大拇指指向是 c ⃗ \vec{c} c 的方向,即公垂线的方向。

这样你就可以确定连杆坐标系 x 轴的轴线了。最终 x 轴的指向你可以统一让它们指向传动轴。当驱动轴和传动轴平行时也很简单,你只需要画一条与两个轴都垂直且相交的向量,并且这个向量指向传动轴就可以了。
2.3.2 x轴起始点(坐标系原点)
接下来解决第二点。怎么确定坐标系 x 轴的起点(其实就是坐标系原点)。提前说明一下,当连杆的驱动轴和传动轴是异面直线时这个问题是不存在的,因为异面直线的公垂线有且仅有一条,这个时候原点已经随着 x 轴的确定一起确定下来了(就是 x 轴和 z 轴的交点)。
除了异面直线之外,驱动轴和传动轴还有两种关系,一个是平行关系,另一个是相交关系。这两种关系下驱动轴和传动轴的公垂线有无数条。在这个时候要如何确定坐标系的原点呢?
按照DH的规则,两个 z 轴之间公垂线长度代表的是抽象的连杆长度,两个 x 轴的公垂线长度代表的相邻两个连杆之间的偏距。你在确定坐标系原点时就需要考虑这些参数物理含义了。由于 z 轴已经全部确定了, x 轴的方向也确定了,所以这个时候各个连杆的长度也就是DH参数中的 a 已经确定了。那么我们在选择 x 轴的起点时必须要保证经过上一个连杆 i-1 的坐标系绕 z i − 1 z_{i-1} zi−1 轴旋转和沿 z i − 1 z_{i-1} zi−1 轴平移后能让 x i − 1 x_{i-1} xi−1 和 x i x_{i} xi 重合。当你发现经过这样的变换不能让 x i − 1 x_{i-1} xi−1 和 x i x_{i} xi 重合时说明你的连杆 i 坐标系选择的原点有问题。
上面这么说还是太晦涩了,我们举个例子。上面的六轴机器人连杆2的驱动轴和传动轴平行,连杆3的驱动轴和传动轴相交,我们就以这两个连杆为例来说明坐标系原点的确定过程。
在这之前我们还是先把基坐标系和连杆1坐标系确定下来,通常基座的 x 轴指向机器人的正前方。因此基坐标系很容易就确定下来了。连杆1的驱动轴和传动轴是异面直线,因此连杆1的坐标系 x 轴也可以轻松地根据前面提到的叉乘公式确定。这样基座和连杆1的坐标系就确定完了,如下图所示。

接下来的连杆2和连杆3就比较特殊了。当你试图找到 z 1 z_{1} z1 和 z 2 z_{2} z2 的公垂线时你发现又无数条。对于这种平行的连杆怎么确定其 x 轴呢?其实很简单,你的连杆 1 坐标系不是已经确定好了嘛,只需要过这个坐标系原点作垂线与 z 2 z_{2} z2 相交就可以了。这其实是最简单的连杆,不要把这个问题想复杂了就好。如果不相信,你可以按照前面说的规则检验一下。连杆 2 的坐标系确定之后如下图所示。

接下来就是连杆3了,你会发现连杆3的驱动轴和传动轴是相交的。连杆3的 x 3 x_{3} x3 方向是容易确定的,因为只要驱动轴和传动轴不平行我们就可以利用叉乘公式确定确定 x 轴的方向。但是同样的,这样的 x 轴有无数个,要怎么选择呢?你可以试一下选 z 2 z_{2} z2 和 z 3 z_{3} z3 的交点。先告诉各位这是对的。其实可以多找几个点,你会发现无论原点选在除这个点之外的任何地方,你要么需要在某个中间步骤向y轴平移,要么就是最终你需要在 z 轴方向再平移一段。这样我们就确定了连杆3的坐标系,如下图所示。观察后你会发现两个坐标系的原点重合,这说明连杆长度和连杆偏距都为0,这就是此类连杆的一个特点。
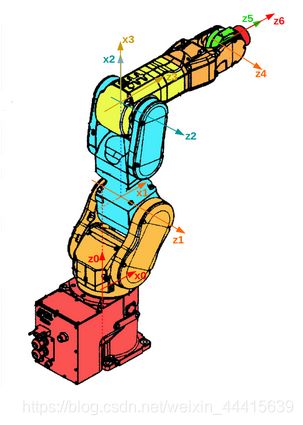
后面的连杆4也是类似的,驱动轴和传动轴相交,注意图里面的 z 3 z_{3} z3 很不明显,不要把 z 2 z_{2} z2 当成 z 3 z_{3} z3 哦。叉乘后发现 x 4 x_{4} x4 向下,原点当然也是在 z 3 z_{3} z3 和 z 4 z_{4} z4 的交点。后面的连杆也都大同小异。这里我就不一一介绍了。
最后的六轴机器人DH坐标系建立完成后如下图所示。
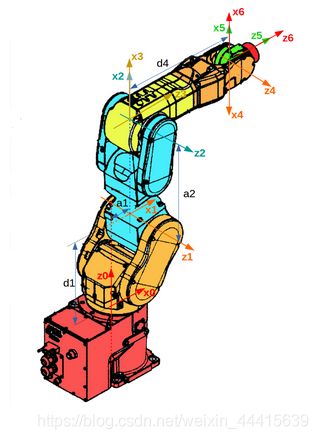
最后我们写出这个机器人的DH参数表如下表所示。
| 连杆编号 | θ \theta θ | d d d | a a a | α \alpha α | offset |
|---|---|---|---|---|---|
| 1 | θ 1 \theta_{1} θ1 | d 1 d_{1} d1 | a 1 a_{1} a1 | 9 0 ∘ 90^{\circ } 90∘ | 0 |
| 2 | θ 2 \theta_{2} θ2 | 0 | a 2 a_{2} a2 | 0 | 9 0 ∘ 90^{\circ } 90∘ |
| 3 | θ 3 \theta_{3} θ3 | 0 | 0 | 9 0 ∘ 90^{\circ } 90∘ | 0 |
| 4 | θ 4 \theta_{4} θ4 | d 4 d_{4} d4 | 0 | 9 0 ∘ 90^{\circ } 90∘ | 18 0 ∘ 180^{\circ } 180∘ |
| 5 | θ 5 \theta_{5} θ5 | 0 | 0 | 9 0 ∘ 90^{\circ } 90∘ | 18 0 ∘ 180^{\circ } 180∘ |
| 6 | θ 6 \theta_{6} θ6 | 0 | 0 | 0 | 0 |
关于offset项是叠加在 θ \theta θ 上面的偏置量,你可以理解为机器人处于零位时,驱动轴和传动轴依然存在夹角。
2.4 小结
前面感觉啰嗦了很多,不知道有没有说清楚,这里简单总结一下:当连杆驱动轴和传动轴是异面直线,公垂线(唯一)就是连杆的 x 轴;当连杆的驱动轴和传动轴平行时,找到上一个连杆的坐标系原点,向当前连杆的 z 轴作垂线,垂足就是当前连杆原点,垂线就是 x 轴;当连杆的驱动轴和传动轴相交时,交点就是连杆坐标系原点,驱动轴和传动轴的叉乘就是 x 轴方向。
这一块还是需要各位仔细去品味的,相信你经过不断的思考和尝试,一定可以变得通透。写这篇博客挺费力的,作图时间很长,但是我真的在这个过程里受益匪浅,对DH坐标系的理解也更进了一步。如果你一下子还不能完全理解,千万别着急,可以先放着,过几天再看,相信一定会有新的收获。
3. 总结
这篇文章我们主要介绍了DH坐标系建立的一些技巧,下一篇文章会介绍修改DH参数以及和标准DH参数之间的差别。由于个人能力有限,所述内容难免存在疏漏,欢迎指出,欢迎讨论。
下一篇:机器人正运动学(9)—— 修改DH参数
————————————————
版权声明:本文为CSDN博主「hitgavin」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/hitgavin/article/details/104766458