线性神经网络
目录
线性神经网络概述
Delta学习规则
解决异或问题
线性神经网络概述
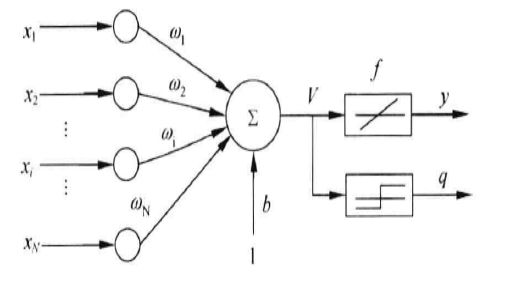
线性神经网络在结构上与感知器非常相似,只是激活函数不同,是在模型训练时把原来的sign函数改成了purelin函数:y=x。感知器的输出只能是两个数-1和1,但是线性神经网络的输出可以取任何值,其传输函数是线性函数。
下图就是一个线性神经网络模型,如图:x1,x2,xN为输入节点,w1,w2,wN为权向量,b为偏置因子,f为激活函数(purelin函数),神经网络的输出不仅产生二值输出以外(q),还可以产生模拟输出(y)。
Delta学习规则
该学习规则是一种利用梯度下降法的一般性的学习规则
二次代价函数:E = 1/2(t-y)^2 = 1/2[t-f(WX)]^2;
误差E是权向量W的函数,欲使误差E最小,W应与误差的负梯度成正比;即ΔW = -η▽E。
梯度就是求导,即求导可得▽E = -X.T(t-y)f’(WX)
可以推出权值调整的公式ΔW=ηX.T(t-y)f’(WX)
梯度下降法的问题:
- 学习率难以选择,太大会产生震荡,太小收敛会很缓慢。
- 容易陷入局部最优解(局部极小值)
解决异或问题
如果出现线性不可分问题时,采用的方法是用多个线性函数对区域进行划分,然后对各个神经元的输出作逻辑运算。可以用两条直线实现异或逻辑。
另一个方法是对神经元添加非线性输入,引入非线性成分。如下图是我们解决异或问题的模型图,引入了非线性成分来解决。
如上图,我们可以写出表达式
x0w0+x1w1+x2w2+x1^2w3+x1x2w4+x2^2w5 = 0 将x0 = 1以及x1 = x,x2 =y带入
w0+xw1+yw2+x^2w3+xyw4+y^2w5 = 0 整理得
w5y^2+y(w2+xw4)+w0+xw1+x^2w3 = 0
a =w5,b=w2+xw4,c=w0+xw1+x^2w3
由二次方求根公式y = [-b±√(b^2-4*a*c)]/(2*a)可以求得根。
代码实现:
- 导入需要用到的包
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline- 输入数据、标签、初始化权值、设置学习率以及更新权值函数
#输入数据
X = np.array([[1,0,0,0,0,0],
[1,0,1,0,0,1],
[1,1,0,1,0,0],
[1,1,1,1,1,1]])
#标签
Y = np.array([-1,1,1,-1])
#权值初始化,3行1列,取值范围-1到1
W = (np.random.random(6)-0.5)*2
print(W)
#学习率设置
lr = 0.11
#神经网络输出
O = 0
def update():
global X,Y,W,lr
O = np.dot(X,W) # shape:(3,1)
W_C = lr*(X.T.dot(Y-O))/int(X.shape[0])
W = W + W_C- 设置非线性函数以及显示模型的最终结果(在这里实现模型,我们用到的是:设定最大迭代次数,当迭代超过最大次数就停止的条件作为模型的收敛。)
for _ in range(10000):
update()#更新权值
# 正样本
x1 = [0,1]
y1 = [1,0]
#负样本
x2 = [1,0]
y2 = [1,0]
xdata = np.linspace(-1,2)
def calculate(x,root):
a = W[5]
b = W[2]+x*W[4]
c = W[0]+x*W[1]+x*x*W[3]
if root==1:
return (-b+np.sqrt(b*b-4*a*c))/(2*a)
if root==2:
return (-b-np.sqrt(b*b-4*a*c))/(2*a)
plt.figure()
plt.plot(xdata,calculate(xdata,1),'r')
plt.plot(xdata,calculate(xdata,2),'r')
plt.scatter(x1,y1,c='b')
plt.scatter(x2,y2,c='y')
plt.show()
显示结果:
我们可以清楚的看到,已经成功的将我们线性不可分的点分割开。