《数据结构》-二叉树(二叉链表实现)
静态数组实现二叉树
二叉链表实现二叉树
三叉链表实现二叉树
线索二叉树
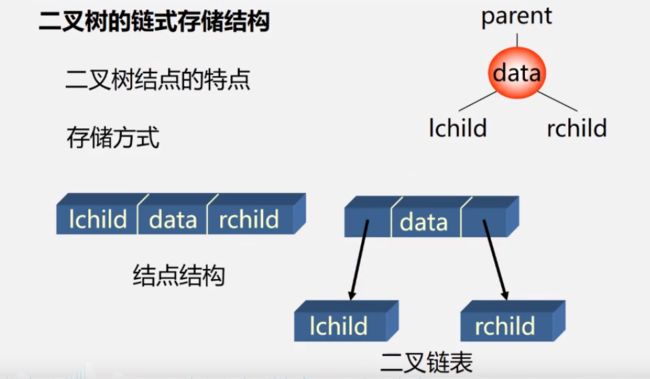
二叉链表存储特点
// 二叉树的二叉链表存储表示
typedef struct BiTNode
{
TElemType data;
struct BiTNode *lchild, *rchild; // 左右孩子指针
} BiTNode, *BiTree;
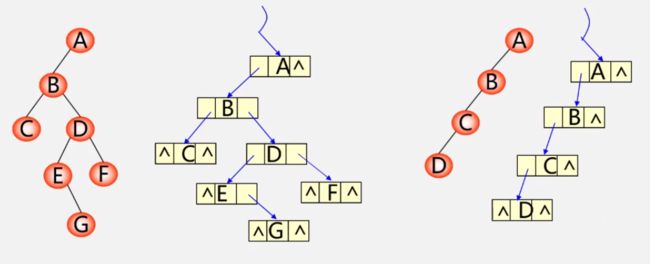
存储示例
代码实现
main.c
/*
* Change Logs:
* Date Author Notes
* 2021-07-20 tyustli first version
*/
#include "tree.h"
void visitT(TElemType e)
{
printf("%d ", e);
}
int main(int argc, char *argv[])
{
printf("this bitree\r\n");
int i;
BiTree T, p, c;
TElemType e1, e2;
InitBiTree(&T);
printf("构造空二叉树后,树空否? %d(1 : 是 0: 否) 树的深度 = %d \n", BiTreeEmpty(T), BiTreeDepth(T));
e1 = Root(T);
if (e1)
printf("二叉树的根为: %d \n", e1);
else
printf("树空,无根 \n");
printf("请先序输入二叉树(如:1 2 0 0 0表示1为根结点,2为左子树的二叉树)\n");
CreateBiTree(&T);
printf("建立二叉树后,树空否?%d(1:是 0:否) 树的深度=%d\n", BiTreeEmpty(T), BiTreeDepth(T));
e1 = Root(T);
if (e1)
printf("二叉树的根为: %d \n", e1);
else
printf("树空,无根\n");
printf("\n先序递归遍历二叉树:\n");
PreOrderTraverse(T, visitT);
printf("\n中序递归遍历二叉树:\n");
InOrderTraverse1(T, visitT);
InOrderTraverse2(T, visitT);
InOrderTraverse3(T, visitT);
printf("\n后序递归遍历二叉树:\n");
PostOrderTraverse(T, visitT);
}
/*
1
2 3
0 0 0 0
编译:make
运行:./obj
结果:
this bitree
构造空二叉树后,树空否? 1(1 : 是 0: 否) 树的深度 = 0
树空,无根
请先序输入二叉树(如:1 2 0 0 0表示1为根结点,2为左子树的二叉树)
1
2
0
0
3
0
0
建立二叉树后,树空否?0(1:是 0:否) 树的深度=2
二叉树的根为: 1
先序递归遍历二叉树:
1 2 3
中序递归遍历二叉树:
2 1 3
2 1 3
2 1 3
后序递归遍历二叉树:
2 3 1
*/
/***************** end of file ******************/
tree.c
#include "tree.h"
#define ClearBiTree DestroyBiTree // 清空二叉树和销毁二叉树的操作一样
TElemType Nil = 0; // 设整型以0为空
// 操作结果:构造空二叉树T
void InitBiTree(BiTree *T)
{
*T = NULL;
}
// 按先序次序输入二叉树中结点的值(可为字符型或整型,在主程中定义),
// 构造二叉链表表示的二叉树T。变量 Nil 表示空(子)树。有改动
void CreateBiTree(BiTree *T)
{
TElemType ch;
scanf("%d", &ch);
if (ch == Nil) // 空
{
*T = NULL;
}
else
{
*T = (BiTree)malloc(sizeof(BiTNode)); // 生成根结点
if (!*T)
{
printf("create bitree malloc failed\r\n");
exit(-1);
}
(*T)->data = ch;
CreateBiTree(&(*T)->lchild); // 构造左子树
CreateBiTree(&(*T)->rchild); // 构造右子树
}
}
// 初始条件:二叉树T存在。
// 操作结果:销毁二叉树T
void DestroyBiTree(BiTree *T)
{
if (*T) // 非空树
{
if ((*T)->lchild) // 有左孩子
DestroyBiTree(&(*T)->lchild); // 销毁左孩子子树
if ((*T)->rchild) // 有右孩子
DestroyBiTree(&(*T)->rchild); // 销毁右孩子子树
free(*T); // 释放根结点
*T = NULL; // 空指针赋0
}
}
// 初始条件:二叉树T存在。
// 操作结果:若T为空二叉树,则返回TRUE,否则FALSE
Status BiTreeEmpty(BiTree T)
{
if (T)
return FALSE;
else
return TRUE;
}
// 初始条件:二叉树T存在。
// 操作结果:返回T的深度
int BiTreeDepth(BiTree T)
{
int i, j;
if (!T)
return 0; // 空树深度为0
if (T->lchild)
i = BiTreeDepth(T->lchild); // i为左子树的深度
else
i = 0;
if (T->rchild)
j = BiTreeDepth(T->rchild); // j为右子树的深度
else
j = 0;
return i > j ? i + 1 : j + 1; // T的深度为其左右子树的深度中的大者+1
}
// 初始条件:二叉树T存在。
// 操作结果:返回T的根
TElemType Root(BiTree T)
{
if (BiTreeEmpty(T))
return Nil;
else
return T->data;
}
// 初始条件:二叉树 T 存在,p 指向 T 中某个结点。
// 操作结果:返回 p 所指结点的值
TElemType Value(BiTree p)
{
return p->data;
}
// 给 p 所指结点赋值为 value
void Assign(BiTree p, TElemType value)
{
p->data = value;
}
#if 1
typedef BiTree QElemType;
typedef struct QNode
{
QElemType data; /* 数据域 */
struct QNode *next; /* 指针域 */
} QNode, *QueuePtr;
typedef struct LinkQueue
{
QueuePtr front; // 队头指针
QueuePtr rear; // 队尾指针
} LinkQueue;
void InitQueue(LinkQueue *Q);
void DestroyQueue(LinkQueue *Q);
void ClearQueue(LinkQueue *Q);
Status QueueEmpty(LinkQueue Q);
int QueueLength(LinkQueue Q);
Status GetHead(LinkQueue Q, QElemType *e);
void EnQueue(LinkQueue *Q, QElemType e);
Status DeQueue(LinkQueue *Q, QElemType *e);
void QueueTraverse(LinkQueue Q, void (*vi)(QElemType));
void print(QElemType i);
/*
队列的链式表示和实现
若用户无法估计所用队列的长度,则宜采用链队列
*/
// 链队列的基本操作 (9个)
void InitQueue(LinkQueue *Q)
{ // 构造一个空队列 Q
Q->front = Q->rear = (QueuePtr)malloc(sizeof(QNode)); /* 单链表的头结点 */
if (Q->front == NULL)
exit(-1);
Q->front->next = NULL;
}
/* 算法思想
从头结点开始,依次释放所有结点
*/
void DestroyQueue(LinkQueue *Q)
{ // 销毁队列 Q (无论空否均可)
while (Q->front)
{
Q->rear = Q->front->next;
free(Q->front);
Q->front = Q->rear;
}
}
void ClearQueue(LinkQueue *Q)
{ // 将Q清为空队列
QueuePtr p, q;
Q->rear = Q->front;
p = Q->front->next;
Q->front->next = NULL;
while (p)
{
q = p;
p = p->next;
free(q);
}
}
Status QueueEmpty(LinkQueue Q)
{ // 若 Q 为空队列,则返回 TRUE,否则返回 FALSE
if (Q.front->next == NULL)
return TRUE;
else
return FALSE;
}
int QueueLength(LinkQueue Q)
{ // 求队列的长度
int i = 0;
QueuePtr p;
p = Q.front;
while (Q.rear != p)
{
i++;
p = p->next;
}
return i;
}
Status GetHead(LinkQueue Q, QElemType *e)
{ // 若队列不空,则用 e 返回 Q 的队头元素,并返回 OK,否则返回 ERROR
QueuePtr p;
if (Q.front == Q.rear)
return ERROR;
p = Q.front->next;
*e = p->data;
return OK;
}
void EnQueue(LinkQueue *Q, QElemType e)
{ // 插入元素 e 为 Q 的新的队尾元素
QueuePtr p;
if (!(p = (QueuePtr)malloc(sizeof(QNode)))) // 存储分配失败
exit(-1);
p->data = e;
p->next = NULL; /* 新结点的 next 为空 */
Q->rear->next = p; /* 上一次的尾指针指向新的结点 */
Q->rear = p; /* 新的尾指针 */
}
Status DeQueue(LinkQueue *Q, QElemType *e)
{ // 若队列不空,删除 Q 的队头元素,用e返回其值,并返回 OK,否则返回 ERROR
QueuePtr p;
if (Q->front == Q->rear)
return ERROR;
p = Q->front->next;
*e = p->data;
Q->front->next = p->next;
if (Q->rear == p)
Q->rear = Q->front;
free(p);
return OK;
}
void QueueTraverse(LinkQueue Q, void (*vi)(QElemType))
{ // 从队头到队尾依次对队列 Q 中每个元素调用函数 vi()
QueuePtr p;
p = Q.front->next;
while (p)
{
vi(p->data);
p = p->next;
}
printf("\n");
}
void print(QElemType i)
{
// printf("%s ", i);
}
/****************************** end of file **********************************/
#endif
// typedef BiTree QElemType; 设队列元素为二叉树的指针类型
// 初始条件:二叉树T存在,e是T中某个结点
// 操作结果:若e是T的非根结点,则返回它的双亲,否则返回"空"
TElemType Parent(BiTree T, TElemType e)
{
LinkQueue q;
QElemType a;
if (T) // 非空树
{
InitQueue(&q); // 初始化队列
EnQueue(&q, T); // 树根指针入队
while (!QueueEmpty(q)) // 队不空
{
DeQueue(&q, &a); // 出队,队列元素赋给a
if (a->lchild && a->lchild->data == e || a->rchild && a->rchild->data == e) // 找到e(是其左或右孩子)
return a->data; // 返回e的双亲的值
else // 没找到e,则入队其左右孩子指针(如果非空)
{
if (a->lchild)
EnQueue(&q, a->lchild);
if (a->rchild)
EnQueue(&q, a->rchild);
}
}
}
return Nil; // 树空或没找到e
}
// 返回二叉树T中指向元素值为s的结点的指针。另加
BiTree Point(BiTree T, TElemType s)
{
LinkQueue q;
QElemType a;
if (T) // 非空树
{
InitQueue(&q); // 初始化队列
EnQueue(&q, T); // 根指针入队
while (!QueueEmpty(q)) // 队不空
{
DeQueue(&q, &a); // 出队,队列元素赋给a
if (a->data == s)
return a;
if (a->lchild) // 有左孩子
EnQueue(&q, a->lchild); // 入队左孩子
if (a->rchild) // 有右孩子
EnQueue(&q, a->rchild); // 入队右孩子
}
}
return NULL;
}
// 初始条件:二叉树 T 存在,e 是 T 中某个结点。
// 操作结果:返回 e 的左孩子。若 e 无左孩子,则返回"空"
TElemType LeftChild(BiTree T, TElemType e)
{
BiTree a;
if (T) // 非空树
{
a = Point(T, e); // a 是结点 e 的指针
if (a && a->lchild) // T 中存在结点 e 且 e 存在左孩子
return a->lchild->data; // 返回e的左孩子的值
}
return Nil; // 其余情况返回空
}
// 初始条件:二叉树 T 存在,e 是 T 中某个结点。
// 操作结果:返回 e 的右孩子。若 e 无右孩子,则返回"空"
TElemType RightChild(BiTree T, TElemType e)
{
BiTree a;
if (T) // 非空树
{
a = Point(T, e); // a是结点e的指针
if (a && a->rchild) // T中存在结点e且e存在右孩子
return a->rchild->data; // 返回e的右孩子的值
}
return Nil; // 其余情况返回空
}
// 初始条件:二叉树 T 存在,e 是 T 中某个结点
// 操作结果:返回 e 的左兄弟。若 e 是 T 的左孩子或无左兄弟,则返回"空"
TElemType LeftSibling(BiTree T, TElemType e)
{
TElemType a;
BiTree p;
if (T) // 非空树
{
a = Parent(T, e); // a为e的双亲
if (a != Nil) // 找到e的双亲
{
p = Point(T, a); // p为指向结点a的指针
if (p->lchild && p->rchild && p->rchild->data == e) // p存在左右孩子且右孩子是e
return p->lchild->data; // 返回p的左孩子(e的左兄弟)
}
}
return Nil; // 其余情况返回空
}
// 初始条件:二叉树T存在,e是T中某个结点
// 操作结果:返回e的右兄弟。若e是T的右孩子或无右兄弟,则返回"空"
TElemType RightSibling(BiTree T, TElemType e)
{
TElemType a;
BiTree p;
if (T) // 非空树
{
a = Parent(T, e); // a为e的双亲
if (a != Nil) // 找到e的双亲
{
p = Point(T, a); // p为指向结点a的指针
if (p->lchild && p->rchild && p->lchild->data == e) // p存在左右孩子且左孩子是e
return p->rchild->data; // 返回p的右孩子(e的右兄弟)
}
}
return Nil; // 其余情况返回空
}
// 初始条件:二叉树T存在,p指向T中某个结点,LR为0或1,非空二叉树c与T不相交且右子树为空
// 操作结果:根据LR为0或1,插入c为T中p所指结点的左或右子树。p所指结点的
// 原有左或右子树则成为c的右子树
Status InsertChild(BiTree p, int LR, BiTree c) // 形参T无用
{
if (p) // p不空
{
if (LR == 0)
{
c->rchild = p->lchild;
p->lchild = c;
}
else // LR==1
{
c->rchild = p->rchild;
p->rchild = c;
}
return OK;
}
return ERROR; // p空
}
// 初始条件:二叉树T存在,p指向T中某个结点,LR为0或1
// 操作结果:根据LR为0或1,删除T中p所指结点的左或右子树
Status DeleteChild(BiTree p, int LR) // 形参T无用
{
if (p) // p不空
{
if (LR == 0) // 删除左子树
ClearBiTree(p->lchild);
else // 删除右子树
ClearBiTree(p->rchild);
return OK;
}
return ERROR; // p空
}
#if 1
typedef BiTree SElemType; // 定义栈元素类型为整型
#define STACK_INIT_SIZE 10 // 存储空间初始分配量
#define STACK_INCREMENT 2 // 存储空间分配增量
typedef struct SqStack
{
SElemType *top;
SElemType *base;
int stacksize;
} SqStack;
void InitStack(SqStack *S)
{
S->base = (SElemType *)malloc(STACK_INIT_SIZE * sizeof(SElemType));
if (!(S->base))
exit(-1); // 存储分配失败
S->top = S->base;
S->stacksize = STACK_INIT_SIZE;
return;
}
void DestroyStack(SqStack *S)
{
free(S->base);
S->base = NULL;
S->top = NULL;
S->stacksize = 0;
return;
}
void ClearStack(SqStack *S)
{
if (S->base)
S->top = S->base;
return;
}
Status StackEmpty(SqStack S)
{
if (S.top == S.base)
return TRUE;
else
return FALSE;
}
int StackLength(SqStack S)
{
return S.top - S.base;
}
/* 获取栈顶元素 */
Status GetTop(SqStack S, SElemType *e)
{
if (S.top > S.base)
{
*e = *(S.top - 1);
return OK;
}
else
{
return ERROR;
}
}
void Push(SqStack *S, SElemType e)
{
if (S->top - S->base >= S->stacksize) // 栈满,追加存储空间
{
S->base = (SElemType *)realloc(S->base, (S->stacksize + STACK_INCREMENT) * sizeof(SElemType));
if (!(S->base))
exit(-1); // 存储分配失败
S->top = S->base + S->stacksize;
S->stacksize += STACK_INCREMENT;
}
*(S->top)++ = e;
}
Status Pop(SqStack *S, SElemType *e)
{
if (S->top == S->base)
return ERROR;
*e = *--(S->top);
return OK;
}
void StackTraverse(SqStack S, void (*visit)(SElemType))
{
while (S.top > S.base)
visit(*S.base++);
printf("\n");
}
#endif
// typedef BiTree SElemType; // 设栈元素为二叉树的指针类型
// 采用二叉链表存储结构,Visit是对数据元素操作的应用函数。算法6.3,有改动
// 中序遍历二叉树T的非递归算法(利用栈),对每个数据元素调用函数Visit
void InOrderTraverse1(BiTree T, void (*Visit)(TElemType))
{
SqStack S;
InitStack(&S);
while (T || !StackEmpty(S))
{
if (T)
{ // 根指针进栈,遍历左子树
Push(&S, T);
T = T->lchild;
}
else
{ // 根指针退栈,访问根结点,遍历右子树
Pop(&S, &T);
Visit(T->data);
T = T->rchild;
}
}
printf("\n");
}
// 采用二叉链表存储结构,Visit是对数据元素操作的应用函数。算法6.2,有改动
// 中序遍历二叉树T的非递归算法(利用栈),对每个数据元素调用函数Visit
void InOrderTraverse2(BiTree T, void (*Visit)(TElemType))
{
SqStack S;
BiTree p;
InitStack(&S);
Push(&S, T); // 根指针进栈
while (!StackEmpty(S))
{
while (GetTop(S, &p) && p)
Push(&S, p->lchild); // 向左走到尽头
Pop(&S, &p); // 空指针退栈
if (!StackEmpty(S))
{ // 访问结点,向右一步
Pop(&S, &p);
Visit(p->data);
Push(&S, p->rchild);
}
}
printf("\n");
}
// 初始条件:二叉树T存在,Visit是对结点操作的应用函数
// 操作结果:中序递归遍历T,对每个结点调用函数Visit一次且仅一次
void InOrderTraverse3(BiTree T, void (*Visit)(TElemType))
{
if (T) // T不空
{
InOrderTraverse3(T->lchild, Visit); // 先中序遍历左子树
Visit(T->data); // 再访问根结点
InOrderTraverse3(T->rchild, Visit); // 最后中序遍历右子树
}
}
// 初始条件:二叉树T存在,Visit是对结点操作的应用函数
// 操作结果:后序递归遍历T,对每个结点调用函数Visit一次且仅一次
void PostOrderTraverse(BiTree T, void (*Visit)(TElemType))
{
if (T) // T不空
{
PostOrderTraverse(T->lchild, Visit); // 先后序遍历左子树
PostOrderTraverse(T->rchild, Visit); // 再后序遍历右子树
Visit(T->data); // 最后访问根结点
}
}
// 初始条件:二叉树T存在,Visit是对结点操作的应用函数。算法6.1,有改动
// 操作结果:先序递归遍历T,对每个结点调用函数Visit一次且仅一次
void PreOrderTraverse(BiTree T, void (*Visit)(TElemType))
{
if (T) // T不空
{
Visit(T->data); // 先访问根结点
PreOrderTraverse(T->lchild, Visit); // 再先序遍历左子树
PreOrderTraverse(T->rchild, Visit); // 最后先序遍历右子树
}
}
// 初始条件:二叉树T存在,Visit是对结点操作的应用函数
// 操作结果:层序递归遍历T(利用队列),对每个结点调用函数Visit一次且仅一次
void LevelOrderTraverse(BiTree T, void (*Visit)(TElemType))
{
LinkQueue q;
QElemType a;
if (T)
{
InitQueue(&q); // 初始化队列q
EnQueue(&q, T); // 根指针入队
while (!QueueEmpty(q)) // 队列不空
{
DeQueue(&q, &a); // 出队元素(指针),赋给a
Visit(a->data); // 访问a所指结点
if (a->lchild != NULL) // a有左孩子
EnQueue(&q, a->lchild); // 入队a的左孩子
if (a->rchild != NULL) // a有右孩子
EnQueue(&q, a->rchild); // 入队a的右孩子
}
printf("\n");
}
}
/***************** end of file ******************/
tree.h
/*
* Change Logs:
* Date Author Notes
* 2021-07-20 tyustli first version
*/
#include makefile
objects = main.o tree.o
obj: $(objects)
cc -o obj $(objects) -lm
main.o : tree.h
tree.o : tree.h
.PHONY : clean
clean :
-rm obj $(objects)