Day39 力扣动态规划 :139.单词拆分 |关于多重背包,你该了解这些! |背包问题总结篇!
Day39 力扣动态规划 :139.单词拆分 |关于多重背包,你该了解这些! |背包问题总结篇!
- 139.单词拆分
-
- 第一印象
- 看完题解的思路
-
- dp数组
- 递推公式
- 初始化
- 遍历顺序
- 实现中的困难
- 感悟
-
- 为什么这道题一定要先背包再物品
- 代码
- 关于多重背包,你该了解这些!
-
- 看完题解的思路
- 感悟
- 背包问题总结篇!
-
- 概述
- 回顾题干怎么问的
- 总结
-
- dp数组
- 递推公式
- 初始化
- 遍历顺序
- 一些感悟
-
- 01背包为什么逆序
- 背包问题如何初始化
- 问多少种方法的背包问题,为什么递推公式是累加啊?
-
- 二维角度理解递推公式
- 一维角度理解递推公式
- 完全背包为什么正序遍历可以反复加入一个元素呢?
- 为什么纯粹完全背包,两层for循环可以颠倒呢?
- 为什么先物品再背包是组合,先背包再物品是排列?
-
- 先物品在背包
- 先背包再物品
- 总结
- 打日志
- 零钱兑换1 和 2的区别
- 对for循环顺序是怎么产生排列 、组合
详细布置
关于 多重背包,力扣上没有相关的题目,所以今天大家的重点就是回顾一波 自己做的背包题目吧。
139.单词拆分
视频讲解:https://www.bilibili.com/video/BV1pd4y147Rh
https://programmercarl.com/0139.%E5%8D%95%E8%AF%8D%E6%8B%86%E5%88%86.html
第一印象
又遇到要用字符串的算法了啊啊啊啊
讨厌字符串,记不住操作,操作还麻烦。
我先试试
这道题的背包是目标字符串,物品是词典,词典中的东西可以无限使用,所以算是完全背包。
写完了,感觉逻辑问题不大,但是字典里有彼此的子集的时候就不好弄了。
比如目标 aaaaaaa
字典是 aaaa aaa
就会出现6个a的时候当做aaa+aaa
到第七个a就不好使了的情况
啊我知道了,我本来还觉得这道题不怎么背包,应该有一个[j - weight[i]] 的过程。
但是这个背包不像之前,容量为 1 2 3……
s的子串可能性很多,怎么遍历背包呢,直接看题解吧。
先把我自己的错代码放上来
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
boolean[] dp = new boolean[s.length()];
Arrays.fill(dp, false);
int start = 0;
for (int j = start; j < dp.length; j++) {
String target = s.substring(start, j + 1);
for (int i = 0; i < wordDict.size(); i++) {
if (wordDict.get(i).equals(target)) {
dp[j] = true;
start = j + 1;
}
}
for(int k = 0; k < dp.length; k++) {
System.out.print(dp[k] + " ");
}
System.out.println();
}
return dp[s.length() - 1];
}
}
又寻思了一下,递推公式想这么写,也不行
//递推公式
for (int i = 0; i < wordDict.size(); i++) {
for (int j = wordDict.get(i).length(); j < dp.length; j++) {
String sub = s.substring(j - wordDict.get(i).length(), j);
if (wordDict.get(i).equals(sub)) {
dp[j] = dp[j - wordDict.get(i).length()] | dp[j];
}
}
//打印dp
for(int k = 0; k < dp.length; k++) {
System.out.print(dp[k] + " ");
}
System.out.println();
}
看完题解的思路
悟了,物品根本不是字典。物品是截取出来的子串。
首先是个完全背包,那么组合还是排列呢?applepenapple的字符串如果想被{ apple, pen }组成,那么必须是1 2 1的顺序,112组成不了。所以这道题和顺序有关系。 而且是排列,所以先背包后物品
dp数组
字符串s,长度为 1 ~ i 的子串是dp[i] (true能,false不能)组成的。
递推公式
如果dp[j] 是true,那么[j, I] 的子串还在字典里,则dp[i] 就是true。
这个递推公式好奇怪没见过。
初始化
do[0] 没有意义,因为题目说了给的 s 一定是非空的。
所以为了配合递推公式dp[0] 是 true,其他都是 false
遍历顺序
先背包后物品,正序
实现中的困难
思路清晰之后实现就没困难
感悟
题解说这道题和回溯的 分割回文子串很像 但我已经忘了哈哈哈,二刷再说吧。
这道题难在这个递推公式
也难在怎么认识“物品”的概念,其实物品也是字典,只是这个物品放进去的过程和前面是不一样的,但我也说不上哪不一样。
为什么这道题一定要先背包再物品
代码随想录里这段说得很好,很能讲清遍历顺序的不同是怎么出现排列和组合的。
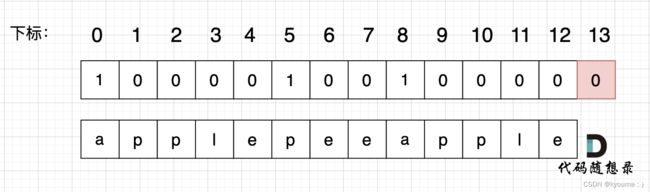
最后dp[s.size()] = 0 即 dp[13] = 0 ,而不是1,因为先用 “apple” 去遍历的时候,dp[8]并没有被赋值为1 (还没用"pen"),所以 dp[13]也不能变成1。
这里和我之前分析排列和组合是怎么产生的很像,因为还没用2,所以和是2的情况只有 1 1,所以和是3的时候,再拿来2也只能出现 1 2 和 111. 如果是排列,用1遍历一遍,也用2遍历了一遍,和是2的情况就有 11 和 2,这样和是3的时候就有 111 21 12 了。
除非是先用 “apple” 遍历一遍,再用 “pen” 遍历,此时 dp[8]已经是1,最后再用 “apple” 去遍历,dp[13]才能是1
代码
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
HashSet<String> set = new HashSet<>(wordDict);
boolean[] dp = new boolean[s.length() + 1];
Arrays.fill(dp, false);
dp[0] = true;
//递推公式,先背包后物品
for (int j = 1; j < dp.length; j++) {
for (int i = 0; i < j; i++) {
//取子串
//这个范围要举个例子洗洗看,substring() 函数左闭右开
String sub = s.substring(i, j);
if (set.contains(sub) && dp[i]) {
dp[j] = true;
}
}
}
return dp[s.length()];
}
}
关于多重背包,你该了解这些!
https://programmercarl.com/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80%E5%A4%9A%E9%87%8D%E8%83%8C%E5%8C%85.html
看完题解的思路
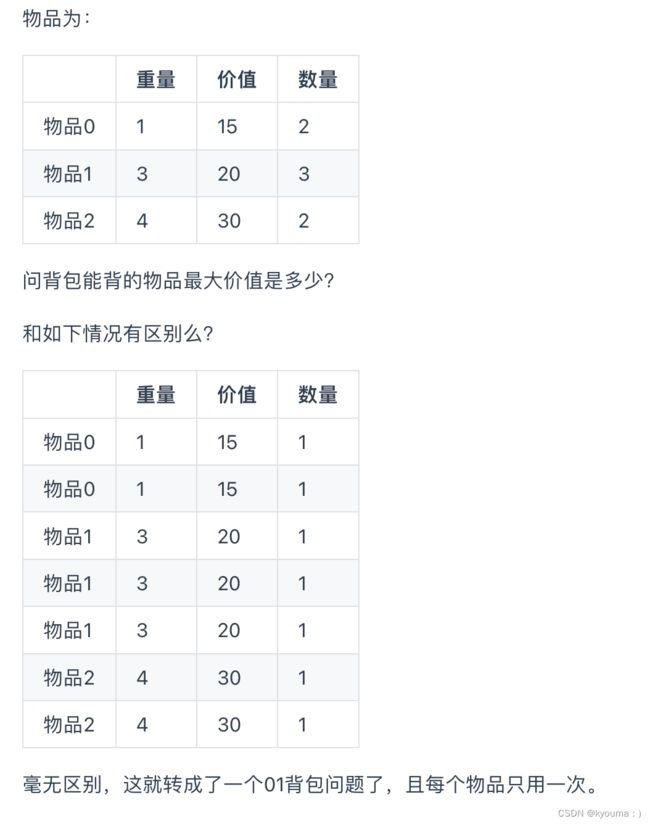
多重背包就是每个物品是有限数量的背包。
多重背包和01背包是非常像的, 为什么和01背包像呢?
每件物品最多有Mi件可用,把Mi件摊开,其实就是一个01背包问题了。
确实,把数组变大,每个都是1件。
感悟
代码随想录说:
多重背包在面试中基本不会出现,力扣上也没有对应的题目,大家对多重背包的掌握程度知道它是一种01背包,并能在01背包的基础上写出对应代码就可以了。
至于背包九讲里面还有混合背包,二维费用背包,分组背包等等这些,大家感兴趣可以自己去学习学习,这里也不做介绍了,面试也不会考。
背包问题总结篇!
https://programmercarl.com/%E8%83%8C%E5%8C%85%E6%80%BB%E7%BB%93%E7%AF%87.html
概述
做背包问题五步走:
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
第一个难点在于,透过题目分析出是个背包问题
找到背包和物品,背包的大小,物品的重量和价值。
回顾题干怎么问的
回顾之前的背包
- 01背包基础:背包尽量装,问最大价值
- 分割相等子集:背包尽量装,问能不能装满,也就是**最大重量(价值)**满不满
- 最后一个石头:背包尽量装,问最大重量(价值)
- 目标和:给一个01背包,问装满有多少种方法
- 一和零: 给一个背包,有两个维度,尽量装,问背包需要物品的最大个数
- 完全背包基础:背包尽量装,问最大价值
- 零钱兑换2:给一个完全背包,问装满有多少种方法,这道题是组合
- 组合总和5:给一个完全背包,问装满有多少种方法,这道题是排列
- 爬楼梯:给一个完全背包,问装满有多少种方法,这道题是排列
- 零钱兑换:给一个完全背包,问装满背包需要物品的最小个数
- 完全平方数:给一个完全背包,问装满背包需要物品的最小个数
- 单词拆分:奇怪的一道题但也是完全背包,它的递推公式很奇怪。
总结
dp数组
dp数组的含义要清晰,一般直接拿问题的含义来定义这个数组。
递推公式
有三种,求最大、求最小、求方法数量。
- 求最大:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
- 求最小:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
- 求方法数量:dp[j] += dp[j - nums[i]]
对于重量和价值要灵活运用,有的时候value[i] 就是weight[i] (价值就是属性B的重量),有的时候是 1 (求物品个数的题)等等。
熟练之后应该直接拿来用,而不是再细细分析了,比如问求方法数量的题,直接把这个公式拿来就行。
初始化
要自己分析初始化,一般不难。
主要是dp[0]
遍历顺序
- 01背包都是逆序,先物品再背包
- 完全背包都是正序,先物品再背包是组合,先背包再物品是排列
一些感悟
我在思考背包问题的时候,有一些拐不过弯的点,进行了一些思考
都散落在每个题解里,这里汇总一下。
01背包为什么逆序
在二维的时候,我们正序遍历。
但在一维的时候,我们要倒序遍历。先给出结论
记住公式 dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
举上面的例子,
物品0在 j=1 的时候,dp[1] = max( dp[1], dp[0] + value[0] ) = max (0, 0+15) = 15. 合理
物品0在 j=2 的时候,dp[2] = max ( dp[2], dp[1] + value[0] ) = max (0, 30) = 30. 这就不合理了
这道题每个物品只能用一次
物品0大小是 1,那么背包容量j=2的时候,应该还是1个物品0的价值15。
但是正序遍历会让递推公式在计算价值的时候,把物品0的价值在 j=1 的时候和 j=2 的时候加在一起。
数值上看确实是不合理的,但是逻辑上呢?
我觉得是这样的,包现在是空的,我们把物品0 往里放,算包的容量如果是 1 2 3 4时候的最大价值。如果能放进去,就是这个物品不放包里时(也就是j - weight[i])包里的价值 + 这件物品的价值。
而这个不放包里时包里的价值应该是 上一件物品在这个 j 的最大价值。如果顺序遍历,比如 j=1 的时候是15,j = 2的时候是15 + 物品的价值15.
这里的第一个15代表容量为 1 时,物品0的最大价值。而不是什么也不放时的最大价值。
举个数量多的例子。
也就是对于重量为 1 的物品 4 来说,他在容量为j=5 的时候,计算的结果应该是,物品0~3 在 j=4 时的最大价值 + 物品4 的最大价值。而不是物品0~4在 j=4 时的最大价值 + 物品4 的价值。
对于物品 i, dp[j] 的数值是基于 0~ i-1 件物品在 j 和 j-weight[i] 的最大价值,也就是这个dp[j] 是用自己和滚动前它左侧的某个数算出来的,所以不能正序遍历,不然它就是基于滚动后左侧的某个数 和 自己算出来的了。就不对了。滚动后左侧的数会让它自己反复的加了多次,感到疑惑的话就拿题解里的例子画一画就行了
所以要倒序遍历背包容量 j。这样dp[j] 就可以基于滚动前 左侧数值求出了。
背包问题如何初始化
上面是我从产生疑问 到 解决疑问的思路过程。
总之,我基于我和滚动前左边的数算出来的,那么求我之前,我左面的数不能求。所以倒序
我好像找到了规律,首先要画出来方便理解
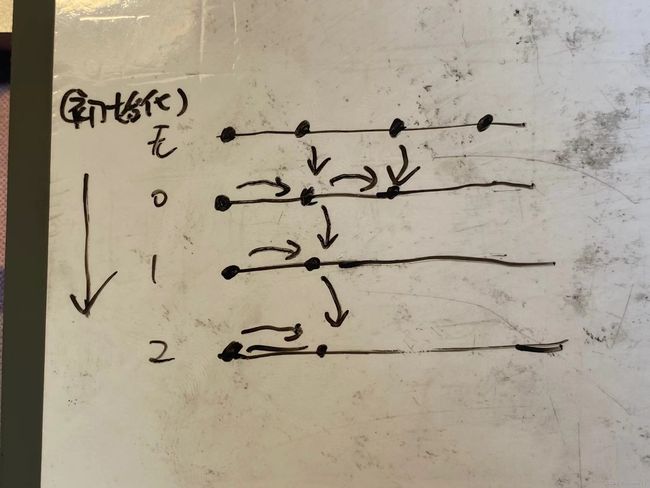
1.机器人格子那道题,每个格子由上面和左边的格子求出来,所以初始化要第一行和第一列。而遍历的时候无所谓,一行一行,一列一列都可以。如图
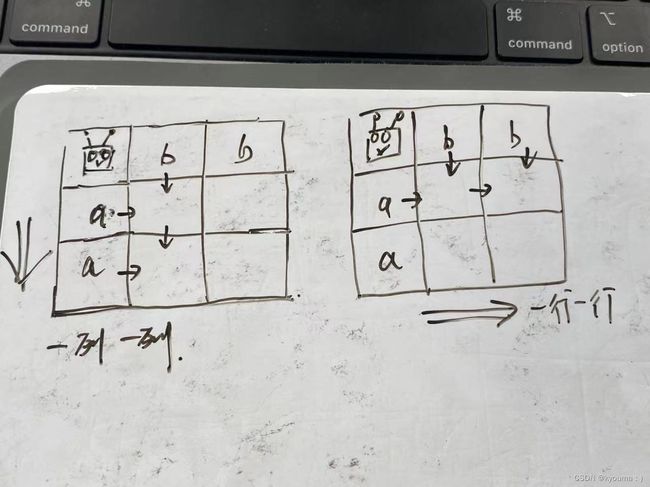
2.二维dp的背包,每个数字由上面的和左上方的某个求出来,所以初始化的时候要第一行和第一列。而遍历的时候,也无所谓,每个数都是由上一行和左上方数求出来的。如图
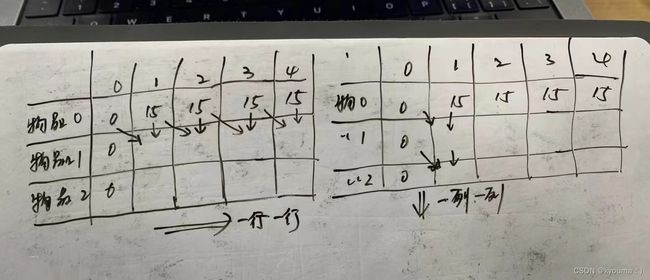
3.一维dp的背包,每个数字基于自己和滚动前左面的某个(就是二维压缩后的结果)。所以初始化要控制自己很小,和初始化dp[0]。而遍历的时候,只能从后向前才能达到图里的样子。
问多少种方法的背包问题,为什么递推公式是累加啊?
我可以从二维dp数组的角度去理解这个累加,但我不太理解一维数组,卡哥讲的那种累加。
二维角度理解递推公式
如图
![]()
去画这个二维数组的过程中就感受到累加的意义了。
比如放入第三个物品(第三个1,图里的1.3)时,想要装满容量为 2的背包(j = 2)有多少种方法?
我拿到了第三个物品,重量是1. 此时第三个物品有两个状态,放入背包和不放入背包。
如果放入背包,就类似上楼梯的问题(联想一下),这个物品已经确定下来了,剩下的背包空间是 1。 问题转换成了,用前两个物品来放,放满容量为 1 的背包有多少种可能? 也就是dp[2 - 1] = dp[1]
如果没有放入背包, 问题转换成了,用前两个物品来放,放满容量为 2 的背包有多少种可能? 也就是dp[2]
那么这三个物品放满容量为 2 的背包有多少种可能呢?就是
dp[2] = dp[2 - 1] + dp[2],dp[2] += dp[2 - 1]
也就是我图里写的,3个1凑2有多少种?2个1 凑1种 + 2个1凑2种
这个例子全都是 1 ,让人感觉有点不和谐。
一维角度理解递推公式
dp[j] += dp[j - nums[i]]
![]()
上面这两个图,我不理解为什么 5 = 4+……+0
而是在滚动更新的过程中,我拿到第i个数,装满容量为 j 的包。依赖于用第i个数的种数和不用它的种数之和,用它就是dp[j - nums[i]],不用就是dp[j]
对比一下最大价值那种,滚动更新的过程中,我拿到第i个物品,装进容量为j的包。包内的最大价值 依赖于 用它装的价值 和 不用他装的价值,更大的那个。所以是 max()。
完全背包为什么正序遍历可以反复加入一个元素呢?
之前的逆序:

从后往前,j=4的时候看容量够不够装下物品0
够,那么就是不装物品0的j=4,和物品0 + 不装物品0的j=3
j=3的时候看容量够不够装下物品0
够,那么就比较不装物品0的j=3,和物品0+不装物品0的j=2
从前往后,j=1的时候看容量够不够装下物品0
够,那么就是不装物品0的j=1,和物品0+不装物品0的j=0.
对于这个例子就是 j[1] = 15
j=2的时候看容量够不够装下物品0
够,那么就是不装物品0的j=2,和物品0+不装物品0的j=1.
而j[1] 已经是 15了,对于这个例子j[2] = 15 + j[1] = 15 + 15 =30
就实现了物品0 放进背包两次。
每个数据是基于滚动前的自己和滚动后的左面。
也就是对于0~i个物品来说,背包的容量为 j 时,这个第 i 个物品有两种状态,放进去和没放进去。
如果没放进去(容量不够放或者不放),背包的最大价值就是0~i-1个物品在容量为 j 时的最大价值: d[j]
如果放进去了,背包的最大价值就是 0~i个物品在容量为 j - weight[i] 时的最大价值 + 物品i的价值。
对比0-1背包, 0~i - 1个物品在容量为 j - weight[i] 时的最大价值 + 物品i的价值。
因为物品 i 可以反复的放。
为什么纯粹完全背包,两层for循环可以颠倒呢?
我理解了。
对于完全背包,用二维数组的视角去看,我是由上面格子,和同一行左面格子算出来的。
所以不管我是一行一行(先物品后背包)去遍历,还是一列一列(先背包后物品)去遍历,到我的时候,我同行的左面和我的上面,都是我需要的数据。
而对于0-1背包,用二维数组的视角去看,我是由上面的格子,和左上方的格子算出来的(上一行的)。
所以我如果一行一行去遍历(当然是倒序的),我就可以获得左上方的正确数据,因为滚动数组还没滚动到那。
但是我如果一列一列(先背包再物品去遍历),我上面的数据是对的,但是我左上方的数据可能是太脏了的,就是我本来需要的是滚动前的,但是那里的确实滚动前前的甚至前前前的,那就太不对了。
为什么先物品再背包是组合,先背包再物品是排列?
先给出结论:就必须先遍历物品,再遍历背包。
对于纯粹的完全背包,问的是最大价值是多少,所以和物品的顺序没有关系,组合也行,排列也行,因为dp数组的含义是最大价值。
而这道题明确要求,只要统计组合,dp数组的含义是组合数。
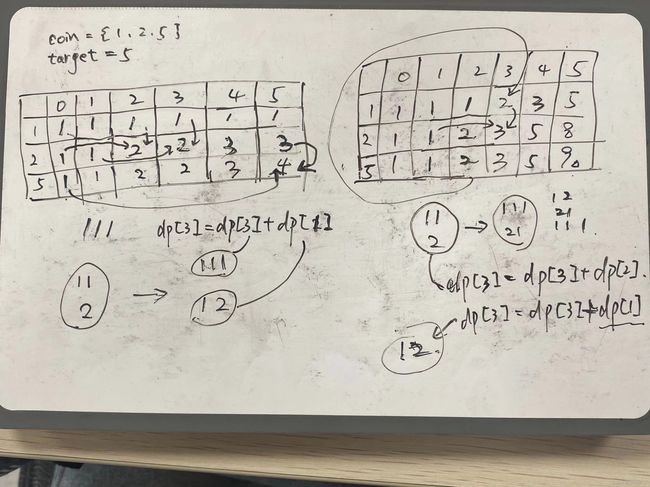
我们做个对比,左边先物品再背包,右边先背包再物品
都拿 2元面值 在容量为3 的时候举例子。
先物品在背包
此时的dp[3] = dp[3] + dp[1]
分析等式右侧:
dp[1] 是拿到一张2元加入背包,这样的话方法数和背包容量为1时候一样,也就是本来只有 1 张 1元的时候,加入后就是 1元 2元 的情况。
dp[3] 是拿到一张2元我不加入背包,这样的话方法数和背包容量为3时候一样,也就是本来只有3张 1元的时候。
所以就是两种,12和111
先背包再物品
此时的dp[3] = dp[3] + dp[1]
分析等式右侧:
dp[1] 和上面是一样的
dp[3]就不一样了,是拿到一张2元我选择不放,这样的话方法数和容量为3时候一样。而这个时候的dp[3]不是三张一元的情况。而是3张1元,1张2元和2张1元的情况。
为什么呢?我们看看原本的dp[3] 怎么来的,它是dp[3] + d[2]。dp[3] 是0,dp[2] 是放入两张1元和一张2元的情况。
总结
也就是说第一行的dp[3] 是基于自己和 j = 2时,计算更新后的dp[2] 计算出来的。
反过来看左边的情况,第一行的dp[3] 是基于自己和 j = 1时算出来的dp[2] 计算出来的。
所以对于先物品的情况,这个dp[2] 是没有考虑 钞票2元的。 因为遍历顺序上没轮到2元。
而对于先背包的情况,这个dp[2] 是考虑了钞票2元的。因为竖着遍历,已经考虑过 如果有2元钞票的话,dp[2] 会是多少了。
总之里外里就是差在,21 这样的情况在左面没出现,在右面出现了,所以左面是组合,右面是排列。
我的理解比较浅薄,只能通过打日志、手动模拟,选取了一个比较好去思考的过程点去分析,至于宏观上为什么一个是组合一个是排列,我想不明白了。
打日志
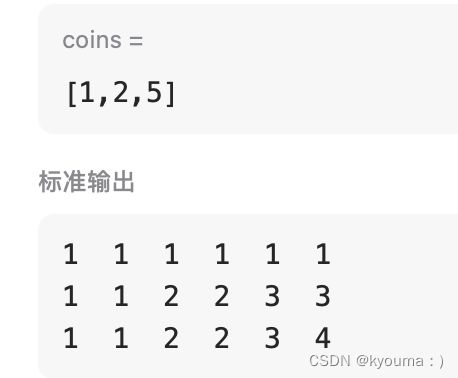
我们看看两种情况的一维dp数组什么样子吧。
先物品再背包:
先背包再物品:
零钱兑换1 和 2的区别
零钱兑换1,问凑出这些amount需要最少的物品数量
零钱兑换2,问凑出这些amount有多少方法(组合)
为什么1就和组合排列没关系,和for循环两层顺序也就没关系呢?
确实在遍历顺序那里,两个 for 循环内外都可以,因为和顺序没关系。
我觉得可能是这样,一个是逻辑上没关系,另者,递推公式是取最小而不是累加,顺序就不会影响取最小这个计算过程。
因为1 1 2 和 2 1 1,对于几种方法的dp数组来说排列的话是2种,组合的话是1张
但如果dp数组记录的是最小硬币数量,对于dp数组来说,记录的都是 3.
对for循环顺序是怎么产生排列 、组合
代码随想录里这段说得很好,很能讲清遍历顺序的不同是怎么出现排列和组合的。

最后dp[s.size()] = 0 即 dp[13] = 0 ,而不是1,因为先用 “apple” 去遍历的时候,dp[8]并没有被赋值为1 (还没用"pen"),所以 dp[13]也不能变成1。
这里和我之前分析排列和组合是怎么产生的很像,因为还没用2,所以和是2的情况只有 1 1,所以和是3的时候,再拿来2也只能出现 1 2 和 111. 如果是排列,用1遍历一遍,也用2遍历了一遍,和是2的情况就有 11 和 2,这样和是3的时候就有 111 21 12 了。
除非是先用 “apple” 遍历一遍,再用 “pen” 遍历,此时 dp[8]已经是1,最后再用 “apple” 去遍历,dp[13]才能是1