优化算法——凸性

优化算法——凸性

---

前言

之前在训练神经网络时，涉及了一些优化算法，如SGD、Adam等，之后将继续深入了解优化算法的原理以及优化算法在深度学习中的重要性。

参考书：
《动手学深度学习》

---

一、优化与深度学习

对于深度学习问题，我们通常会先定义损失函数。一旦我们有了损失函数，我们就可以使用优化算法来尝试最小化损失。在优化中，损失函数通常被称为优化问题的目标函数

1.1. 优化的目标

本质上，优化和深度学习的目标是根本不同的。前者主要关注的是最小化目标，后者则关注在给定有限数据量的情况下寻找合适的模型

例如，训练误差和泛化误差通常不同：

由于优化算法的目标函数通常是基于训练数据集的损失函数，因此优化的目标是减少训练误差。
但是，深度学习的目标是减少泛化误差。为了实现后者，除了使用优化算法来减少训练误差之外，我们还需要注意过拟合。

为了说明上述不同的目标，引入两个概念：风险和经验风险。经验风险是训练数据集的平均损失，而风险则是整个数据群的预期损失

import numpy as np
import torch
from mpl_toolkits import mplot3d
from d2l import torch as d2l


#风险函数f和经验风险函数g
def f(x):
    return x * torch.cos(np.pi * x)

def g(x):
    return f(x) + 0.2 * torch.cos(5 * np.pi * x)


#下图说明，训练数据集的最低经验风险可能与最低风险（泛化误差）不同
def annotate(text,xy,xytext):
    d2l.plt.gca().annotate(text,xy = xy,xytext = xytext,
                           arrowprops = dict(arrowstyle= "->"))
x = torch.arange(0.5,1.5,0.01)
d2l.set_figsize((4.5,3))
d2l.plot(x,[f(x),g(x)],"x","risk")
annotate('min of\nempirical risk', (1.0, -1.2), (0.5, -1.1))
annotate('min of risk', (1.1, -1.05), (0.95, -0.5))
d2l.plt.show()

1.2. 深度学习中的优化挑战

深度学习优化存在许多挑战。其中最令人烦恼的是局部最小值、鞍点和梯度消失。

1.2.1. 局部最小值

对于任何目标函数f(x)，如果在x处对应的f(x)值小于在x附近任意其他点的f(x)值，那么f(x)可能是局部最小值。如果f(x)在x处的值是整个域中目标函数的最小值，那么f(x)是全局最小值。

例如，给定函数

$$f(x)=x\cdot \text{cos}(\pi x)\text{ for }-1.0\le x\le 2.0,$$

我们可以近似该函数的局部最小值和全局最小值。

#局部最小值
x = torch.arange(-1.0, 2.0, 0.01)
d2l.plot(x, [f(x), ], 'x', 'f(x)')
annotate('local minimum', (-0.3, -0.25), (-0.77, -1.0))
annotate('global minimum', (1.1, -0.95), (0.6, 0.8))
d2l.plt.show()

深度学习模型的目标函数通常有许多局部最优解。在这种情况下，小批量上梯度的自然变化能够将参数从局部极小值中跳出。

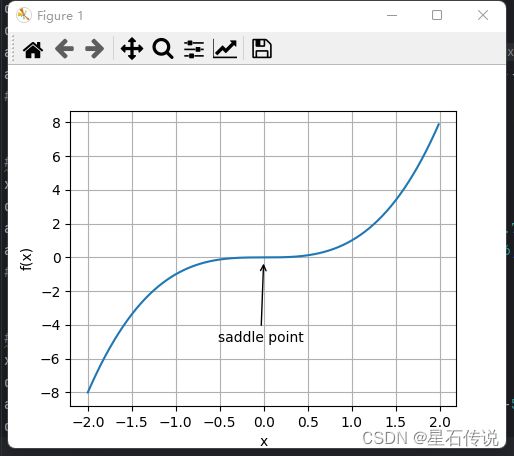
1.2.2. 鞍点

鞍点是梯度消失的另一个原因。鞍点（saddle point）是指函数的所有梯度都消失但既不是全局最小值也不是局部最小值的任何位置。

如图所示：

#鞍点
x = torch.arange(-2.0, 2.0, 0.01)
d2l.plot(x, [x**3], 'x', 'f(x)')
annotate('saddle point', (0, -0.2), (-0.52, -5.0))
d2l.plt.show()

如下图所示，较高维度的鞍点甚至更加隐蔽。考虑这个函数$f(x,y)=x^2-y^2$。它的鞍点为$(0,0)$。这是关于$y$的最大值，也是关于$x$的最小值。此外，它看起来像个马鞍，这就是鞍点的名字由来。

x, y = torch.meshgrid(
    torch.linspace(-1.0, 1.0, 101), torch.linspace(-1.0, 1.0, 101))
z = x**2 - y**2
ax = d2l.plt.figure().add_subplot(111, projection='3d')
ax.plot_wireframe(x, y, z, **{'rstride': 10, 'cstride': 10})
ax.plot([0], [0], [0], 'rx')
ticks = [-1, 0, 1]
d2l.plt.xticks(ticks)
d2l.plt.yticks(ticks)
ax.set_zticks(ticks)
d2l.plt.xlabel('x')
d2l.plt.ylabel('y')
d2l.plt.show()

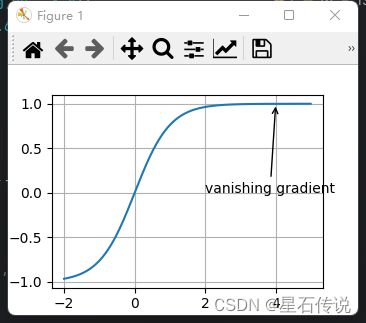
1.2.3. 梯度消失

假设我们想最小化函数f(x)=tanh(x)，然后我们恰好从x=4开始。正如我们所看到的那样，f的梯度接近零。
因此，在我们取得进展之前，优化将会停滞很长一段时间。

x = torch.arange(-2.0, 5.0, 0.01)
d2l.plot(x, [torch.tanh(x)], 'x', 'f(x)')
annotate('vanishing gradient', (4, 1), (2, 0.0))
d2l.plt.show()

​

深度学习的优化充满挑战。幸运的是，有一系列强大的算法表现良好。此外，没有必要找到最优解。局部最优解或其近似解仍然非常有用。

二、凸性

凸性（convexity）在优化算法的设计中起到至关重要的作用， 这主要是由于在这种情况下对算法进行分析和测试要容易。 如果算法在凸性条件设定下的效果很差， 那通常我们很难在其他条件下看到好的结果

2.1. 定义

在进行凸分析之前，我们需要定义凸集（convex sets）和凸函数（convex functions）。

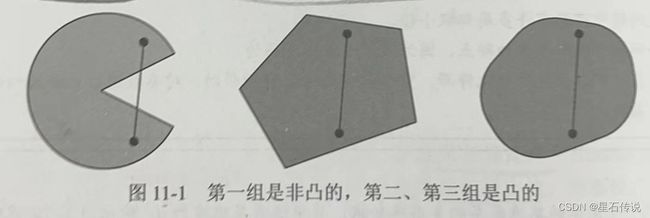
2.1.1. 凸集

凸集（convex set）是凸性的基础。简单地说，如果对于任何$a,b\in \mathcal{X}$，连接$a$和$b$的线段也位于$\mathcal{X}$中，则向量空间中的一个集合$\mathcal{X}$是凸（convex）的。
在数学术语上，这意味着对于所有$\lambda \in [0,1]$，我们得到

$$\lambda a+(1-\lambda )b\in \mathcal{X}\text{ 当 }a,b\in \mathcal{X}.$$

如图所示：

两个凸集的交集是凸的，并集不一定是凸的

2.1.2. 凸函数

现在我们有了凸集，我们可以引入凸函数$f$。 给定一个凸集$\mathcal{X}$，如果对于所有$x,x^{\prime }\in \mathcal{X}$和所有$\lambda \in [0,1]$，函数$f:\mathcal{X}\to \mathbb{R}$是凸的，我们可以得到：

$$\lambda f(x)+(1-\lambda )f(x^{\prime })\ge f(\lambda x+(1-\lambda )x^{\prime }).$$

f = lambda x: 0.5 * x ** 2  # 凸函数
g = lambda x: torch.cos(np.pi * x)  # 非凸函数
h = lambda x: torch.exp(0.5 * x)  # 凸函数
x, segment = torch.arange(-2, 2, 0.01), torch.tensor([-1.5, 1])
d2l.use_svg_display()
_, axes = d2l.plt.subplots(1, 3, figsize=(9, 3))
for ax, func in zip(axes, [f, g, h]):
    d2l.plot([x, segment], [func(x), func(segment)], axes=ax)

d2l.plt.show()

余弦函数为非凸的，而抛物线函数和指数函数为凸的。 请注意，为使该条件有意义， X是凸集的要求是必要的

2.1.3. 詹森不等式

给定一个凸函数$f$，最有用的数学工具之一就是詹森不等式（Jensen’s inequality）。 它是凸性定义的一种推广：

$$\sum _i{\alpha }_{i}f(x_i)\ge f\left(\sum _i{\alpha }_i{x}_i\right)\text{ 并且 }{E}_X[f(X)]\ge f\left(E_X[X]\right),$$

其中${\alpha }_i$是满足${\sum }_i{\alpha }_i=1$的非负实数，$X$是随机变量。
换句话说，凸函数的期望不小于期望的凸函数，其中后者通常是一个更简单的表达式。
詹森不等式的一个常见应用：用一个较简单的表达式约束一个较复杂的表达式。

2.2. 凸函数性质

2.2.1. 局部极小值是全局极小值

这很容易理解，由于凸函数自身的性质可得出

例如，对于凸函数$f(x)=(x-1{)}^2$，有一个局部最小值$x=1$，它也是全局最小值。

f = lambda x: (x - 1) ** 2
d2l.set_figsize()
d2l.plot([x, segment], [f(x), f(segment)], 'x', 'f(x)')
d2l.plt.show()

凸函数的局部极小值同时也是全局极小值这一性质是很方便的。
这意味着如果我们最小化函数，我们就不会“卡住”。
但这并不意味着不能有多个全局最小值，或者可能不存在一个全局最小值。

2.2.2. 凸函数的下水平集是凸的

我们可以方便地通过凸函数的下水平集（below sets）定义凸集。
具体来说，给定一个定义在凸集$\mathcal{X}$上的凸函数$f$，其任意一个下水平集

$${\mathcal{S}}_b:=\{x|x\in \mathcal{X}\text{ and }f(x)\le b\}$$是凸的。

2.2.3. 当且仅当二阶导数>=0时函数是凸的

当一个函数的二阶导数$f:{\mathbb{R}}^n\to \mathbb{R}$存在时，我们很容易检查这个函数的凸性。
我们需要做的就是检查${\nabla }^{2}f⪰0$，
即对于所有$\mathbf{x}\in {\mathbb{R}}^n$，${\mathbf{x}}^{\top }\mathbf{Hx}\ge 0$.
例如，函数$f(\mathbf{x})=\frac{1}{2}\Vert \mathbf{x}{\Vert }^2$是凸的，因为${\nabla }^{2}f=1$，即其导数是单位矩阵。
​
更正式地讲，$f$为凸函数，当且仅当任意二次可微一维函数$f:{\mathbb{R}}^n\to \mathbb{R}$是凸的。
对于任意二次可微多维函数$f:{\mathbb{R}}^n\to \mathbb{R}$，
它是凸的当且仅当它的Hessian${\nabla }^{2}f⪰0$。

2.3. 约束

凸优化的一个很好的特性是能够让我们有效地处理约束（constraints）

即它使我们能够解决以下形式的约束优化问题：

$$\begin{array}{rl}{\mathrm{minimize}}_{\mathbf{x}}& f(\mathbf{x})\\ \text{ subject to }& c_i(\mathbf{x})\le 0\text{ for all }i\in \{1,\dots ,N\}.\end{array}$$

这里$f$是目标函数，$c_i$是约束函数。

2.3.1. 拉格朗日函数

这里我们简略拉格朗日函数$L$的推导，上述推理可以通过以下鞍点优化问题来表示：

$$L(\mathbf{x},{\alpha }_1,\dots ,{\alpha }_n)=f(\mathbf{x})+\sum _{i=1}^n{\alpha }_i{c}_i(\mathbf{x})\text{ 其中 }{\alpha }_i\ge 0.$$

这里的变量${\alpha }_i$（$i=1,\dots ,n$）是所谓的拉格朗日乘数，它确保约束被正确地执行。
选择它们的大小足以确保所有$i$的$c_i(\mathbf{x})\le 0$。

2.3.2. 惩罚

一种至少近似地满足约束优化问题的方法是采用拉格朗日函数$L$。除了满足$c_i(\mathbf{x})\le 0$之外，我们只需将${\alpha }_i{c}_i(\mathbf{x})$添加到目标函数$f(x)$。 这样可以确保不会严重违反约束。

通常，添加惩罚是确保近似满足约束的一种好方法。在实践中，这被证明比精确的满意度更可靠。
此外，对于非凸问题，许多使精确方法在凸情况下的性质（例如，可求最优解）不再成立。

2.3.3. 投影

满足约束条件的另一种策略是投影（projections）。

例如在处理梯度截断时，我们通过

$$\mathbf{g}\leftarrow \mathbf{g}\cdot \min (1,\theta /\Vert \mathbf{g}\Vert ),$$

确保梯度的长度以$\theta$为界限。

这就是$\mathbf{g}$在半径为$\theta$的球上的投影（projection）。
更泛化地说，在凸集$\mathcal{X}$上的投影被定义为

$${\mathrm{Proj}}_{\mathcal{X}}(\mathbf{x})={\mathrm{argmin}}_{{\mathbf{x}}^{\prime }\in \mathcal{X}}\Vert \mathbf{x}-{\mathbf{x}}^{\prime }\Vert .$$

它是$\mathcal{X}$中离$\mathbf{X}$最近的点。

2.4. 小结

• 根据詹森不等式，“一个多变量凸函数的总期望值”大于或等于“用每个变量的期望值计算这个函数的总值“。
• 一个二次可微函数是凸函数，当且仅当其Hessian（二阶导数矩阵）是半正定的（即所有特征值都大于等于零）。
• 凸约束可以通过拉格朗日函数来添加。在实践中，只需在目标函数中加上一个惩罚就可以了。
• 投影映射到凸集中最接近原始点的点。

---

总结

本文首先介绍 了在深度学习中的的一些优化挑战：局部最优解、鞍点问题、梯度消失等；之后，就是着重介绍了凸性，从其定义出发，到它的凸函数性质以及约束条件。为之后的优化算法如梯度下降的学习做准备。

天地有正气，杂然赋流形

–2023-10-19 进阶篇