AVL平衡二叉搜索树
文章目录
-
- 一、二叉搜索树复杂度
- 二、二叉搜索树平衡分析
- 三、改进二叉搜索树
- 四、平衡二叉树
- 五、AVL树特性
-
- 5.1 AVL树的相关概念及特点
- 5.2 普通BST和AVL树添加对比
- 5.3 普通BST添加导致失衡例子
- 六、AVL树设计
-
- 6.1 Node节点定义
- 6.2 构建辅助函数
- 6.3 添加失衡—LL-右旋转(单旋)
- 6.4 添加失衡—RR-左旋转(单旋)
- 6.5 添加失衡—LR(双旋)
- 6.6 添加失衡—RL(双旋)
- 6.7 删除失衡
- 七、JAVA编码实现AVL树
- 八、总结
-
- 8.1 添加
- 8.2 删除
- 8.3平均时间复杂度
- 九、参考文献

一、二叉搜索树复杂度
二叉树相关的知识可以通过前置文章二叉搜索树学习。我们可以知道BST的添加、删除和搜索效率都非常的高,其复杂度与元素的个数没有关系,只与树的高度有关系,即复杂度为:O(h) ,h为树的高度,当BST为满二叉树时,其复杂度为O(logn),n为元素个数,此时:O(h) == O(logn)。
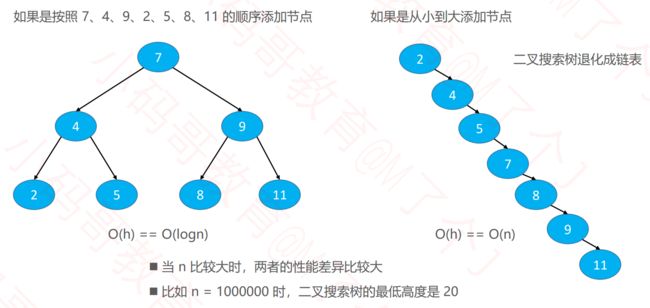
但是如果是按照从小到大的顺序添加结点,如上图右边所示,可以看到这样的BST与链表是一样的,其复杂度O(h) = O(n)我们称这样的BST退化成了链表。
以上两种BST的的效率有巨大的差距,当n = 1000000(一百万)时,左边的BST最坏情况下只需要进行20次查找,右边的BST最坏情况下需要进行一百万次查找

除了添加元素可能会让BST退化成链表之外,删除也有可能会让BST退化成链表。如下图所示,当树的高度足够大时,也面临着上面的问题。
二、二叉搜索树平衡分析
有什么办法能够解决上面的问题呢?当我们的二叉树更加平衡时,就可以解决上面的问题,所谓的平衡就是当节点数量固定时,左右子树的高度越接近,这棵二叉树就越平衡(高度越低),如下图所示:
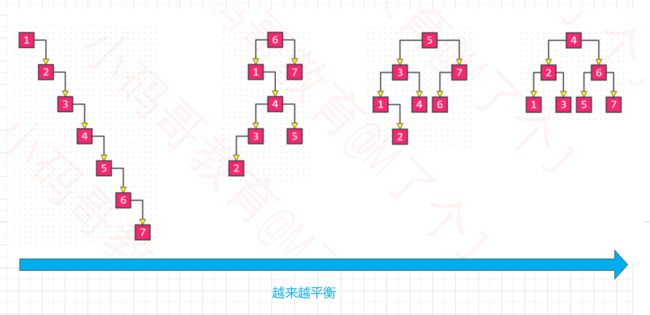
最理想的平衡,就是像完全二叉树、满二叉树那样,高度是最小的

三、改进二叉搜索树
首先我们需要知道:
- 首先,节点的添加、删除顺序是无法限制的,可以认为是随机的
- 所以,改进方案是:在节点的添加、删除操作之后,想办法让二叉搜索树恢复平衡(减小树的高度)
举个栗子,我们将下图中左边的BST调整为右边的BST:

可以看到这样的调整让BST的高度减少了1,并且没有改变BST的性质,这就是一种有效调整。那右边的BST可以继续调整吗?其实可以继续调整的,但是没有必要,因为如果接着继续调整节点的位置,会做过多的运算,这样的话付出的代价可能会比较大。
所以我们的做法是:用尽量少的调整次数达到适度平衡即可。
一棵达到适度平衡的二叉搜索树,可以称之为:平衡二叉搜索树
四、平衡二叉树
所谓平衡二叉树是指树中任一结点的左、右子树高度大致相同。经典的BBST有:
- AVL树(Windows NT 内核中广泛使用)
- 红黑树(红黑树的应用十分广泛,例如C++ STL库中的map、set;Java 的 TreeMap、TreeSet、HashMap、HashSet;Linux 的进程调度;Nginx 的 timer 管理)
一般也称它们为:自平衡的二叉搜索树(Self-balancing Binary Search Tree)
五、AVL树特性
5.1 AVL树的相关概念及特点
AVL树定义如下:是平衡二叉树或者是一棵空树,或者是具有以下性质的二叉排序树:
- 每个节点的平衡因子只可能是 1、0、-1(绝对值 ≤ 1,如果超过 1,称之为“失衡”)
- 每个节点的左右子树高度差不超过 1
- 因为每个结点的高度差不超过1,所以AVL树搜索、添加、删除的时间复杂度是 O(logn)

平衡因子(Balance Factor):某结点的左右子树的高度差,即左子树高度减去右子树高度
5.2 普通BST和AVL树添加对比
我们往一棵普通的BST和一棵AVL树中添加同一组结点:35, 37, 34, 56, 25, 62, 57, 9, 74, 32, 94, 80, 75, 100, 16, 82
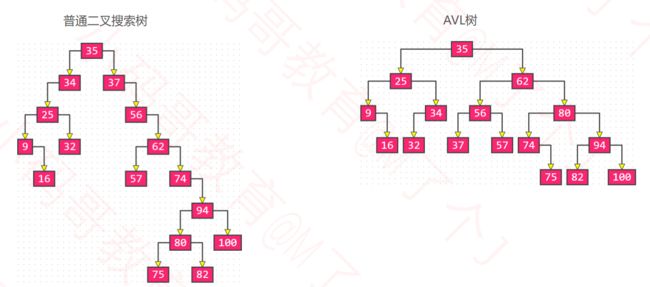
5.3 普通BST添加导致失衡例子
往下面的BST中添加13这个元素(注意下面的BST并不完整,只是其中的一部分)
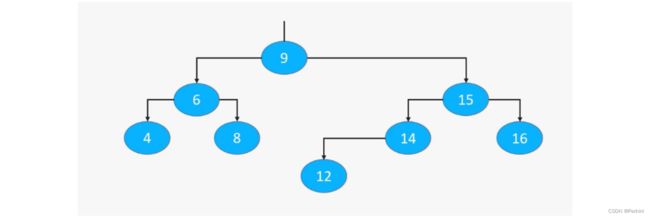
可以看到在添加13这个元素前,图片里的树是平衡的,因为任意结点的平衡因子都小于1,但是当我们添加13这个结点后,这棵树就会变成以下这样:
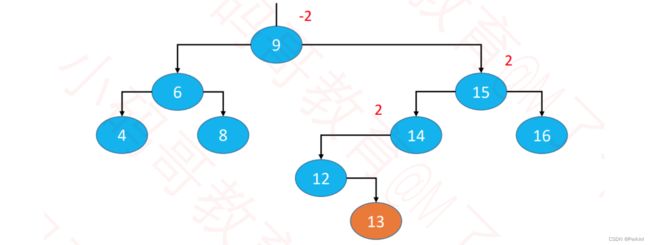
可以看到当添加了元素之后,有三个结点处于不平衡的状态了,并且对于整棵二叉树有:
- 最坏情况:可能会导致所有祖先节点都失衡
- 父节点、非祖先节点,都不可能失衡
六、AVL树设计
6.1 Node节点定义
public class AVLTree<K extends Comparable<K>, V> {
private class Node{
public K key;
public V value;
public Node left, right;
public int height;
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
height = 1;
}
}
private Node root;
private int size;
public AVLTree(){
root = null;
size = 0;
}
}
6.2 构建辅助函数
-
节点高度:左右孩子的节点高度可快速计算节点的平衡因子。
/** * 获得节点node的高度 * @param node 节点Node * @return */ private int getHeight(Node node){ if(node == null) return 0; return node.height; } -
平衡因子计算:用于快速计算左右孩子节点高度差。
/** * 获得节点node的平衡因子 * @param node 节点Node * @return */ private int getBalanceFactor(Node node){ if(node == null) return 0; return getHeight(node.left) - getHeight(node.right); } -
是否为二叉树:重新构建二叉树后确保是否满足二叉树特性
/** * 判断该二叉树是否是一棵二分搜索树 * @return */ public boolean isBST(){ ArrayList<K> keys = new ArrayList<>(); // 利用中序遍历的有序性 inOrder(root, keys); for(int i = 1 ; i < keys.size() ; i ++) if(keys.get(i - 1).compareTo(keys.get(i)) > 0) return false; return true; } private void inOrder(Node node, ArrayList<K> keys){ if(node == null) return; inOrder(node.left, keys); keys.add(node.key); inOrder(node.right, keys); } -
是否平衡二叉树:重新构建二叉树后确保是否满足平衡二叉树特性。
/** * 判断该二叉树是否是一棵平衡二叉树 * @return */ public boolean isBalanced(){ // 判断以Node为根的二叉树是否是一棵平衡二叉树,递归算法 return isBalanced(root); } private boolean isBalanced(Node node){ if(node == null) return true; int balanceFactor = getBalanceFactor(node); if(Math.abs(balanceFactor) > 1) return false; return isBalanced(node.left) && isBalanced(node.right); }
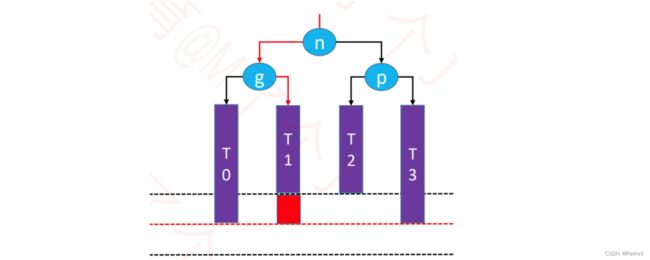
6.3 添加失衡—LL-右旋转(单旋)
在图中展示的二叉树里n表示node,p表示parent、g表示grandparent。这棵本来是平衡的(看下面的辅助线),但是因为n结点添加了一个元素,现在导致g结点现在不平衡了。
g结点不平衡,是因为g结点的左子树的左侧子树(LL)让其不平衡,所以我们称旋转的方式为:LL-右旋转

/**
* 对节点y进行向右旋转操作,返回旋转后新的根节点x
*
* y x
* / \ / \
* x T4 向右旋转 (y) z y
* / \ - - - - - - - -> / \ / \
* z T3 T1 T2 T3 T4
* / \
* T1 T2
*
*
* @param y
* @return
*/
private Node rightRotate(Node y) {
Node x = y.left;
Node T3 = x.right;
// 向右旋转过程
x.right = y;
y.left = T3;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
旋转后如下:
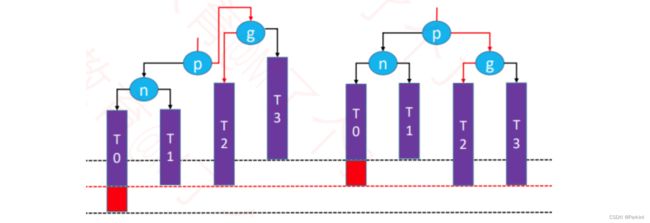
调整后的二叉树仍然是一棵二叉搜索树,依然保持:T0 < n < T1 < p < T2 < g < T3
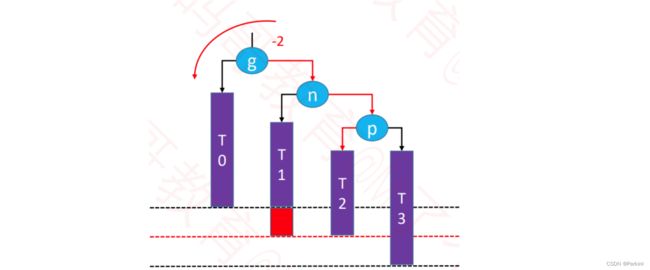
6.4 添加失衡—RR-左旋转(单旋)
下面这种情况的失衡,由于失衡结点g的右子树的右子树(RR)增加了一个结点,所以我们需要让g左旋转来维持平衡
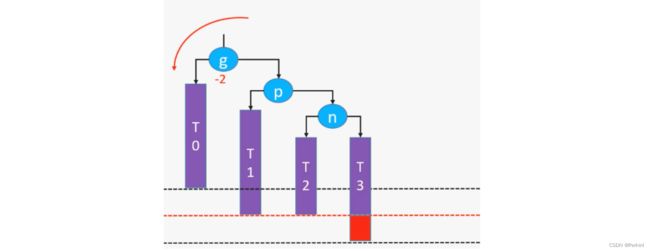
g结点不平衡,是因为g结点的右子树的右侧子树(RR)让其不平衡,所以我们称旋转的方式为:RR-左旋转
/**
* 对节点y进行向左旋转操作,返回旋转后新的根节点x
*
* y x
* / \ / \
* T1 x 向左旋转 (y) y z
* / \ - - - - - - - -> / \ / \
* T2 z T1 T2 T3 T4
* / \
* T3 T4
*
* @param y
* @return
*/
private Node leftRotate(Node y) {
Node x = y.right;
Node T2 = x.left;
// 向左旋转过程
x.left = y;
y.right = T2;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
旋转后如下:
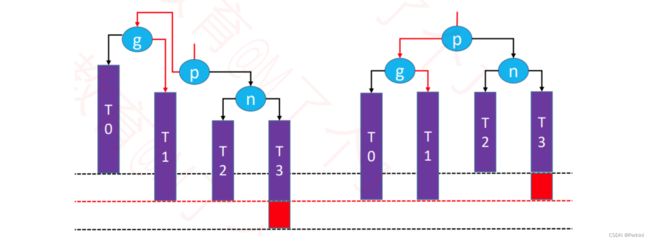
调整后的二叉树仍然是一棵二叉搜索树,依然保持:T0 < n < T1 < p < T2 < g < T3
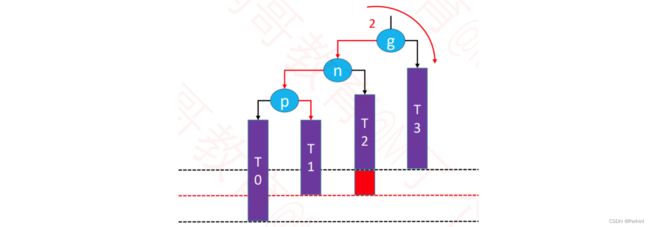
6.5 添加失衡—LR(双旋)
下面失去平衡的例子,结点g的左子树的右子树(LR)增加了一个结点,从而使g失去了平衡。
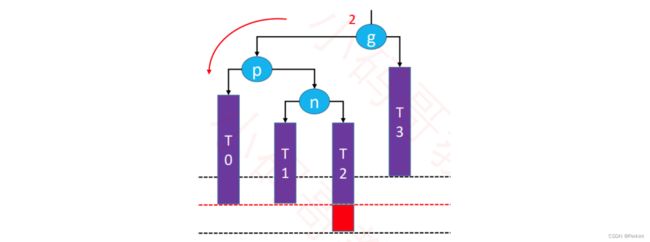
我们的处理的办法是先左旋转(右侧)让失去平衡的节点都移动到左侧后在进行左旋转(左侧)从而使这棵树达到平衡,所以我们称旋转的方式为:LR-右旋转左旋转(双旋)
-
先让结点
P左旋转,让n成为父结点p.right = n.left n.left = p -
现在又回到
g左子树的左子树(T0结点)不平衡的情况了,这种我们需要LL-右旋转,这里对g进行右旋转。让n成为根节点。g.left = n.right n.right = g
// 合并后的代码
if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
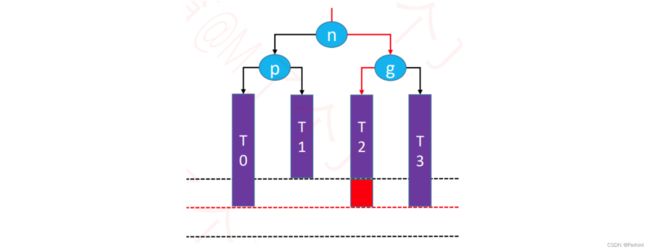
6.6 添加失衡—RL(双旋)
下面失去平衡的例子,结点g的右子树的左子树(RL)增加了一个结点,从而使g失去了平衡。

-
我们需要先对
p结点进行LL-右旋转,让n变为根结点p.left = n.right n.right = p -
现在只需要将
g进行RR左旋转,让n成为根节点。即可让整棵二叉树恢复平衡g.right = n.left n.left = g
// 合并后的代码
if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
6.7 删除失衡
除了添加结点可能会导致失衡,删除结点也同样会导致树失去平衡,例如我们现在要删除下面的结点16
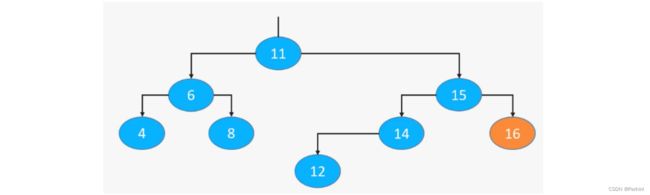
我们可以看到结点16被删除后整个二叉树会变成下图中的情况,很显然结点15的平衡因子为2,失去了平衡:

其实看到上面失衡的情况,我们可以快速的发现,这种失衡可以通过LL-右旋转来解决,这种不是和添加结点失衡一样吗?但真的是一样的吗?我们看下面的例子将失衡结点进行右旋

我们会发现在右边的树虽然达到了平衡的效果,但是整体的高度减少了1,整体高度减少了就有可能会导致其父结点失去平衡。
- 如果绿色节点不存在,更高层的祖先节点可能也会失衡,需要再次恢复平衡,然后又可能导致更高层的祖先节点失衡
- 极端情况下,所有祖先节点都需要进行恢复平衡的操作,共 O(logn) 次调整
同样的,我们删除元素导致失衡也有LL、RR、LR-RR、RL-LL几种情况,和添加结点导致的失衡是一样的处理方式
七、JAVA编码实现AVL树
实现一个可以存储K,V格式数据的一个AVL平衡二叉树
public class AVLTree<K extends Comparable<K>, V> {
private class Node {
public K key;
public V value;
public Node left, right;
public int height;
public Node(K key, V value) {
this.key = key;
this.value = value;
left = null;
right = null;
height = 1;
}
}
private Node root;
private int size;
public AVLTree() {
root = null;
size = 0;
}
public int getSize() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
/**
* 判断该二叉树是否是一棵二分搜索树
*
* @return
*/
public boolean isBST() {
ArrayList<K> keys = new ArrayList<>();
// 利用中序遍历的有序性
inOrder(root, keys);
for (int i = 1; i < keys.size(); i++)
if (keys.get(i - 1).compareTo(keys.get(i)) > 0)
return false;
return true;
}
/**
* 中序遍历
* @param node 节点
* @param keys 维护数据的集合
*/
private void inOrder(Node node, ArrayList<K> keys) {
if (node == null)
return;
inOrder(node.left, keys);
keys.add(node.key);
inOrder(node.right, keys);
}
/**
* 判断该二叉树是否是一棵平衡二叉树
*
* @return
*/
public boolean isBalanced() {
// 判断以Node为根的二叉树是否是一棵平衡二叉树,递归算法
return isBalanced(root);
}
private boolean isBalanced(Node node) {
if (node == null)
return true;
int balanceFactor = getBalanceFactor(node);
if (Math.abs(balanceFactor) > 1)
return false;
return isBalanced(node.left) && isBalanced(node.right);
}
/**
* 获得节点node的高度
*
* @param node 节点Node
* @return
*/
private int getHeight(Node node) {
if (node == null)
return 0;
return node.height;
}
/**
* 获得节点node的平衡因子
*
* @param node 节点Node
* @return
*/
private int getBalanceFactor(Node node) {
if (node == null)
return 0;
return getHeight(node.left) - getHeight(node.right);
}
/**
* 对节点y进行向右旋转操作,返回旋转后新的根节点x
*
* y x
* / \ / \
* x T4 向右旋转 (y) z y
* / \ - - - - - - - -> / \ / \
* z T3 T1 T2 T3 T4
* / \
* T1 T2
*
*
* @param y
* @return
*/
private Node rightRotate(Node y) {
Node x = y.left;
Node T3 = x.right;
// 向右旋转过程
x.right = y;
y.left = T3;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
/**
* 对节点y进行向左旋转操作,返回旋转后新的根节点x
*
* y x
* / \ / \
* T1 x 向左旋转 (y) y z
* / \ - - - - - - - -> / \ / \
* T2 z T1 T2 T3 T4
* / \
* T3 T4
*
* @param y
* @return
*/
private Node leftRotate(Node y) {
Node x = y.right;
Node T2 = x.left;
// 向左旋转过程
x.left = y;
y.right = T2;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
/**
* 向二分搜索树中添加新的元素(key, value)
* @param key key
* @param value value
*/
public void add(K key, V value) {
// 向以node为根的二分搜索树中插入元素(key, value),递归算法
root = add(root, key, value);
}
private Node add(Node node, K key, V value) {
if (node == null) {
size++;
return new Node(key, value);
}
if (key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if (key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
// 更新height
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
// 计算平衡因子
int balanceFactor = getBalanceFactor(node);
/* 平衡维护 */
// LL
if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0)
return rightRotate(node);
// RR
if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0)
return leftRotate(node);
// LR
if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
// RL
if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
/**
* 返回以node为根节点的二分搜索树中,key所在的节点
* @param node 节点
* @param key key
* @return
*/
private Node getNode(Node node, K key) {
if (node == null)
return null;
if (key.equals(node.key))
return node;
else if (key.compareTo(node.key) < 0)
return getNode(node.left, key);
else // if(key.compareTo(node.key) > 0)
return getNode(node.right, key);
}
/**
* 判断是否包含key
* @param key key
* @return
*/
public boolean contains(K key) {
return getNode(root, key) != null;
}
/**
* 获取key的value
* @param key key
* @return
*/
public V get(K key) {
Node node = getNode(root, key);
return node == null ? null : node.value;
}
/**
* 修改key的值为 newValue
* @param key key
* @param newValue newValue
*/
public void set(K key, V newValue) {
Node node = getNode(root, key);
if (node == null)
throw new IllegalArgumentException(key + " doesn't exist!");
node.value = newValue;
}
/**
* 返回以node为根的二分搜索树的最小值所在的节点
* @param node 节点Node
* @return
*/
private Node minimum(Node node) {
if (node.left == null)
return node;
return minimum(node.left);
}
/**
* 从二分搜索树中删除键为key的节点
* @param key key
* @return
*/
public V remove(K key) {
Node node = getNode(root, key);
if (node != null) {
root = remove(root, key);
return node.value;
}
return null;
}
private Node remove(Node node, K key) {
if (node == null)
return null;
Node retNode;
if (key.compareTo(node.key) < 0) {
node.left = remove(node.left, key);
// return node;
retNode = node;
} else if (key.compareTo(node.key) > 0) {
node.right = remove(node.right, key);
// return node;
retNode = node;
} else { // key.compareTo(node.key) == 0
if (node.left == null) { // 待删除节点左子树为空的情况
Node rightNode = node.right;
node.right = null;
size--;
// return rightNode;
retNode = rightNode;
} else if (node.right == null) { // 待删除节点右子树为空的情况
Node leftNode = node.left;
node.left = null;
size--;
// return leftNode;
retNode = leftNode;
} else { // 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
//successor.right = removeMin(node.right); TODO 特别注意
successor.right = remove(node.right, successor.key);
successor.left = node.left;
node.left = node.right = null;
// return successor;
retNode = successor;
}
}
if (retNode == null)
return null;
// 更新height
retNode.height = 1 + Math.max(getHeight(retNode.left), getHeight(retNode.right));
// 计算平衡因子
int balanceFactor = getBalanceFactor(retNode);
/* 平衡维护 */
// LL
if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0)
return rightRotate(retNode);
// RR
if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0)
return leftRotate(retNode);
// LR
if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
retNode.left = leftRotate(retNode.left);
return rightRotate(retNode);
}
// RL
if (balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
retNode.right = rightRotate(retNode.right);
return leftRotate(retNode);
}
return retNode;
}
}
八、总结
8.1 添加
- 可能会导致所有祖先节点都失衡;
- 只要让高度最低的失衡节点恢复平衡,整棵树就恢复平衡【仅需要O(1)次调整】
8.2 删除
- 可能会导致父节点或祖先节点失衡(只有一个节点会失衡)
- 恢复平衡后,可能会导致更高层的祖先节点失衡【最多需要O(logn)次调整】
8.3平均时间复杂度
- 搜索:O(logn)
- 添加:O(logn),仅需要O(1)次的旋转操作
- 删除:O(logn),最多需要O(logn)次的旋转操作
九、参考文献
- https://blog.csdn.net/fengxiandada/article/details/124046346
- 源代码地址
关注公众号 ,专注于java大数据领域离线、实时技术干货定期分享!如有问题随时沟通交流! www.lllpan.top
![]()