平衡二叉树-插入、删除(java代码)
二叉树定义
目录
一、概念
1、定义
2、平衡因子
3、最小不平衡子树
二、旋转纠正
1、旋转方式
2、旋转纠正类型
LL型
LR型
RR型
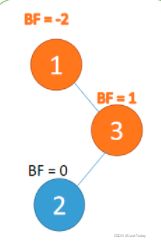
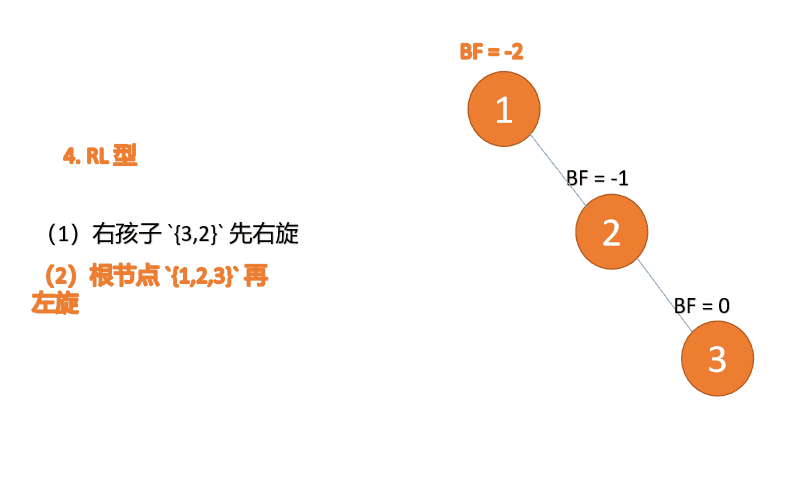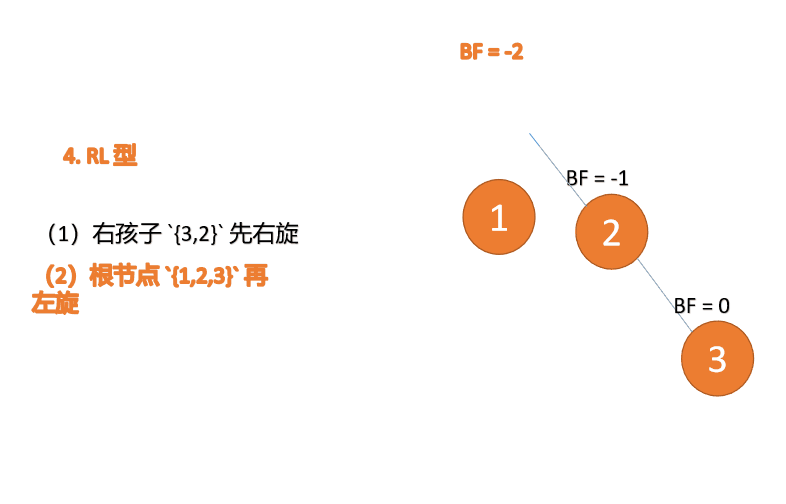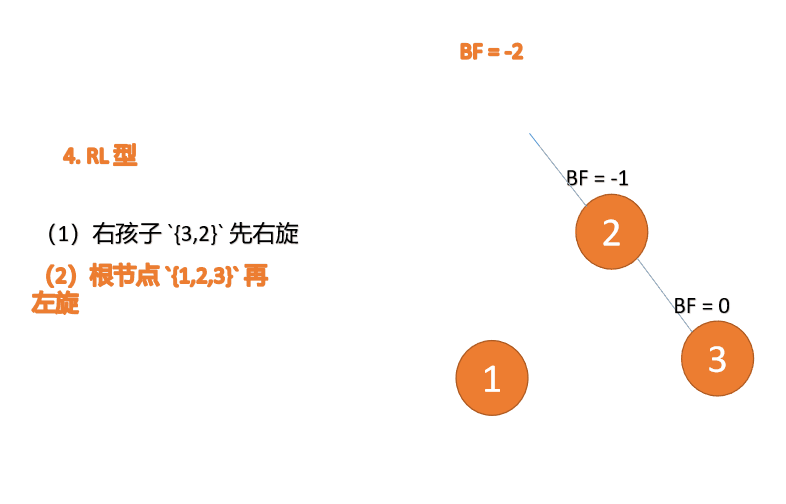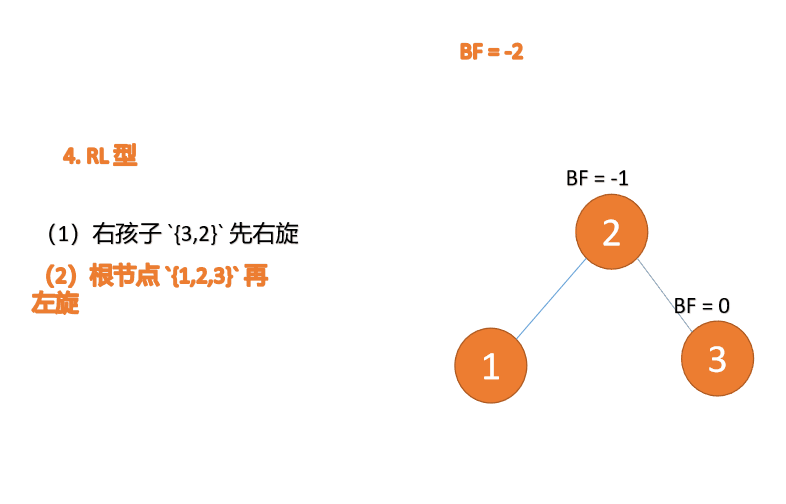
RL型
三、插入
四、删除
五、完整代码实现
一、概念
1、定义
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树
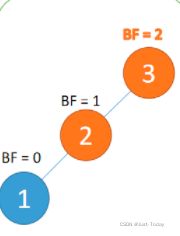
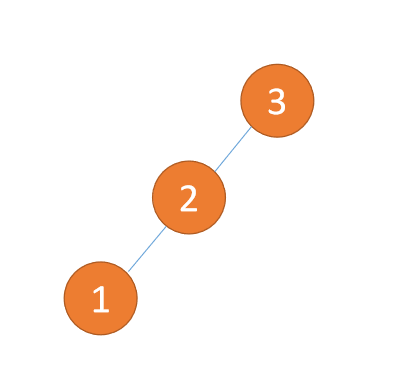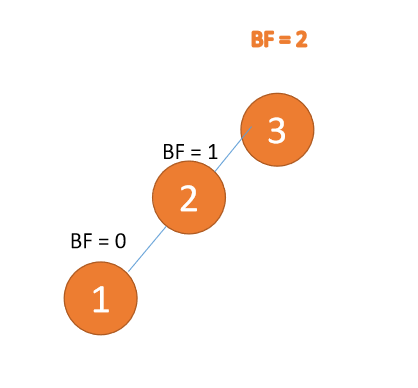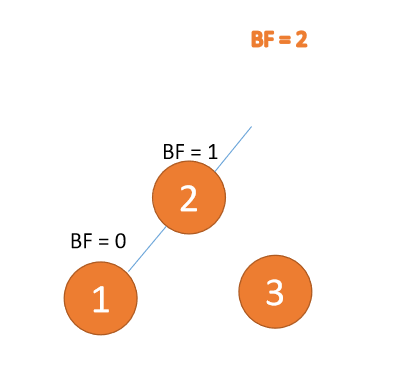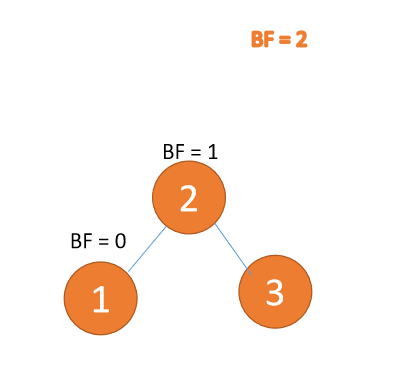
2、平衡因子
定义:左子树和右子树高度差
计算:左子树高度 - 右子树高度的值
别名:简称 BF(Balance Factor)
一般来说 BF 的绝对值大于 1,,平衡树二叉树就失衡,需要「旋转」纠正
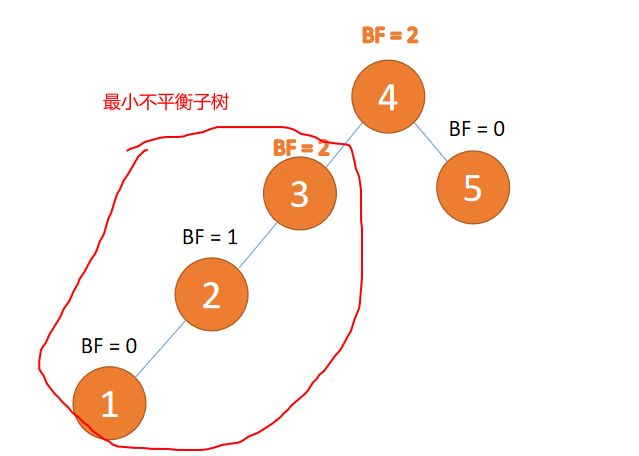
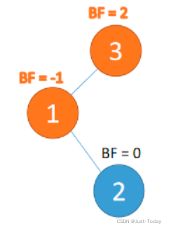
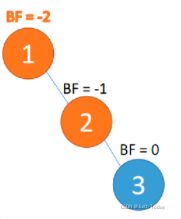
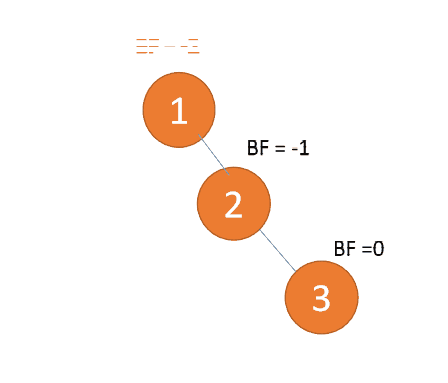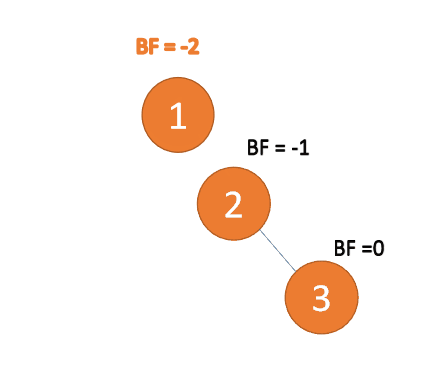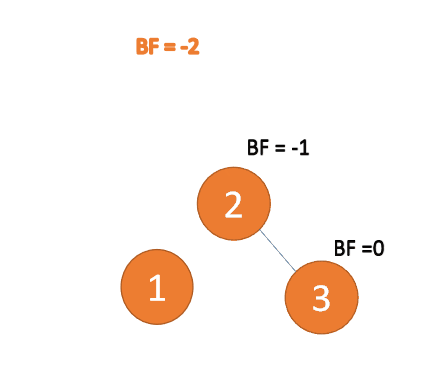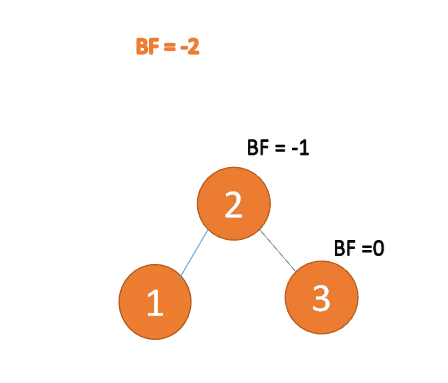
3、最小不平衡子树
距离插入节点最近的,并且 BF 的绝对值大于 1 的节点为根节点的子树。
「旋转」纠正只需要纠正「最小不平衡子树」即可
二、旋转纠正
1、旋转方式
- 左旋
- 旧根节点为新根节点的左子树
- 新根节点的左子树(如果存在)为旧根节点的右子树
![]()
- 右旋:
- 旧根节点为新根节点的右子树
- 新根节点的右子树(如果存在)为旧根节点的左子树
![]()
2、旋转纠正类型
LL型
插入左孩子的左子树,右旋
代码实现
/**
* LL型旋转
* @param current
* @param parent
*/
public void rotateLL(AVLTreeNode current, AVLTreeNode parent) {
AVLTreeNode left = current.getLeft();
current.setLeft(left.getRight());
left.setRight(current);
if(parent != null){
if(parent.getLeft() == current){
parent.setLeft(left);
}else{
parent.setRight(left);
}
}else{
root = left;
}
//更新高度
current.setHeight(Math.max(getHeight(current.getLeft()), getHeight(current.getRight())) + 1);
left.setHeight(Math.max(getHeight(left.getLeft()), current.getHeight()) + 1);
}LR型
插入左孩子的右子树,先左旋,再右旋
代码实现
/**
* LR型旋转
* @param current
* @param parent
*/
public void rotateLR(AVLTreeNode current, AVLTreeNode parent) {
AVLTreeNode left = current.getLeft();
AVLTreeNode lefeRightNode = left.getRight();
left.setRight(lefeRightNode.getLeft());
lefeRightNode.setLeft(left);
current.setLeft(lefeRightNode.getRight());
lefeRightNode.setRight(current);
if(parent != null){
if(parent.getLeft() == current){
parent.setLeft(lefeRightNode);
}else{
parent.setRight(lefeRightNode);
}
}else{
root = lefeRightNode;
}
//更新高度
left.setHeight(Math.max(getHeight(left.getLeft()), getHeight(left.getRight())) + 1);
current.setHeight(Math.max(getHeight(current.getLeft()), getHeight(current.getRight())) + 1);
lefeRightNode.setHeight(Math.max(left.getHeight(), current.getHeight()) + 1);
}RR型
插入右孩子的右子树,左旋
代码实现
/**
* RR型旋转
* @param current
* @param parent
*/
public void rotateRR(AVLTreeNode current, AVLTreeNode parent) {
AVLTreeNode right = current.getRight();
current.setRight(right.getLeft());
right.setLeft(current);
if(parent != null){
if(parent.getLeft() == current){
parent.setLeft(right);
}else{
parent.setRight(right);
}
}else{
root = right;
}
//更新高度
current.setHeight(Math.max(getHeight(current.getLeft()), getHeight(current.getRight())) + 1);
right.setHeight(Math.max(current.getHeight(), getHeight(right.getRight())) + 1);
}RL型
插入右孩子的左子树,先右旋,再左旋
代码实现
/**
* RL型旋转
* @param current
* @param parent
*/
public void rotateRL(AVLTreeNode current, AVLTreeNode parent) {
AVLTreeNode right = current.getRight();
AVLTreeNode rightLeft = right.getLeft();
right.setLeft(rightLeft.getRight());
rightLeft.setRight(right);
current.setRight(rightLeft.getLeft());
rightLeft.setLeft(current);
if(parent != null){
if(parent.getLeft() == current){
parent.setLeft(rightLeft);
}else{
parent.setRight(rightLeft);
}
}else{
root = rightLeft;
}
//更新高度
right.setHeight(Math.max(getHeight(right.getLeft()), getHeight(right.getRight())) + 1);
current.setHeight(Math.max(getHeight(current.getLeft()), getHeight(current.getRight())) + 1);
rightLeft.setHeight(Math.max(current.getHeight(), right.getHeight()) + 1);
}三、插入
基本思路:在找到需要插入的位置的同时,还需要使用栈存储记录到达插入位置所经过的节点,在完成插入之后,之后依次弹栈,依次检查弹出的节点平衡因子是否符合平衡二叉树的要求。
代码实现
//插入节点
public AVLTreeNode insertTreeNode(int data){
if(root == null){
//根节点为空
root = new AVLTreeNode(data);
return root;
}else{
//用栈保存遍历的节点位置,后续依次弹出对节点进行旋转调整以保持二叉树的平衡
Stack stack = new Stack<>();
//判断是插入左右位置
boolean isLeft = false;
AVLTreeNode current = root;
AVLTreeNode parent = null;
while(current != null){
stack.push(current);
parent = current;
if(current.getData() > data){
current = current.getLeft();
isLeft = true;
}else{
current = current.getRight();
isLeft = false;
}
}
//循环结束则说明找到插入位置
AVLTreeNode node = new AVLTreeNode(data);
if(isLeft){
parent.setLeft(node);
}else{
parent.setRight(node);
}
//对遍历的节点进行旋转调整
while(!stack.isEmpty()){
current = stack.pop();
if(stack.isEmpty()){
parent = null;
}else{
parent = stack.peek();
}
//对节点进行旋转调整
rotate(current, parent);
}
return node;
}
} /**
* 对指定结点进行调整
* @param current
* @param parent
*/
public void rotate(AVLTreeNode current, AVLTreeNode parent) {
//在判断平衡因子之前,先对当前结点更新高度
current.setHeight(Math.max(getHeight(current.getLeft()), getHeight(current.getRight())) + 1);
//得到该节点的平衡因子
int balanceFactor = getbalance(current);
//对于LL和LR型旋转,只要不是LL型,其他的都可以看做是LR型
//在这里是为了防止发生:结点的平衡因子是2,其孩子结点的平衡因子出现0的情况
//RR与RL也是类似的
if(balanceFactor == 2){
//左子树
if(getbalance(current.getLeft()) == 1){
//LL
rotateLL(current, parent);
}else{
//LR
rotateLR(current, parent);
}
}else if(balanceFactor == -2){
//右子树
if(getbalance(current.getRight()) == -1){
//RR
rotateRR(current, parent);
}else{
//RL
rotateRL(current, parent);
}
}
}四、删除
基本思路:首先也是需要找到所要删除的结点,在这个过程中,同样需要使用栈保存所经过的结点。完成删除后,依次弹栈,对不平衡的二叉树进行调整。
在这里有种特殊情况:当删除的结点的左右子树都存在时,那么需要找到删除结点的最小中序后继结点,并将其代替删除结点的位置,并将最小中序后继结点删除。这个过程是在删除结点的右子树上进行的,那么就有可能会造成该右子树的不平衡;所以,在找最小中序后继的时候,同样需要保存所经过的结点,完成最小后继结点的删除之后,对该右子树进行调整,使其成为平衡二叉子树。
代码实现
/**
* 删除节点
* @param data
* @return
*/
public AVLTreeNode deleteNode(int data){
if(root == null){
return null;
}else{
//保存遍历节点,以后续对节点进行旋转调整
Stack stack = new Stack<>();
AVLTreeNode current = root;
AVLTreeNode parent = null;
boolean isLeft = false;
while(current != null && current.getData() != data){
stack.push(current);
parent = current;
if(current.getData() > data){
current = current.getLeft();
isLeft = true;
}else{
current = current.getRight();
isLeft = false;
}
}
if(current == null){
//找不到对应节点
return null;
}else{
if(current.getLeft() != null && current.getRight() != null){
//存在左右子树
//找到最小中序后继
AVLTreeNode minNode = finMinInNode(current);
minNode.setLeft(current.getLeft());
minNode.setRight(current.getRight());
if(parent == null){
root = minNode;
}else{
if(isLeft){
parent.setLeft(minNode);
}else{
parent.setRight(minNode);
}
//对替换的节点进行旋转调整
rotate(minNode, parent);
}
}else if(current.getLeft() != null){
//存在左子树
if(parent == null){
root = current.getLeft();
}else{
if(isLeft){
parent.setLeft(current.getLeft());
}else{
parent.setRight(current.getLeft());
}
}
}else if(current.getRight() != null){
//存在右子树
if(parent == null){
root = current.getRight();
}else{
if(isLeft){
parent.setLeft(current.getRight());
}else{
parent.setRight(current.getRight());
}
}
}else{
//叶子节点
if(parent == null){
root = null;
return current;
}else{
if(isLeft){
parent.setLeft(null);
}else{
parent.setRight(null);
}
}
}
//平衡遍历节点
if(stack.isEmpty()){
//删除的是根节点
//平衡替换的节点
rotate(root, parent);
}else{
while(!stack.isEmpty()){
AVLTreeNode pop = stack.pop();
if(!stack.isEmpty()){
parent = stack.peek();
}else{
parent = null;
}
rotate(pop, parent);
}
}
return current;
}
}
} 找到最小中序后继
/**
* 找到最小中序后继
* 若找到对应节点,删除该节点,找的过程保存遍历的节点,找到对各个节点进行旋转调整保持平衡
* @param current
* @return
*/
public AVLTreeNode finMinInNode(AVLTreeNode current) {
//保存遍历节点
Stack stack = new Stack<>();
AVLTreeNode node = current.getRight();
AVLTreeNode preNode = current;
//一直向左遍历
while(node.getLeft() != null){
stack.push(node);
preNode = node;
node = node.getLeft();
}
if(node == current.getRight()){
//当前节点的最小中序后继节点是该节点的右节点,不需要进行调整
current.setRight(node.getRight());
}else{
preNode.setLeft(node.getRight());
while(!stack.isEmpty()){
AVLTreeNode pop = stack.pop();
if(stack.isEmpty()){
preNode = current;
}else{
preNode = stack.peek();
}
rotate(pop, preNode);
}
}
return node;
} 五、完整代码实现
package com.mzp.tree;
/**
* 平衡二叉树节点
*/
public class AVLTreeNode {
private int data;
//高度
private int height;
//左子节点
private AVLTreeNode left;
//右子节点
private AVLTreeNode right;
public AVLTreeNode(int data) {
this.data = data;
this.height = 1;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public int getHeight() {
return height;
}
public void setHeight(int height) {
this.height = height;
}
public AVLTreeNode getLeft() {
return left;
}
public void setLeft(AVLTreeNode left) {
this.left = left;
}
public AVLTreeNode getRight() {
return right;
}
public void setRight(AVLTreeNode right) {
this.right = right;
}
}
package com.mzp.tree;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
public class AVLTree {
private AVLTreeNode root;
public static void main(String[] args) {
AVLTree tree = new AVLTree();
//4 2 1 测试LL型旋转 最小不平衡二叉树为整颗树
/*tree.insertTreeNode(4);
tree.insertTreeNode(2);
tree.insertTreeNode(1);*/
//6 4 8 2 1 测试LL型旋转 最小不平衡二叉树是一般的树
/*tree.insertTreeNode(6);
tree.insertTreeNode(4);
tree.insertTreeNode(8);
tree.insertTreeNode(2);
tree.insertTreeNode(1);*/
// 测试RR型调整
// 4 6 7
/*tree.insertTreeNode(4);
tree.insertTreeNode(6);
tree.insertTreeNode(7);*/
// 4 2 6 7 8
/*tree.insertTreeNode(4);
tree.insertTreeNode(2);
tree.insertTreeNode(6);
tree.insertTreeNode(7);
tree.insertTreeNode(8);*/
// 测试LR型旋转
// 4 2 3
/*tree.insertTreeNode(4);
tree.insertTreeNode(2);
tree.insertTreeNode(3);*/
// 5 6 4 2 3
/*tree.insertTreeNode(5);
tree.insertTreeNode(6);
tree.insertTreeNode(4);
tree.insertTreeNode(2);
tree.insertTreeNode(3);*/
// 测试RL型旋转
// 5 7 6
tree.insertTreeNode(5);
tree.insertTreeNode(7);
tree.insertTreeNode(6);
// 4 2 5 7 6
/*tree.insertTreeNode(4);
tree.insertTreeNode(2);
tree.insertTreeNode(5);
tree.insertTreeNode(7);
tree.insertTreeNode(6);*/
//删除
/*tree.deleteNode(7);
tree.deleteNode(5);
tree.deleteNode(2);
//tree.deleteNode(6);*/
tree.deleteNode(6);
/*tree.deleteNode(8);
tree.deleteNode(2);*/
System.out.println("层级遍历");
tree.levelTraversal(tree.root);
System.out.println();
System.out.println("前序遍历");
tree.preTraversal(tree.root);
System.out.println();
System.out.println("中序遍历");
tree.inTraversal(tree.root);
System.out.println();
System.out.println("后序遍历");
tree.postTraversal(tree.root);
}
//层级遍历
public void levelTraversal(AVLTreeNode root){
Queue queue = new LinkedList<>();
if(root != null){
queue.offer(root);
while(!queue.isEmpty()){
AVLTreeNode node = queue.poll();
System.out.print(node.getData() + " ");
AVLTreeNode left = node.getLeft();
if(left != null){
queue.offer(left);
}
AVLTreeNode right = node.getRight();
if(right != null){
queue.offer(right);
}
}
}
}
//递归遍历 前序
public void preTraversal(AVLTreeNode node){
if(node == null){
return;
}else{
System.out.print(node.getData() + " ");
preTraversal(node.getLeft());
preTraversal(node.getRight());
}
}
//递归遍历 中序
public void inTraversal(AVLTreeNode node){
if(node == null){
return;
}else{
inTraversal(node.getLeft());
System.out.print(node.getData() + " ");
inTraversal(node.getRight());
}
}
//递归遍历 后序
public void postTraversal(AVLTreeNode node){
if(node == null){
return;
}else{
postTraversal(node.getLeft());
postTraversal(node.getRight());
System.out.print(node.getData() + " ");
}
}
//插入节点
public AVLTreeNode insertTreeNode(int data){
if(root == null){
//根节点为空
root = new AVLTreeNode(data);
return root;
}else{
//用栈保存遍历的节点位置,后续依次弹出对节点进行旋转调整以保持二叉树的平衡
Stack stack = new Stack<>();
//判断是插入左右位置
boolean isLeft = false;
AVLTreeNode current = root;
AVLTreeNode parent = null;
while(current != null){
stack.push(current);
parent = current;
if(current.getData() > data){
current = current.getLeft();
isLeft = true;
}else{
current = current.getRight();
isLeft = false;
}
}
//循环结束则说明找到插入位置
AVLTreeNode node = new AVLTreeNode(data);
if(isLeft){
parent.setLeft(node);
}else{
parent.setRight(node);
}
//对遍历的节点进行旋转调整
while(!stack.isEmpty()){
current = stack.pop();
if(stack.isEmpty()){
parent = null;
}else{
parent = stack.peek();
}
//对节点进行旋转调整
rotate(current, parent);
}
return node;
}
}
/**
* 删除节点
* @param data
* @return
*/
public AVLTreeNode deleteNode(int data){
if(root == null){
return null;
}else{
//保存遍历节点,以后续对节点进行旋转调整
Stack stack = new Stack<>();
AVLTreeNode current = root;
AVLTreeNode parent = null;
boolean isLeft = false;
while(current != null && current.getData() != data){
stack.push(current);
parent = current;
if(current.getData() > data){
current = current.getLeft();
isLeft = true;
}else{
current = current.getRight();
isLeft = false;
}
}
if(current == null){
//找不到对应节点
return null;
}else{
if(current.getLeft() != null && current.getRight() != null){
//存在左右子树
//找到最小中序后继
AVLTreeNode minNode = finMinInNode(current);
minNode.setLeft(current.getLeft());
minNode.setRight(current.getRight());
if(parent == null){
root = minNode;
}else{
if(isLeft){
parent.setLeft(minNode);
}else{
parent.setRight(minNode);
}
//对替换的节点进行旋转调整
rotate(minNode, parent);
}
}else if(current.getLeft() != null){
//存在左子树
if(parent == null){
root = current.getLeft();
}else{
if(isLeft){
parent.setLeft(current.getLeft());
}else{
parent.setRight(current.getLeft());
}
}
}else if(current.getRight() != null){
//存在右子树
if(parent == null){
root = current.getRight();
}else{
if(isLeft){
parent.setLeft(current.getRight());
}else{
parent.setRight(current.getRight());
}
}
}else{
//叶子节点
if(parent == null){
root = null;
return current;
}else{
if(isLeft){
parent.setLeft(null);
}else{
parent.setRight(null);
}
}
}
//平衡遍历节点
if(stack.isEmpty()){
//删除的是根节点
//平衡替换的节点
rotate(root, parent);
}else{
while(!stack.isEmpty()){
AVLTreeNode pop = stack.pop();
if(!stack.isEmpty()){
parent = stack.peek();
}else{
parent = null;
}
rotate(pop, parent);
}
}
return current;
}
}
}
/**
* 找到最小中序后继
* 若找到对应节点,删除该节点,找的过程保存遍历的节点,找到对各个节点进行旋转调整保持平衡
* @param current
* @return
*/
public AVLTreeNode finMinInNode(AVLTreeNode current) {
//保存遍历节点
Stack stack = new Stack<>();
AVLTreeNode node = current.getRight();
AVLTreeNode preNode = current;
//一直向左遍历
while(node.getLeft() != null){
stack.push(node);
preNode = node;
node = node.getLeft();
}
if(node == current.getRight()){
//当前节点的最小中序后继节点是该节点的右节点,不需要进行调整
current.setRight(node.getRight());
}else{
preNode.setLeft(node.getRight());
while(!stack.isEmpty()){
AVLTreeNode pop = stack.pop();
if(stack.isEmpty()){
preNode = current;
}else{
preNode = stack.peek();
}
rotate(pop, preNode);
}
}
return node;
}
/**
* 对指定结点进行调整
* @param current
* @param parent
*/
public void rotate(AVLTreeNode current, AVLTreeNode parent) {
//在判断平衡因子之前,先对当前结点更新高度
current.setHeight(Math.max(getHeight(current.getLeft()), getHeight(current.getRight())) + 1);
//得到该节点的平衡因子
int balanceFactor = getbalance(current);
//对于LL和LR型旋转,只要不是LL型,其他的都可以看做是LR型
//在这里是为了防止发生:结点的平衡因子是2,其孩子结点的平衡因子出现0的情况
//RR与RL也是类似的
if(balanceFactor == 2){
//左子树
if(getbalance(current.getLeft()) == 1){
//LL
rotateLL(current, parent);
}else{
//LR
rotateLR(current, parent);
}
}else if(balanceFactor == -2){
//右子树
if(getbalance(current.getRight()) == -1){
//RR
rotateRR(current, parent);
}else{
//RL
rotateRL(current, parent);
}
}
}
public int getHeight(AVLTreeNode node){
if(node == null){
return 0;
}else{
return node.getHeight();
}
}
/**
* RL型旋转
* @param current
* @param parent
*/
public void rotateRL(AVLTreeNode current, AVLTreeNode parent) {
AVLTreeNode right = current.getRight();
AVLTreeNode rightLeft = right.getLeft();
right.setLeft(rightLeft.getRight());
rightLeft.setRight(right);
current.setRight(rightLeft.getLeft());
rightLeft.setLeft(current);
if(parent != null){
if(parent.getLeft() == current){
parent.setLeft(rightLeft);
}else{
parent.setRight(rightLeft);
}
}else{
root = rightLeft;
}
//更新高度
right.setHeight(Math.max(getHeight(right.getLeft()), getHeight(right.getRight())) + 1);
current.setHeight(Math.max(getHeight(current.getLeft()), getHeight(current.getRight())) + 1);
rightLeft.setHeight(Math.max(current.getHeight(), right.getHeight()) + 1);
}
/**
* RR型旋转
* @param current
* @param parent
*/
public void rotateRR(AVLTreeNode current, AVLTreeNode parent) {
AVLTreeNode right = current.getRight();
current.setRight(right.getLeft());
right.setLeft(current);
if(parent != null){
if(parent.getLeft() == current){
parent.setLeft(right);
}else{
parent.setRight(right);
}
}else{
root = right;
}
//更新高度
current.setHeight(Math.max(getHeight(current.getLeft()), getHeight(current.getRight())) + 1);
right.setHeight(Math.max(current.getHeight(), getHeight(right.getRight())) + 1);
}
/**
* LL型旋转
* @param current
* @param parent
*/
public void rotateLL(AVLTreeNode current, AVLTreeNode parent) {
AVLTreeNode left = current.getLeft();
current.setLeft(left.getRight());
left.setRight(current);
if(parent != null){
if(parent.getLeft() == current){
parent.setLeft(left);
}else{
parent.setRight(left);
}
}else{
root = left;
}
//更新高度
current.setHeight(Math.max(getHeight(current.getLeft()), getHeight(current.getRight())) + 1);
left.setHeight(Math.max(getHeight(left.getLeft()), current.getHeight()) + 1);
}
/**
* LR型旋转
* @param current
* @param parent
*/
public void rotateLR(AVLTreeNode current, AVLTreeNode parent) {
AVLTreeNode left = current.getLeft();
AVLTreeNode lefeRightNode = left.getRight();
left.setRight(lefeRightNode.getLeft());
lefeRightNode.setLeft(left);
current.setLeft(lefeRightNode.getRight());
lefeRightNode.setRight(current);
if(parent != null){
if(parent.getLeft() == current){
parent.setLeft(lefeRightNode);
}else{
parent.setRight(lefeRightNode);
}
}else{
root = lefeRightNode;
}
//更新高度
left.setHeight(Math.max(getHeight(left.getLeft()), getHeight(left.getRight())) + 1);
current.setHeight(Math.max(getHeight(current.getLeft()), getHeight(current.getRight())) + 1);
lefeRightNode.setHeight(Math.max(left.getHeight(), current.getHeight()) + 1);
}
/**
* 获取平衡因子
* @param current
* @return 左子树高度-右子树高度
*/
public int getbalance(AVLTreeNode current) {
if(current == null){
return 0;
}
AVLTreeNode left = current.getLeft();
AVLTreeNode right = current.getRight();
if(left == null && right == null){
return 0;
}else if(left != null && right == null){
//右子树为空
return left.getHeight();
}else if(right != null && left == null){
//左子树为空
return right.getHeight() * (-1);
}else{
//左右子树不为空
return left.getHeight() - right.getHeight();
}
}
}
参考地址:
Java 代码实现平衡二叉树(插入、删除、查找、遍历操作)_spcoder的博客-CSDN博客_java平衡二叉树删除
平衡二叉树详解 通俗易懂_邓嘉文Jarvan的博客-CSDN博客_平衡二叉树