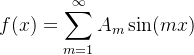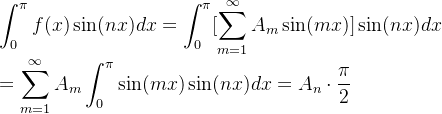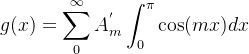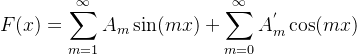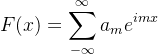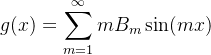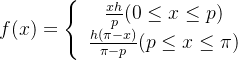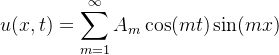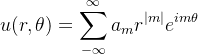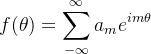Fourier分析导论——第1章——Fourier分析的起源(E.M. Stein & R. Shakarchi)
第 1 章 Fourier分析的起源
(The Genesis of Fourier Analysis)
Regarding the researches of d'Alembert and Euler could
one not add that if they knew this expansion, they
made but a very imperfect use of it. They were both
persuaded that an arbitrary and discontinuous function
could never be resolved in series of this kind, and
it does not even seem that anyone had developed a
constant in cosines of multiple arcs, the first problem
which I had to solve in the theory of heat
(关于 d'Alembert(达朗贝尔) 和 Euler(欧拉) 的研究,没有人能补充说,即使他们知道这个展开,他们也只是非常不完善地使用了它。他们都被这种观点说服了,即,一个任意且不连续的函数永远不能用这种级数来求解,而且,甚至似乎没有人开发出多弧余弦的常数表示,这是我在热分析理论中必须解决的第一个问题。)
------------------------------------------------------------------------------J.Fourier[fúriə], 1808-9
起初,是振动弦(vibrating string)的问题,后来是热流研究问题,导致了Fourier分析的发展。支配这些不同物理现象的定律由两个不同的偏微分方程表示,波动方程(wave function)和热传导方程(heat function),这些方程用Fourier级数求解。
在这里,我们想从详细描述这些思想的发展开始。我们将首先在振动弦问题的背景下,从振动弦的问题出发,我们将分三个步骤进行。首先,我们描述了几个物理概念(凭经验的),这些概念激发了对我们的研究具有重要意义的相应数学思想。它们是:简谐运动所隐含的函数 ![]() 、
、![]() 和
和 ![]() 的作用;从驻波现象中导出的变量分离法用法;以及与音调叠加(superposition)相关的线性概念。接下来,我们推导出控制振动弦运动的偏微分方程。最后,我们将使用所了解的问题的物理属性(以数学方式表达)来求解方程。在最后一节中,我们使用相同的方法来研究热扩散问题。
的作用;从驻波现象中导出的变量分离法用法;以及与音调叠加(superposition)相关的线性概念。接下来,我们推导出控制振动弦运动的偏微分方程。最后,我们将使用所了解的问题的物理属性(以数学方式表达)来求解方程。在最后一节中,我们使用相同的方法来研究热扩散问题。
鉴于本章的介绍属性和涵盖的主题,我们的介绍不能基于纯粹的数学推理。相反,它通过合理性论证进行,旨在为后续章节中的进一步严格分析提供动力。不耐烦的读者希望立即从主题的定理开始,可能更愿意直接跳过本章而进入下一章。
1.1 振动弦问题(The vibrating string)
该问题涉及研究一根固定在其端点并允许自由振动的弦的运动。我们想到了物理系统,例如乐器的弦。正如我们上面提到的进行步骤,我们首先基于我们的研究,简要描述几种可观察到的物理现象。这些物理现象分别是:
![]() 简谐运动(simple harmonic motion)(即,简单的谐振运动),
简谐运动(simple harmonic motion)(即,简单的谐振运动),
![]() 驻波和行波(standing and traveling wave),
驻波和行波(standing and traveling wave),
![]() 谐波和音调的叠加(harmonics and superposition of tones)。
谐波和音调的叠加(harmonics and superposition of tones)。
了解这些现象背后的经验事实将激发我们研究振动弦的数学方法。
(译注:谐,指“和谐”,这种波的特点是,这种波分解之后存在多个不同频率的波,但是,他们都存在一个共同的基波频率,这些不同的波的频率都是这个基频率的整数倍,这样的波表现在音乐中,就是“和声”,而不是杂乱无章的“嘈杂声”,因此取名为“谐波”。)
(译注:“简谐运动”的“简”为何意?因为这种运动的波形是按正弦或者余弦规律变化的,是机械振动中“最简单的”一类。)
简谐运动
简谐振动描述了最基本的振荡系统(oscillatory system)(称为简谐振荡器(oscillator))的行为,因此自然而然地成为振动研究的起点。考虑一个连接到水平弹簧(spring)的滑块(mass){m},水平弹簧本身连接到固定墙壁上,并假设系统位于无摩擦表面上。选择一个轴,其原点与静止时滑块中心重合(即弹簧既未拉伸也未压缩),如图 1 所示。当滑块从其初始平衡位置(equilibrium)移动然后释放时,它将进行简谐运动。一旦我们找到控制滑块运动的微分方程,就可以用数学工具来描述这种运动。
--------------------------------------------------图1 简谐振荡器-----------------------------------------------------
用 y(t ) 表示滑块在 t 时刻的位移(displacement),我们假设弹簧是理想型,即在满足胡克定律(Hooke's law)的这种意义上是理想的:弹簧施加在滑块上的恢复力 F 由 F = -ky(t)给出。这里的 k > 0 ,是一个已知的物理论,称为弹簧常量(spring constant)。应用牛顿定律(力=滑块质量 m × 加速度),我们得到
![]() ,
,
其中,我们使用记号 y’’ 表示 y 针对于 t 的二阶导数(the second derivative)(译注:一阶导数的数学意义上表示“曲线切线的斜率”,二阶导数的在数学意义表示物体的“加速度”,可以由导数的定义推导出)。由于 ![]() , 这个二阶常微分方程就化成了
, 这个二阶常微分方程就化成了
(1) ![]() 。
。
方程(1)的通解由 ![]() 给出,其中,a 和 b 是常量。显然,此形式的所有函数都求解方程(1),练习 6 概略地给出了这些是该微分方程唯一(二次可微)解的证明。
给出,其中,a 和 b 是常量。显然,此形式的所有函数都求解方程(1),练习 6 概略地给出了这些是该微分方程唯一(二次可微)解的证明。
在以上针对 y(t) 的表达式中,c 是已经常量,但是 a 和 b 可以是任意实数。为了确定方程的特别解(译注:简称“特解”),鉴于 a 和 b 是两个未知常量,我们必须施加两个初始条件。例如,假如我们已知 y (0)和 y’(0),滑块的初始位置和速度,则这个物理问题的解是唯一的且由下式给出
读者可以很容易地验证,存在常量 A > 0 以及 φ∈ℝ (译注:手写体双线字母,表示实数)使得
![]() 。
。
由于上面给出的物理解释,我们可以称 ![]() 为运动的“振幅(amplitude)”,称 c 为其“自然频率(natural frequency)”,称 φ 为其“相位(phase)”(唯一地确定 2π 的最小整数倍),以及称 2π/c为运动的“周期(period)”。
为运动的“振幅(amplitude)”,称 c 为其“自然频率(natural frequency)”,称 φ 为其“相位(phase)”(唯一地确定 2π 的最小整数倍),以及称 2π/c为运动的“周期(period)”。
A cos(ct - φ) 的典型图形如图2所示,图形展示了通过平移和拉伸(或收缩) cos(t)的常规图形获得的波浪状图案。
![]()
----------------------------------------------------图2 A cos(ct - φ)的图形----------------------------------------------
我们对简谐运动的检验做了两个观察。首先是最基本的振荡系统即简谐运动的数学描述涉及最基本的三角函数cos(t)和sin(t)。在接下来的内容中,重要的是要回忆这些函数与复数之间的联系,如欧拉恒等式(Euler's identity) ![]() 中给出的那样。第二个观察是简谐运动由两个初始条件确定为时间的函数,一个确定位置,另一个确定速度(例如,在时间 t = 0 时指定)。正如我们将在下面看到的,更一般的振荡系统都具有此属性。
中给出的那样。第二个观察是简谐运动由两个初始条件确定为时间的函数,一个确定位置,另一个确定速度(例如,在时间 t = 0 时指定)。正如我们将在下面看到的,更一般的振荡系统都具有此属性。
驻波和行波(standing and traveling wave)
事实证明,可以根据一维波运动来观察振动的弦。在这里,我们想描述两种适用于简单图形表示的运动。
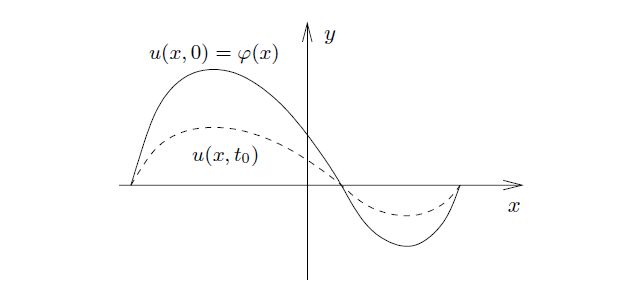
第一种,我们考虑驻波(standing wave)。存在如图 3 所示的用图形 y = u(x,t)所描述的按时间进行的波状运动。换句话说,存在一个表示 t = 0 时刻波的初始轮郭(profile) y = φ(x),以及一个取决于时间 t 的放大系数 ψ(t),使得
![]() 。
。
驻波特征展现了“变量分离”的思想,后面我们会再次回到这个主题。
------------------------------------图3 不同时刻的驻波图:t = 0 时刻和 ![]() 时刻----------------------
时刻----------------------
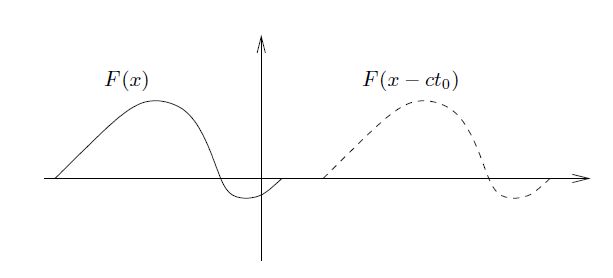
第二种,称为行波(traveling wave)。描述它相当简单:存在一个初始轮廓 F(x) 使得在 t = 0 时刻 ![]() 。随着时间 t 的演进,这个轮廓向右侧平移 ct 个单位,其中,c 是一个正整数,即,
。随着时间 t 的演进,这个轮廓向右侧平移 ct 个单位,其中,c 是一个正整数,即,
![]() 。
。
在图形上,这种图形如图 4 所描述。
---------------------------------图4 不同时刻的行波图:t = 0 时刻和 ![]() 时刻--------------------------
时刻--------------------------
因为其在时间上以速度(velocity)c 移动,这个常量 c 表示波的速度。函数 ![]() 表示向右平移的一维行波。类似地,
表示向右平移的一维行波。类似地,![]() 表示向左平移的一维行波。
表示向左平移的一维行波。
谐波和音调的叠加(harmonics and superposition of tones)
我们要提到的最后一个物理观察(现在不讨论任何细节)是音乐家自远古以来就已经意识到的。它是谐波(harmonics)或泛音(overtones)的存在。纯音(pure tones)伴随着泛音的组合,泛音主要决定乐器的音色(timbre)(或“tone color”)。音调的组合或叠加的思想在数学上是通过线性的基本概念实现的,我们将在下面看到。
我们现在将注意力转向我们的主要问题,即描述振动弦的运动。首先,我们推导出波动方程,即控制弦运动的偏微分方程。
1.1.1 波动方程的引出
设想,将一个均匀的弦(homogeneous string)置于(x,y)平面的,并在 x = 0 和 x = L 之间沿着 x 轴拉伸。如果将其设置为振动,则其位移 ![]() 是 x 和 t 的函数,目标是推导出控制该函数的微分方程。
是 x 和 t 的函数,目标是推导出控制该函数的微分方程。
为此,我们将其想象为弦被细分为足够大的沿 x 轴均匀分布的 N 块(我们将其视为一个个单独的质点),因此,第 n 个质点其 x 轴坐标为 ![]() 。因此,我们应该将这个振动弦想像成一个具有 n 个质点的复杂系统,每个质点仅在垂直方向振动;然而,与我们前面考虑的简谐振荡器不同的是,每个质点都将通过弦的张力将其振荡与其直接相邻的质点联系起来。
。因此,我们应该将这个振动弦想像成一个具有 n 个质点的复杂系统,每个质点仅在垂直方向振动;然而,与我们前面考虑的简谐振荡器不同的是,每个质点都将通过弦的张力将其振荡与其直接相邻的质点联系起来。
然后,我们令 ![]() , 并注意到,
, 并注意到,![]() 。假如,我们假设弦具有常量的密度 ρ > 0 ,则分配 ρh 的质量到每个质点是合理的。按照牛顿定律,则
。假如,我们假设弦具有常量的密度 ρ > 0 ,则分配 ρh 的质量到每个质点是合理的。按照牛顿定律,则 ![]() 为施加到每个质点上的作用力。现在,我们作简单的假设,这个施加的作用力是受附近两个质点的影响,即,具有
为施加到每个质点上的作用力。现在,我们作简单的假设,这个施加的作用力是受附近两个质点的影响,即,具有 ![]() 坐标的质点是受其前面质点
坐标的质点是受其前面质点 ![]() 和其后面质点
和其后面质点 ![]() 的影响(如图 5 所示)。我们进一步假设,来自右侧的这第 n 个质点的这个力(或张力)与
的影响(如图 5 所示)。我们进一步假设,来自右侧的这第 n 个质点的这个力(或张力)与 ![]() 成正比,其中,h 是
成正比,其中,h 是 ![]() 和
和 ![]() 之间的间距;因此,我们可以将这个张力写成
之间的间距;因此,我们可以将这个张力写成
其中,τ 是一个常量,等于弦的张力系数。也存在一个类似的来自左侧的力,它是
![]() 。
。
---------------------------------------图5 作为离散质点系统的振动弦-----------------------------------------
总而言之,将这些力相加可以得到振荡器 ![]() 之间所需的关系,即,
之间所需的关系,即,
(2) ![]() 。
。
在另一方面,用上面选择的记法,我们看到
![]() 。
。
此外,对于任意合理的函数 F(x)(即,其具有连续的二阶导数),我们有
因此,在(2) 中除以 h, 并令 h 趋近于0(即,N 趋近于无穷大), 我们可以推断出
或
这种关系称为一维波动方程(one-dimensional wave equation),或者,更为简洁地,称为波动方程(wave equation)。这个原因后面为更加明了,系数 c > 0 称为运动的速度(velocity)。关于这个波动方程,我们做一个重要且简单的数学评论。这与尺度(scaling)有关,或者,用物理学的语言来说,是与“单位变化(change of units)”有关。即,我们可以将坐标 x 看成是 x = aX ,其中,a 是一个合适的正常量。现在,根据新的坐标X,区间 0 ≤ x ≤ L 就转换成了 0 ≤ X ≤ L/ a 。类似地,我们可以将时间坐标替换成 t = bT ,其中,b 是另一个合适的正常量。假如我们令 U (X,T) = u(x , t ),则
类似地,对于 t 的导数也如此。因此,如果我们选择恰当的 a 和 b ,我们可以将一维波动方程转换成
这与将速度 c 设置为 1 等效。此外,我们可以自由地将区间从 0 ≤ x ≤ L 转换到 0 ≤ x ≤ π 。(我们将会看到,在很多场合,选择 π 都是方便的。) 所有这些,都可以通过代入 a = L /π 和 b = L /(cπ) 来实现。很显然,一旦我们求解了变换后的新方程,我们可以通过对变量进行逆向改变来回到原来的方程。因此,我们不用考虑在区间[0,π ]上给出具有速度 c = 1 波动方程,从而牺牲方程的通用性。
1.1.2 波动方程的解
推导出振动弦的方程后,我们现在解释两种求解方法:
![]() 行波法,
行波法,
![]() 驻波叠加法。
驻波叠加法。
虽然第一种方法非常简单且优雅,但它并没有直接给出对问题的全面洞察;第二种方法做到了这一点,而且具有广泛的适用性。人们最初认为,第二种方法仅适用于弦的初始位置和速度本身作为驻波叠加给出的简单情况。然而,作为 Fourier 思想的成果,很明显,对于所有初始条件,该问题都可以用任何一种方式解决。
行波法
与前面一样,为了简化问题,我们假设 c = 1 ,L = π ,我们期望求解的方程就转换成了
关键的观测结果如下:假如 F 是任意的二次微分函数,则 u(x,t) = F(x + t) 和 u(x,t) = F(x - t) 则作为微分方程的解。对此的验证留作一个简单的微分练习题。注意到,u(x,t) = F(x - t)在 t = 0 时刻的图像只是 F 的图像,而在 t = 1 时刻的图像是 F 向右平移 1 个单位后的图像。因此,我们认识到 F(x - t) 是一个以速度 1 向右传输的行波。类似地,u(x,t) = F(x + t)是一个以速度 1 向左传输的行波。这些运动如图 6 所示。
-----------------------------------------------图6 向两个方向传输的波形图----------------------------------------
我们对声调及其组合的讨论引导我们观察到,波动方程是线性的。这意味着假如 u(x,t ) 和 v(x,t ) 是特解,则 α u(x,t ) + β v(x,t ) 也是其特解,其中 α 和 β 是任意常量。因此,我们可以叠加两个沿相反方向传输的波,从而得到,只要 F(x) 和 G(x) 是二次可微函数,则
![]()
是波动方程的一个解。事实上,现在我们展示了其所有解都采用了这种形式。
我们暂且去掉 0 ≤ x ≤ π 这个假设条件,并假设 u 对于所有实数 x 和 t 而言都是作为方程解的二次可微函数。考虑以下新的变量组 ξ = x + t ,η = x - t ,并定义 v(ξ , η) = u(x,t) 。变量转换公式表明 v 满足
对这个关系进行二次积分就得出 v(ξ , η) = F(ξ) + G(η),这意味着,对于某些函数 F 和 G ,有
![]() 。
。
现在, 我们必须将这个问题与我们原来的问题联系起来,即,弦运动的物理问题。此前,我们加入了约束条件 0 ≤ x ≤ π ,弦的初始形状 u(x,0) = f (x),并且弦具有固定端点,即对于所有的 t ,u(x,0) = u(π, t ) = 0 。为了使用上面的简单观察结果,我们首先将 f 延拓到整个实数域 ℝ ,按奇函数延拓到闭区间 [-π, π ]上(注:在集合 U 上 上的奇函数定义为:假如,对于任意 x ∈ U ,都有– x ∈ U,且 f (-x)= - f (x),则 f(x) 是奇函数,如果有 f (-x)= f (x),则 f(x) 是偶函数),则其在 x 上具有以 2π 为周期的周期性(注:如果对于定义域 ℝ 上的所有 x ,都有 f (x + ω)= f (x ),则称 f (x )具有以 ω 为周期的周期性),对于 u (x,t )也类似,使其成为了我们问题的解。则这个扩展的 u 成为了整个 ℝ 上波动方程的解,以及所有 x ∈ ℝ 的 u(x,0) = f (x) 的解。因此,根据 ![]() ,我们令 t = 0,求得
,我们令 t = 0,求得
![]() 。
。
因为很多 F 和 G 选项都满足恒等式,这体现了在 u 上施加的另外一个初始条件(类似于简谐运动情况下的两个初始条件),即,我们用 g(x) 表示的弦的初始速度:
显然,其中的 g(0) = g(π) = 0 。此外,我们首先将 g 延拓到 ℝ,按奇函数延拓到闭区间[-π, π]上,则 g 是具有以 2π 为周期的周期性。现在,这两个位置和速度的初始条件转换为下列系统:
微分第一个方程并将其微分结果加到第二个方程,我们得到
![]() 。
。
按照类似的消项法,得到
![]() ,
,
因此,存在常量 ![]() 和
和 ![]() 使得
使得
和
因为 ![]() ,我们推出
,我们推出 ![]() , 因此,最终我们的具有给定初始条件的波动方程的解采用下面的形式
, 因此,最终我们的具有给定初始条件的波动方程的解采用下面的形式
这种形式的解称为达朗贝尔公式(d'Alembert's formula)。注意,我们为 f 和 g 选择的扩展保证了弦始终具有固定端,即,对于所有的 t ,有 ![]() 。
。
最后,依次说明一下。上面所做的从 t ≥ 0 到 x ∈ ℝ,然后再到 t ≥ 0 的这个过程,表现出波动方程的时间反演(time reversal)特性。换句话说,对于 t ≥ 0,波动方程的一个解 u ,会导出一个定义在负时间 t < 0 上的解 ![]() ,仅需置
,仅需置 ![]() ,这是在 t ↦ -t 转换下波动方程的不变性得出的事实。这种状况与热传导方程的情况完全不一样。
,这是在 t ↦ -t 转换下波动方程的不变性得出的事实。这种状况与热传导方程的情况完全不一样。
驻波叠加法
我们转向第二种求解波动方程的方法,它基于我们先前物理观察的两个基本结论。通过对驻波的考虑,我们被引向寻找形为 φ(x)ψ(t) 的波动方程的特解。这个例程在其他情况下同样有效(例如,在热传导方程的情况下),称为变量分离法(separation of variables)并构造了称为纯音的解。则根据波动方程的线性性,我们可以期望将这些纯音组合成更为复杂的组合音。将这种思想进一步推广,最终我们可以期望根据这些特解的和来表述波动方程的通解。
注意到,在一方面,波动方程仅涉及对 x 的微分,而在另一方面,又只涉及对 t 的微分。这种观察结果提供了按形式 φ(x)ψ(t) (即,“分离变量”)寻找方程解的另外一个理由——将困难的偏微分方程降低为相对简单的普通微分方程系统的期望。在波动方程的情况下,u 具有以上的变量分离形式,我们得到
![]() ,
,
因此
在这儿,关键的观察点在于,左侧的表达式仅取决于变量 t,右侧的表达式仅取决于变量x。仅当两侧都是一个常量时(比如,等于λ)才会发生这种情况。因此,波动方程简化为下列式子
在上面的系统中,我们将注意力放在第一个方式上。至此,读者就会认出我们在研究简谐运动时得到的方程。注意,我们必须只考虑当 λ < 0 时的这种情况,因为,当 λ ≥ 0 时,解 ψ 不会随时间的变化而体现出摆动。因此,我们可以写成 ![]() ,则方程的解由下式给出
,则方程的解由下式给出
![]() 。
。
类似地,我们求得(3)中第二个方程的解是
![]() 。
。
现在,我们考虑将条件 x = 0 和 x = π 加到弦上。这就转换成 φ(0) = φ(π) ,其反过来又给出 ![]() 且
且 ![]() ,则 m 必定为整数。假如 m = 0,解同样消失,而假如 m ≤ -1,我们可以重命名常量,并归结为 m ≥ 1 这种情况,因为函数 sin(y)是奇函数,而 cos(y) 是偶函数。最后,我们触及这个猜想——对于任意m ≥ 1,有函数
,则 m 必定为整数。假如 m = 0,解同样消失,而假如 m ≤ -1,我们可以重命名常量,并归结为 m ≥ 1 这种情况,因为函数 sin(y)是奇函数,而 cos(y) 是偶函数。最后,我们触及这个猜想——对于任意m ≥ 1,有函数
![]() ,
,
这是我们认识的驻波(standing wave),它是波动方程的一个解。注意,在上面的论证中,我们分为 φ 和 ψ ,它们有时候会消失,因此,实际上必须人为手动检测驻波 ![]() 是否可以求解方程。这种直接的计算方法留作读者习题。
是否可以求解方程。这种直接的计算方法留作读者习题。
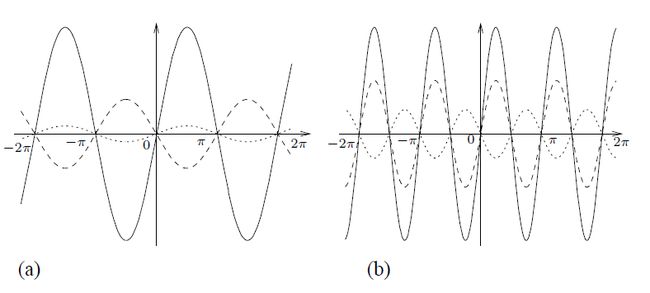
在进一步分析波动方程之前,我暂停一下,详细地讨论一下驻波。这个术语可以从观察 ![]() 对于每一个固定时刻 t 的图像而加以理解。首先假设 m = 1,且取 u(x,t ) = cos(t) sin(x) 。则图 7 (a) 给出了针对不同的 t 值 u 的图像。
对于每一个固定时刻 t 的图像而加以理解。首先假设 m = 1,且取 u(x,t ) = cos(t) sin(x) 。则图 7 (a) 给出了针对不同的 t 值 u 的图像。
---------------------------------图7 在不同的时刻的基音(a)和泛间(b)的波形图--------------------------------
m = 1 的情况对应基音(fundamental tone)或者振动弦的第一个谐波(the first harmonic)(译注:即基波,将泛音分解后的众多倍频波中频率最低的那一个波,其它的波其频率都是这个基频率的整数倍)。
现在,我们取 m = 1 ,看看 u(x,t ) = cos(2t) sin(2x) 。这对应第一个泛音(the first overtone)或第二个谐波(the second harmonic),这个运动的波形图如图 7 (b) 所示,注意,对所有的 t 而言,u(π/2,t ) = 0。这些在时间上保持静止的点,称为波节点(nodes),而其运动具有最大振幅的点称为反波节点(anti-nodes)。
对于更大的 m 值,我们会得到更多的泛音或谐波。注意,随着 m 的增加,频率也增加,并且周期 2π/m 递减。因此,基音比起泛音,具有更低的频率。
现在,我们回到原来讨论的问题。我们记得,假如 u 和 v 是方程的解,则 αu + βv 对于任何常量 α 和 β 而言,也构成方程的解,从这个意义上讲,波动方程是线性的。这就允许我们使用驻波 ![]() 的线性组合构造更多的解。这种技术称为叠加(superposition), 将我们引向我们最终的猜想——波动方程的解
的线性组合构造更多的解。这种技术称为叠加(superposition), 将我们引向我们最终的猜想——波动方程的解
注意,上面的和是无限的,因此,就出现了收敛性的问题。但因为到目前为止,我们大部分的论证都是公式化的,现在我们不担心收敛性的问题。
假设上面的表达式给出了波动方程的所有解。则假如我们要求弦在 t = 0 时刻的初始位置由闭区间[0, π ]上的函数 f 的形状给出,其中,显然有 f(0) = f(π) = 0,我们有u(x,0) = f(x),因此
因为弦的初始形状可以是任意合理的函数 f,我们一定会提下面的基本问题:
已经闭区间[0, π ]上的函数 f (其中,f (0) = f (π) = 0),我们可以求得系数 ![]()
使得
这个问题说起来轻松,但是本书随后的两章,为了精确地阐述并尝试回答这个问题,我们要付出很多的努力。这是开启Fourier分析研究的基本问题。
如果展开式(5)成立,一个简单的观察可以让我们猜出给出 ![]() 的公式。事实上,我们用 sin(nx) 乘以等式两侧并在区间[0, π ]对其进行积分;正式计算,我们得到
的公式。事实上,我们用 sin(nx) 乘以等式两侧并在区间[0, π ]对其进行积分;正式计算,我们得到
其中,我们用到这个事实
因此,我们猜测 ![]() ,称为 f 的第 n 项 Fourier正弦系数,其表达式为
,称为 f 的第 n 项 Fourier正弦系数,其表达式为
(6) ![]() 。
。
在后面,我们会回到这个公式以及其相关公式。
可以将闭区间[0, π ]上的Fourier正弦级数问题转换为闭区间[-π, π ] 上的更通用的问题。是否我们可以在闭区间[0, π ]上根据正弦级数来表示函数 f,则如果我们按奇函数延拓到闭区间 [-π, π ]上,是否这个延拓也成立。类似地,有人会问这样的问题,是否在闭区间[-π, π]上的一个偶函数 g(x)可以表示成一个余弦级数,即
更一般地,因为闭区间 [- π, π ] 上任意函数 F 都可以表示成 f + g,其中 f 是奇函数,g是偶函数(例如,取 ![]() ,我们可能会问题,是否可以将 F 写成
,我们可能会问题,是否可以将 F 写成
或者,应用 Euler 恒等式 ![]() ,我们可以期望 F 采用形式
,我们可以期望 F 采用形式
通过类比(6),我们可以利用这个事实
可以看出期望出现的结果是
![]() 。
。
这个量 ![]() 称为函数 F 的第 n 项Fourier系数(Fourier Coefficient)。
称为函数 F 的第 n 项Fourier系数(Fourier Coefficient)。
我们现在可以重新表述(reformulate)上面提出的问题:
问题:给予闭区间[-π, π]上的任意合理的函数 F,且具有如上定义的Fourier系数,下面这个公式
根据复数指数,这个问题的公式正是我们将在下文中使用最多的格式。
Joseph Fourier (1768-1830)是第一位认为“任意”函数 F 都可以用某个级数(7)给出的数学家。换句话说,他的中心思想在于,任意函数都是基本三角函数 sin(mx) 和 cos(mx) 的线性组合(可能是无穷项),其中 m 覆盖整个整数(注:后来,Dirichlet 证明了一般函数类都可以用Fourier级数表示)。尽管这种思想隐含在诸多早期的工作中,但是Fourier坚信他的前辈们没有认识到这一点,他将这种函数表示应用到他的热扩散(heat diffusion)研究中;这便是“Fourier分析(Fourier Analysis)”这个主题的发端。这个学科,首次发展是为了解决某个物理问题,被证实在数学和其它领域也有广泛的应用,我们后面将会介绍这些应用。(译注:Fourier对热量从高温区域流向低温区域的方式特别感兴趣。牛顿已经研究过这个问题,并发现物体的冷却速度(温度下降)与其周围环境的温度差
成正比。然而,牛顿冷却定律仅适用于温度的时间变化率,而不适用于它的空间变化率或梯度。后一个量取决于许多因素:物体的热导率、几何形状和边界上的初始温度分布。要处理这个问题,必须使用连续统的分析工具,特别是偏微分方程)(partial differential equations)。Fourier 认为,要求解这样一个方程,必须将初始温度分布表示为无穷多个正弦项和余弦项的总和——三角级数(trigonometric series)或 Fourier 级数(Fourier series)。)
我们回到波动方程,为了正确地公式化这个问题,我们必须施加两个初始条件,正如我们在简谐运动和行波方面的经验所表明的那样。这两个初始条件赋予了弦的初始位置和速度。即,我们要求 u 满足以下微分方程及两个条件,即,
![]() 和
和 ![]() ,
,
其中,f 和 g 是预置(pre-assigned)函数,注意,这与(4)是一致的,即,都要求 f 和 g 可分别表示为
1.1.3 例释:弹拔弦(the plucked string)
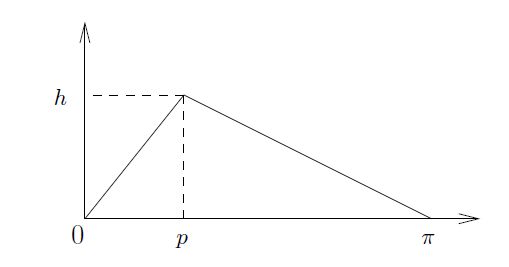
我们现在将我们的推理结论应用于弹拨弦的特定问题。为简单起见,我们选择的单位要确保弦取闭区间[0, π],且满足 c = 1 的波动方程。假定弦在点 p 处被弹拨的高度为 h,且 0 < p < π ;这是初始位置。即,我们把我们的初始位置看成是由以下式子给出的三角形状
其形状如图 8 所示。
-----------------------------------------------------图8 弹拔弦的初始位置-----------------------------------------
同样,我们也选择一个初始速度 g(x)等于 0 。则我们可以计算出 f 的Fourier系数,假设在(5)之前提出的问题的答案是正的,我们就得到
因此,有
并注意到,这个级数绝对收敛。这个解也可以按照行波来表示。事实上
此处,f (x)定义在满足如下条件的所有 x 上:首先,将 f 按奇函数延拓至闭区间[-π, π],然后将 f 按照 2π 为周期的周期性延拓至整个实数线,即,对于所有的整数 k,都有 f (x + 2πk) = f (x)。
注意到,鉴于恒等式
![]() ,
,
则等式(8)成立,即意味着等式(9)成立。
作为最后的评述,我们应该注意到这个问题的解的一个不令人满意的方面,然而这是事物的本质。由于弹拨弦的初始数据 f (x) 不是两次连续可微的,因此函数 u(由 (9) 给出)也不是。因此 u 并不是波动方程的真正解:虽然 u(x ,t) 确实表示弹拨弦的位置,但它不满足我们要求解的偏微分方程!只有当我们意识到 u 确实解了方程,但在适当的广义意义上,这种事态才可能被正确理解。要更好地理解这种现象,就需要掌握与之相关的“弱解(weak solutions)”和“分布理论(distributions)”研究的思想。 我们只会在后面的第三卷和第四卷中考虑这些主题。
1.2 热传导方程(The heat equation)
我们现在按照与波动方程相同的框架来讨论热扩散(heat diffusion)问题。首先,我们推导出时间相关的(time-dependent)热传导方程,然后研究圆盘(disc)中的稳态热传导方程(steady-state heat function),这将我们带回到基本问题(7)。
1.2.1 热传导方程的推导
考虑一个无限大的金属平面,我们将其作为二维平面 ![]() 的模型,并假设给予我们一个 t = 0 时刻的初始热分布。 t 时刻点(x,y)的温度用 u(x,y, t)表示。
的模型,并假设给予我们一个 t = 0 时刻的初始热分布。 t 时刻点(x,y)的温度用 u(x,y, t)表示。
考虑一个中心位于点 ![]() 且边长为 h 的正方形 S,其两边分别平行于坐标轴,如图 9 所示。在 t 时刻 S 中的热能总量由下式给出
且边长为 h 的正方形 S,其两边分别平行于坐标轴,如图 9 所示。在 t 时刻 S 中的热能总量由下式给出
其中,σ > 0 是一个常量,称为物质的比热(specific heat,全称“specific heat capacity”,又称“比热容量”,是单位质量物质的热容量,即单位质量物体改变单位温度时吸收或放出的热量)。因此, 流入 S 的热量是
上式近似等于
因为 S 的面积是 ![]() 。现在,我们应用牛顿冷却定律,它指出,热量以某个正比于温度差值的比率从温度高的一端流向温度低的一端,即,梯度率。
。现在,我们应用牛顿冷却定律,它指出,热量以某个正比于温度差值的比率从温度高的一端流向温度低的一端,即,梯度率。
------------------------------------------------------图 9 流过小正方形的热量---------------------------------------
因此,通过右侧垂直侧的热量是
其中 ![]() 是材料电导率。对于其它侧的类似论证表明,流过正方形 S 的总热量由下式给出
是材料电导率。对于其它侧的类似论证表明,流过正方形 S 的总热量由下式给出
应用中值定理(mean value theorem)并令 h 趋近于0,我们求得
这就是时间相关的热传导方程(time-dependent heat equation),通常简称热传导方程(heat equation)。
1.2.2 圆盘中的稳态热传导方程
经过很长一段时间后,不再有热交换,因此系统达到热平衡(thermal equilibrium),并且 ![]() 。在这种情况下,热传导方程简化为稳态热传导方程
。在这种情况下,热传导方程简化为稳态热传导方程
运算符 ![]() 在数学和物理中是如此重要,以至于通常将其作为一个整体缩写为 Δ(译注:这是希腊字母的第4个字母的大写,读音[/ˈdɛltə/])并取了一个专用名字:拉普拉期运算符(Laplace)或拉氏算子( Laplacian)。因此,稳态热传导方程可以写为
在数学和物理中是如此重要,以至于通常将其作为一个整体缩写为 Δ(译注:这是希腊字母的第4个字母的大写,读音[/ˈdɛltə/])并取了一个专用名字:拉普拉期运算符(Laplace)或拉氏算子( Laplacian)。因此,稳态热传导方程可以写为
Δ u = 0 ,
并且,这个方程的解称为调和函数(harmonic functions)(或简谐函数、谐函数)。
考虑平面上的单位圆盘
![]() ,
,
它的边界是单位圆 C。用坐标 (r ,θ) 表示,r ≥ 0 且 0 ≤ θ < 2π ,我们有
![]() 和
和 ![]() 。
。
这个问题,通常称为 Dirichlet 问题(Dirichlet problem)(单位圆盘上的拉氏算子),是以基于 C 上的函数 u = f 为边界条件的单位圆盘的方程的解。这对应于在圆周上固定一个预置的温度分布,等待很长时间,然后再看圆盘内部的温度分布。虽然变量分离法对等式 (10) 很有用,但困难在于边界条件不容易用直角坐标表示。因为这种边界条件最适合使用极坐标(r ,θ)描述,即 u(1,θ) = f(θ),我们以极坐标 (r ,θ) 重写拉氏算子。一种链式法则的应用:
在上式中,我们在等式两边分别乘以 ![]() , 因为 Δu = 0,我们得到
, 因为 Δu = 0,我们得到
将这些变量分离,观察形如 ![]() 的方程解,我们求得
的方程解,我们求得
因为等式的两边取决于不同的变量,它们一定等于某个常量,比如,等于 λ 。于是,我们得到下列的等式
因为 G 一定是一个以 2π 为周期的周期函数,这意味着 λ ≥ 0 ,以及(正如前面所见) ![]() ,其中 m 是一个整数;因此,
,其中 m 是一个整数;因此,
![]() 。
。
应用 Euler 恒等式 ![]() ,根据复数指数重写 G 为
,根据复数指数重写 G 为
![]() 。
。
其中,![]() 且 m ≠ 0,方程中,F 的两个简单解分别是
且 m ≠ 0,方程中,F 的两个简单解分别是 ![]() 和
和 ![]() 。假如 m = 0, 则
。假如 m = 0, 则 ![]() 和
和 ![]() 是其两个解。假如 m > 0 ,我们注意到
是其两个解。假如 m > 0 ,我们注意到 ![]() 随着 r 趋近于 0 无边界地增大 ,因此 F(r)G(θ)在其原点是无界的;当 m = 0 且
随着 r 趋近于 0 无边界地增大 ,因此 F(r)G(θ)在其原点是无界的;当 m = 0 且 ![]() 时也会发生这种情况。我们拒绝这些解,因为它们与我们的直觉相悖。因此,只剩下下面的特解
时也会发生这种情况。我们拒绝这些解,因为它们与我们的直觉相悖。因此,只剩下下面的特解
![]() , m ∈ ℤ (译注:双线字母 Z 表示整数集)
, m ∈ ℤ (译注:双线字母 Z 表示整数集)
现在,我们做出重要的观察,即,(10)是线性的。因此,与振动弦情况一样,我们可以叠加上面的特解以获得推定的通解
如果这个表达式给出稳态热传导方程的所有解,则我们应当具有的这个合理的函数 f 应为
![]() 。
。
因此,在这样的语境中,我们不禁又会问:给定闭区间[0,2π]上的函数 f ,且有 f (0) = f (2π),我们可以求得系数 ![]() 以使得
以使得
成立吗?
关于Fourier分析历史的说明
D'Alembert(1747 年)首先用行波法求解了振动弦的方程。一年后,Euler 详细阐述了这个解。 1753 年,D.Bernoulli 提出的解其所有意图和目的都是由 (4) 给出的Fourier级数,但 Euler 并不完全相信它的普遍性,因为只有当一个“任意”函数可以展开时,这在Fourier级数中才成立。D'Alembert和其他数学家也有怀疑。Fourier(1807年)在他对热传导方程的研究中改变了这种观点,他的执着信念和卓越的工作最终导致了其他数学家完全证明了一般函数都可以表示成Fourier级数。
内容来源:
<
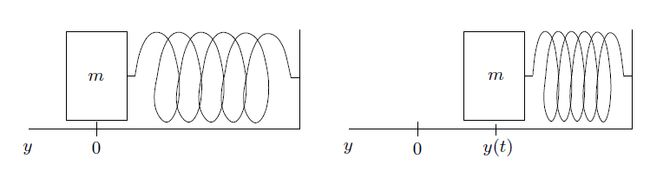

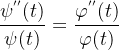
![\displaystyle u_{m}(x,t)=\sum_{m=1}^{\infty}[A_{m}\cos(mt)+B_{m}\sin(mt)]\sin(mx)](http://img.e-com-net.com/image/info8/0aac63756618496587865a76224eee0b.png)