线性表的定义和基本操作

线性表的定义和基本操作

一、线性表的定义

线性表（Linear List）是具有相同数据类型的n(n>=0)个数据元素的有限序列，其中n为表长，当n=0时线性表是一个空表。若用L命名线性表，则其一般表示为

L = (a1,a2,...,ai,ai+1,...,an)

ai是线性表中的“第i个”元素线性表中的位序

a1是表头元素；an是表尾元素。

除第一个元素外，每个元素有且仅有一个直接前驱；出最后一个元素外，每个元素有且仅有一个直接后继；

二、线性表的基本操作

InitList(&L)：初始化表。构造一个空的线性表L，分配内存空间。

DestroyList(&L)：销毁操作。销毁线性表，并释放线性表L所占有的内存空间。

ListInsert(&L,i,e)：插入操作。在表L中的第i个位序（位置）上插入制定元素e。

ListDelete(&L,i,&e)：删除操作。删除表L中第i个位序（位置）的元素，并用e返回删除元素的值。

LocateElem(L,e)：按值查找操作。在表L中查找具体给定关键字值的元素。

GetElem(L,i)：按位查找操作。获取表L中第i个位置的元素的值。

其他常用操作：

Length(L)：求表长操作。返回线性表L的长度，即L中数据元素的个数。

PrinList(L)：输出操作。按前后顺序输出线性表L的所有元素值。

Empty(L)：判空操作。若L为空表，则返回true，否则返回false。

Tips：

①对数据的操作（记忆思路）——创（Init）销（Destroy）、增（Insert）删（Delete）改（Alter）查（Query）

②C语言函数的定义

③实际开发中，可根据实际需求定义其他的基本操作

④函数名和参数的形式、命令都可改变

⑤什么时候需要传入“&”——对参数的修改结果需要“带回来”

三、初始化代码实践

1、顺序表静态分配

#include 
// 顺序表存储空间静态分配
#define MaxSize 10      // 定义最大长度
typedef int ElemType;   // int类型重命名为ElemType，方便后续调整
typedef struct{         // 定义结构体
    ElemType data[MaxSize];         // 用静态的数组存放数据元素
    ElemType length;                // 数组长度
}SqList;
void InitList(SqList &L){           // 初始化顺序表
    L.length=0;                     // 长度赋值,没有设置数据元素的默认值
}
int main() {
    SqList L;           // 声明一个顺序表
    InitList(L);    // 初始化顺序表
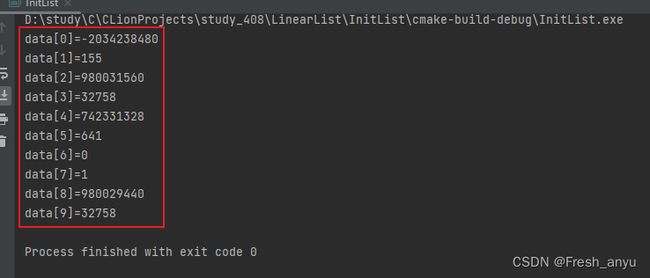
    for (int i = 0; i < MaxSize; i++) {
        // 尝试违规打印整个data数组
        printf("data[%d]=%d\n", i, L.data[i]);
    }
    return 0;
}

#include 
// 顺序表存储空间静态分配
#define MaxSize 10      // 定义最大长度
typedef int ElemType;   // int类型重命名为ElemType，方便后续调整
typedef struct{         // 定义结构体
    ElemType data[MaxSize];         // 用静态的数组存放数据元素
    ElemType length;                // 数组长度
}SqList;
void InitList(SqList &L){          // 初始化顺序表
    for(int i=0;i

2、顺序表动态分配

#include 
#include 
// 顺序表存储空间动态分配
#define InitSize 10      // 顺序表初始长度
typedef int ElemType;   // int类型重命名为ElemType，方便后续调整
typedef struct{         // 定义结构体
    ElemType *data;     // 用静态的数组存放数据元素
    ElemType MaxSize;   // 顺序表最大容量
    ElemType length;    // 顺序表数据长度
}SqList;
void InitList(SqList &L){           // 初始化顺序表
    // 用malloc函数申请一片连续的存储空间
    L.data = (ElemType *) malloc(InitSize * sizeof(ElemType));
    L.MaxSize = InitSize;
    L.length = 0;
}
void IncreaseSize(SqList &L, ElemType len){
    ElemType *p=L.data;
    L.data = (int *) malloc((L.MaxSize + len) * sizeof(ElemType));
    for (ElemType i = 0; i < L.length; i++) {
        L.data[i]=p[i];     // 将数据复制到新区域
    }
    L.MaxSize=L.MaxSize+len;    // 顺序表最大长度增加len
    free(p);            // 释放原来的内存空间
}
int main() {
    SqList L;           // 声明一个顺序表
    InitList(L);    // 初始化顺序表
    IncreaseSize(L, 5);
    return 0;
}

3、特点

随机访问：即可以在O(1)时间内找到第i个元素。

存储密度高：每个节点只存储数据元素。

扩展容量不方便：即便采取动态分配的方式实现，拓展长度的时间复杂度也比较高。

插入、删除操作不方便：需要移动大量的元素。

四、插入和删除

1、顺序表插入实践

#include 

#define MaxSize 10      // 指定大小
typedef int ElemType;
typedef struct{
    ElemType data[MaxSize];
    ElemType length;
}SqList;

bool InsertList(SqList &L, ElemType position, ElemType element){
    if (position < 1 || position > L.length + 1) {      // 判断插入是否合理
        return false;
    }
    if (L.length >= MaxSize) {          // 判断插入是否合理
        return false;
    }
    for (ElemType i = L.length; i >= position; i--) {   // 循环从最后一位开始，到插入的位序，减减
        L.data[i] = L.data[i-1];        // 将前一位值向后移一位
    }
    L.data[position-1] = element;       // 插入的位置附上要插入的值，注意数组下标和位序是相差一位的
    L.length++;                         // 插入一个元素之后，数组的长度是要加1
    return true;
}

void PrintList(SqList L){
    for (ElemType i = 0; i < L.length; i++) {
        printf("data[%d]=%d\n",i,L.data[i]);
    }
}
int main() {
    SqList L;   // 初始化
    for (ElemType i = 0; i < 6; i++) {      // 数组赋值
        L.data[i]=i*2;
    }
    L.length=6;
    bool ret;
    ret = InsertList(L, 6, 20); // 调用插入
    if (ret) {          // 判断是否正常插入
        printf("insert element success\n");
        PrintList(L);
    } else {
        printf("insert element failed\n");
    }
    return 0;
}

插入操作的时间复杂度

最好情况：新元素插入到表尾，按照以上例子为插入位序为6的位置，不需要移动元素，循环0次，最好时间复杂度=O(1)

最坏情况：新元素插入到表头，需要将原有的n个元素全部都向后移动，循环n次，最坏时间复杂度=O(n)

平均情况：假设新元素插入到任何一个位置的概率相同，即i=1,2,3,…,length+1的概率都是
$$p=\frac{1}{n+1}$$
i=1,循环n次，i=2，循环n-1，…，i=n+1，循环0次
$$平均循环次数=np+(n-1)p-(n-2)p+...+1.p=\frac{n(n+1)}{2}\cdot \frac{1}{n+1}=\frac{n}{2}$$
平均时间复杂度=O(n)

2、顺序表删除实践

#include 

#define MaxSize 10      // 指定大小
typedef int ElemType;
typedef struct{
    ElemType data[MaxSize];
    ElemType length;
}SqList;

bool DeleteList(SqList &L, ElemType position, ElemType &element){
    if (position < 1 || position > L.length + 1) {      // 判断删除是否合理
        return false;
    }
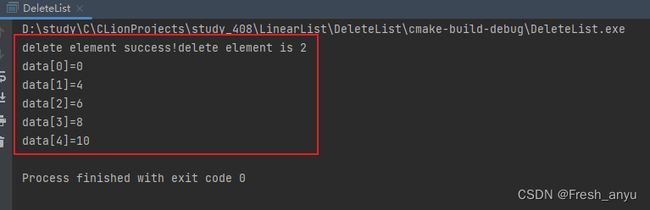
    element = L.data[position-1];       // 删除的数据，注意数组的下标和位序的关系
    for (ElemType i = position; i 

最好情况：删除表尾元素，不需要移动元素，循环0次，最好时间复杂度=O(1)

最坏情况：删除表头元素，需要将后续n-1个元素全部向前移动，循环n-1次，最坏时间复杂度=O(n)

平均情况：假设删除任何一个元素的概率相同，即i=1,2,3,…,length+1的概率都是
$$p=\frac{1}{n}$$
i=1,循环n-1次，i=2，循环n-2，…，i=n，循环0次
$$平均循环次数=(n-1)p-(n-2)p+...+1.p=\frac{n(n-1)}{2}\cdot \frac{1}{n}=\frac{n-1}{2}$$
平均时间复杂度=O(n)

3、顺序表查询实践

#include 

// 静态分配
#define MaxSize 10		// 定义最大长度

typedef int Element;

typedef struct{
    Element data[MaxSize];		// 用静态的“数组”存放数据元素
    int length;
}SqList;
	
int GetList(SqList L,int position){		// 查询该位序的值
    return L.data[position - 1];		// 位序和数组下标少一位
}

int LocateList(SqList L,int num){		// 查询值在数据哪个位序
    for (int i = 0; i < L.length; i++) {
        if (L.data[i] == num) {
            return i+1;					// 返回位序和数组下标相差一位
        }
    }
}
int main() {
    SqList L;
    for (int i = 0; i < 5; i++) {
        L.data[i] = i*2;
    }
    L.length=5;
    int ret;
    ret = GetList(L, 3);
    printf("Get List num is %d\n", ret);

    ret = LocateList(L,4);
    printf("Locate List position is %d\n", ret);
    return 0;
}

#include 
#include 
// 动态分配
#define InitSize 10

typedef int Element;

typedef struct{
    Element *data;
    int MaxSize;
    int length;
}SqList;

void InitList(SqList &L){               // 初始化
    L.data = (int *) malloc(InitSize*sizeof(int));
    L.MaxSize = InitSize;
    L.length = 0;
}

int GetList(SqList L,int position){		// 查询该位序的值
    return L.data[position - 1];		// 位序和数组下标少一位
}

int LocateList(SqList L,int num){		// 查询值在数据哪个位序
    for (int i = 0; i < L.length; i++) {
        if (L.data[i] == num) {
            return i+1;					// 返回位序和数组下标相差一位
        }
    }
}
int main() {
    SqList L;
    InitList(L);
    for (int i = 0; i < 5; i++) {
        L.data[i] = i*2;
    }
    L.length=5;
    int ret;
    ret = GetList(L, 3);
    printf("Get List num is %d\n", ret);

    ret = LocateList(L,4);
    printf("Locate List position is %d\n", ret);
    return 0;
}

时间复杂度：

按位查找：O(1)

按值查找：最好时间复杂度：O(1)，在第一个位置

​ 最坏时间复杂度：O(n)，在最后一个位置

​ 平均时间复杂度：O(n)，目标元素在每个位置的概率相同
$$O=(1+2+...+n)\frac{1}{n}=\frac{n(n+1)}{2}\cdot \frac{1}{n}=\frac{n+1}{2}=O(n)$$