剖析数据在内存中的存储及有无符号数的整形提升

目录

前言

一、整形数据在内存中的存储

1. char类型

2. int类型

二、浮点数类型

存储格式详解

以 int* 访问 float 变量

以 float* 访问 int 变量

总结

---

前言

        在计算机科学和数据处理领域，了解数据在内存中的存储方式对于理解计算机系统的工作原理至关重要。数据的存储方式直接影响其表示范围、精度和对计算机资源的利用。此外，了解有无符号数的整形提升也是至关重要的，因为它涉及到数据的有效表示范围和对计算结果的影响。在本篇博客中，我们将深入剖析数据在内存中的存储方式，重点关注整形数据（如 char 和 int）以及浮点数数据（如 float）的存储格式。我们将详细讨论每种类型在内存中的表示方式，并探讨有无符号数对整形提升的影响。此外，我们还将比较整形数据和浮点数数据在二进制编码方面的差异，以及使用指针在不同类型之间进行访问的实验验证。

        希望这篇博客文章能够帮助读者深入了解数据在内存中的存储方式，并对有无符号数的整形提升有更清晰的认识。

---

一、整形数据在内存中的存储

1. char类型

        首先来看一段代码，用于打印有无符号char类型存储数的结果：

void test1()
{
	char a = -1;
	signed char b = -1;
	unsigned char c = -1;
	printf("a=%d,b=%d,c=%d\n", a, b, c);
}

运行结果：

（注：上面代码运行环境为VS2022的x64得到此运行结果）

由于C语言标准并没有规定char类型一定归属于signed或unsigned，但是大多数编译器仍然认为char类型为有符号类型，即 signed char = char 。

为什么上面变量c的结果是255而不是-1呢，这就涉及到unsigned和signed类型可存储的数据范围是不同的，在内存中存储允许的有效边界值是不同的，遵循下面的存储规则：

可以看到unsigned char取值范围为0~255，而signed char取值范围为-128~127，所以对unsigned char类型变量赋值-1时，相当于从0开始逆时针步行一个单位，值即为255。

再来一个案例：

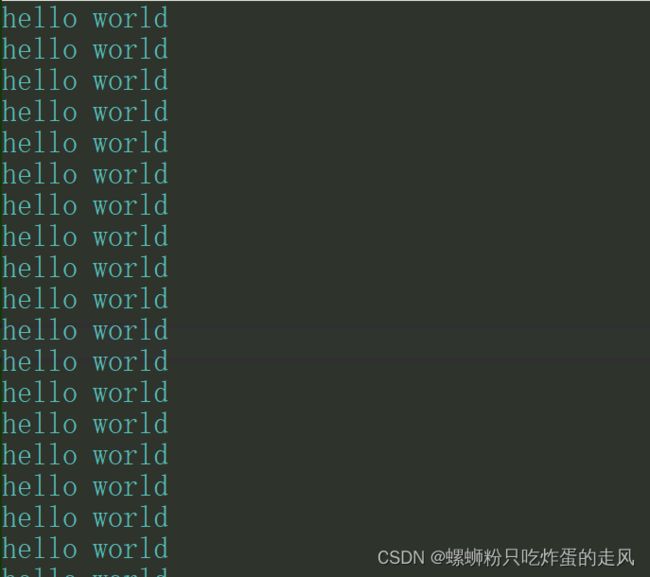
void test7()
{
	unsigned char i = 0;
	for (i = 0; i <= 255; i++)
	{
		printf("hello world\n");
		Sleep(500);
	}
}

运行结果：

程序崩溃，因为执行的是死循环，对于无符号类型变量的值，永远不会小于0，所以循环条件始终符合。

接着看：

void test6()
{
	char a[1000];
	int i;
	for (i = 0; i < 1000; i++)
	{
		a[i] = -1 - i;
	}
	printf("%d\n", strlen(a));
}

先试着判断上面代码的运行逻辑，再想想输出结果，结果如下：

        为什么结果是255呢？  我们首先要明确strlen()函数的实现逻辑，只有当遍历字符数组到'\0'时才停止，反观上面代码循环部分，a[i] 的值从-1开始沿着signed char虚拟环逆时针流转赋值，当 a[i] 达-128后，下次循环时将会以127的值传给 a[i+1] ，接着递减为0后再重复整个过程，直到循环执行次数达到1000次。

继续一段代码，分析其结果：

void test3()
{
	//char :-128~127
	char a = 128;
    printf("%d\n", a);
	printf("%u\n", a);
}

（注：上面代码中的%u表示以无符号十进制类型输出a的值）

不用感觉char类型最多只能放127，这里怎么赋值超出允许范围了，但是正如你所愿，挤是挤了点，不影响赋值给变量的过程。

运行结果：

下面这个数具体是多少呢，用计算器转换看看：

我们看看为什么转换后会出现这么大的值：

//char :-128~127
char a = 128;
// 00000000000000000000000010000000 原(反、补)码
// 10000000 截断
// 有符号整形提升
// 11111111111111111111111110000000 有符号补码
// 11111111111111111111111101111111 有符号反码
// 10000000000000000000000010000000 有符号原码（输出结果）
// 无符号整形提升
// 00000000000000000000000010000000 无符号补码
// 00000000000000000000000001111111 无符号反码
// 11111111111111111111111110000000 无符号原码（输出结果）

为何会有截断，为何有无符号数输出结果会不同，分别涉及到了截断存储和整型提升的知识，可以想象char类型亦或者short类型实际归属于整形，所以它们内存中存储的方式和int类型是一致的，只不过它两分别只可以占1和2字节，对应二进制比特位即为8位和16位，int类型即占32位。值128的补码在赋值给char类型元素时，只能保留后8位，即 10000000 。当需要以有符号或无符号数进行输出时，就会涉及到整形提升，而有无符号数有着各自的整数提升规则，从而出现了有无符号输出结果不同的情况。

同时，整形提升方式有以下注意点：

• 提升后的二进制编码为补码，并非原码
• 有符号正数（提升前十进制数为正数）和无符号提升（接收提升后变量类型为无符号类型）时，补码前面所有位补0；
• 有符号负数（提升前十进制数为负数），补码前面所有位补1

2. int类型

积累上面char类型讲解的知识，这部分自然会显得得心应手了，来看一段代码：

void test4()
{
	int i = -20;
	// 10000000000000000000000000010100 原码
	// 11111111111111111111111111101011 反码
	// 11111111111111111111111111101100 补码
	unsigned int j = 10;
	// 00000000000000000000000000001010 原(反、补)码
	printf("%d\n", i + j);
	// 补码加和
	// 11111111111111111111111111110110 补码
	// 11111111111111111111111111110101 反码
	// 10000000000000000000000000001010 原码（打印输出）
}

代码注释中直接给出编译器对整形和无符号整形加和运算的逻辑法则，即先同时转换为补码在加和运算，打印输出时再将所得补码转换为原码即可，运行结果如下：

接着看一段代码：

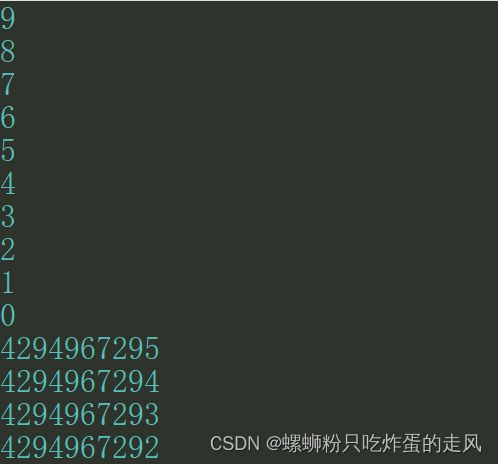
void test5()
{
	unsigned int i;
	for (i = 9; i >= 0; i--)
	{
		Sleep(500);   // 设定输出延迟 便于观察结果
		printf("%u\n", i);
	}
}

运行结果：

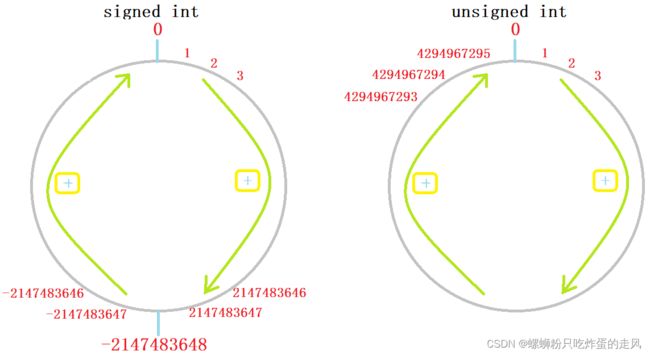
为何会出现 i 的值等于0，接着递减一次后 i 的值反而很大很大，没错，因为它是无符号整数，是不存在负数情况的。正如上面画的 unsigned char 类型数值可以取到的范围是始终大于0的，我们同样可以作出 (signed) int 和 unsigned int 类型的取值环形图。

 

这样一来，对上面代码运行结果将会有更加深刻的认识。

二、浮点数类型

首先同样地推测以下代码的运行结果：

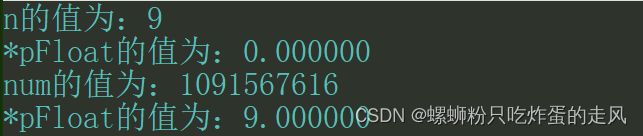
int n = 9;
float* pFloat = (float*)&n;
printf("n的值为：%d\n", n);
printf("*pFloat的值为：%f\n", *pFloat);
*pFloat = 9.0;
printf("num的值为：%d\n", n);
printf("*pFloat的值为：%f\n", *pFloat);

运行结果：

        我们看到1、4行输出是比较理想的，但是2、3行出现了意料之外的结果，究其原因还是因为整形和浮点型数据在内存中的存储格式是不同的，整形中可以看作每个不同高位具有不同的权重，这里不再赘述，浮点型的存储格式是异于整形的，因为浮点数类型还涉及到小数部分的存储，由于float类型和int类型都只占4个字节，所以浮点型选取类似科学计数法的方式存储数据，具体存储格式如下：

根据国际标准IEEE（电气和电子工程协会） 754，任意一个二进制浮点数V可以表示成下面的形式：

• (-1)^S * M * 2^E
• (-1)^S表示符号位，当S=0，V为正数；当S=1，V为负数。
• M表示有效数字，大于等于1，小于2。
• 2^E表示指数位。

举例来说：
十进制的5.0，写成二进制是101.0 ，相当于1.01×2^2 。
那么，按照上面V的格式，可以得出S=0，M=1.01，E=2。
十进制的-5.0，写成二进制是-101.0 ，相当于-1.01×2^2 。那么，S=1，M=1.01，E=2。

所以具体存储流程是将十进制转换为二进制后，再改写为2为底幂次表示的科学计数法形式。

存储格式详解

IEEE 754规定：

1. 对于32位的浮点数，最高的1位是符号位S，接着8位是指数E，剩下的23位为有效数字M

2. 对于64位的浮点数，最高的1位是符号位S，接着11位是指数E，剩下的52位为有效数字M

不同位内存分配占用示例画图如下：

32位浮点数

64位浮点数

因为科学计数法允许指数为负数，而这里E内编码为无符号数，所以具体存储的指数值E是在实际指数值 E' 的基础上加 127<32位浮点数>（或1023<64位浮点数>），将其表示为：

32位：

64位：

例如我们将要初始化 float a = 5.5; 时，实际上存入的二进制码如下：

float a = 5.5;
// 101.1
// (-1)^0 * 1.011 * 2^2
// S = 0       (1)
// M = 1.011   (23)      M -> .011     只存小数部分
// E = 2       (8)     E+127 = 129
// 存储顺序为 S->E->M
// 0 10000001 01100000000000000000000
// 0100 0000   1011 0000   0000 0000   0000 0000  二进制4间距等分直接转化为一位十六进制数
// 40          b0          00          00

需要注意的是，M只存小数部分是因为取值为M的取值范围为[1,2)，所以当我们描述浮点数在内存中存储的二进制编码时要注意M部分的 23位<32位浮点数>（或52位<64位浮点数>）仅仅存储科学计数法底数的小数部分。

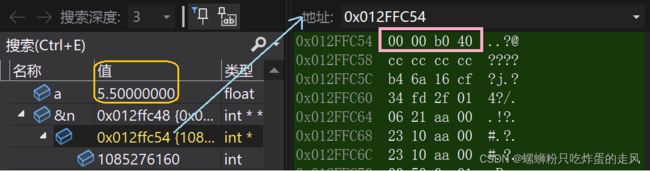
通过上面的分析，我们已经清晰认识到存浮点数入内存的具体方式，接着打开运行的内存窗口观察上面代码中变量a的存储值是否和预想的一致：

可以看到绿色窗口中的值为 00 00 b0 40 和上面代码中注释部分推测的一致，顺序相反仅仅因为机器为小端机器，低位存储在低地址，高位存储在高地址，仅此而已。

以 int* 访问 float 变量

如果我们用读取 int 类型的方式读取该 float 类型变量a的二进制编码，那么将会是一个非常大的值，程序内读取打印：

代码如下：

float a = 5.5;
// 0 10000001 01100000000000000000000
// 0100 0000   1011 0000   0000 0000   0000 0000  二进制4间距等分直接转化为一位十六进制数
// 40          b0          00          00
int* n = (int*)&a;
printf("%d\n", *n);

运行结果：

调试窗口：

通过上面调试不难发现，当我们利用整形指针指向 float 类型变量地址并解引用访问时，得到的数是将 float 类型变量二进制数直接按照整形二进制方式读取，所以出现运行结果：1085276160

计算器对结果转换后，确实对应内存窗口的十六进制值。

以 float* 访问 int 变量

执行下面代码：

int num = 999999999;
float* f_p = (float*)#
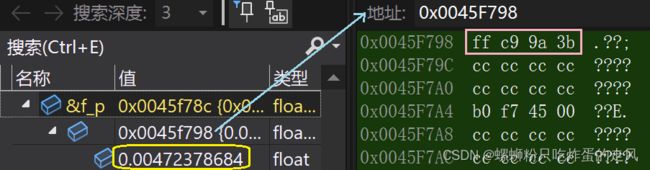
printf("%f\n", *f_p);

运行结果：

调试窗口：

当我们利用 float 类型指针指向 int 类型变量地址并解引用访问时，得到的数是将 int 类型变量二进制数拆分为 float 类型二进制存储方式（S->E->M）读取，所以出现运行结果：0.004724

计算器将整数转换为二进制编码：

下面给出以 float 二进制读取整数二进制分析部分：

int num = 999999999;
// 0011 1011  1001 1010  1100 1001  1111 1111
// 3b         9a         c9         ff
float* f_p = (float*)#
// 0    01110111    00110101100100111111111  float二进制
// S    E           M
// 将整数二进制看作存入的浮点型二进制，读取时E'需要减去127(或1023)
// 0    119(E'=-8)  1755647（M'= 1.1755647）  float科学计数法十进制
// (-1)^0 * 1.1755647 * 2^(-8)
// 1.1755647/256 = 0.004592

因为数字实在太小，所以允许机器运算存在误差，和控制台给出的结果0.004724大致相同。

E 中同时有1和0

另外我们在上面例子中 E 的表示部分同时存在0和1的数位，所以可以直接减去127（或1023）即可得到科学计数法中用于直接计算的 E' 值。对M值需要前面加上第一位的1，因为我们前面讲述过对 float 类型数进行存储时，有效数字位仅存储小数点以后的数字。

E全为0

这时，浮点数的指数E等于1-127（或者1-1023）即为真实值，
有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。这样做是为了表示±0，以及接近于0的很小的数字。

E全为1

这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）；

---

总结

        在本篇博客中，我们深入探讨了数据在内存中的存储方式，并重点关注了整形数据（如 char 和 int）以及浮点数数据（如 float）的存储格式。我们了解了每种类型在内存中的表示方式，并详细讨论了有无符号数对整形提升的影响。通过比较整形数据和浮点数数据的存储格式，我们发现它们在二进制编码方面存在差异。我们还进行了实验，使用指针在不同类型之间进行访问，验证了存储格式的不同之处。

        通过本篇博客，希望读者能够更好地理解数据在内存中的存储方式，并对有无符号数的整形提升有更清晰的认识。深入了解这些概念对于编程和数据处理非常重要，可以帮助我们更好地理解计算机系统的工作原理，并编写更高效和准确的代码。在今后的编程和数据处理中，我们应该注意数据的存储方式，特别是在进行类型转换和数据操作时。了解数据的存储格式和类型之间的转换规则，将有助于我们编写出更健壮和可靠的代码。